Clase 7 Redes neuronales (parte 1)

7.1 Introducción a redes neuronales

En la parte anterior, vimos cómo hacer más flexibles los métodos de regresión: la idea es construir entradas derivadas a partir de las variables originales, e incluirlas en el modelo de regresión. Este enfoque es bueno cuando tenemos relativamente pocas variables originales de entrada, y tenemos una idea de qué variables derivadas es buena idea incluir (por ejemplo, splines para una variable como edad, interacciones para variables importantes, etc). Sin embargo, si hay una gran cantidad de entradas, esta técnica puede ser prohibitiva en términos de cálculo y trabajo manual.

Por ejemplo, si tenemos unas 100 entradas numéricas, al crear todas las interacciones $x_i x_j$ y los cuadrados $x_i^2$ terminamos con unas 5150 variables. Para el problema de dígitos (256 entradas o pixeles) terminaríamos con unas 32 mil entradas adicionales. Aún cuando es posible regularizar, en estos casos suena más conveniente construir entradas derivadas a partir de los datos.

Para hacer esto, consideramos entradas $X_1, . . . , X_p$, y supongamos que tenemos un problema de clasificación binaria, con $G = 1$ o $G = 0$. Aunque hay muchas maneras de construir entradas derivadas, una manera simple sería construir $m$ nuevas entradas mediante:

\[a_k = h \left ( \theta_{k,0} + \sum_{j=1}^p \theta_{k,j}x_j \right)\]

para $k=1,\ldots, m$, donde $h$ es la función logística, y las $\theta$ son parámetros que seleccionaremos más tarde. La idea es hacer combinaciones lineales de variables transformadas.

Modelamos ahora la probabilidad de clase 1 con regresión logística, pero en lugar de usar las entradas originales X usamos las entradas derivadas $a_1, . . . , a_m$: \[p_1(x) = h \left ( \beta_0 + \sum_{j=1}^m \beta_ja_j \right)\]

Podemos representar este esquema con una red dirigida ($m=3$ variables derivadas):

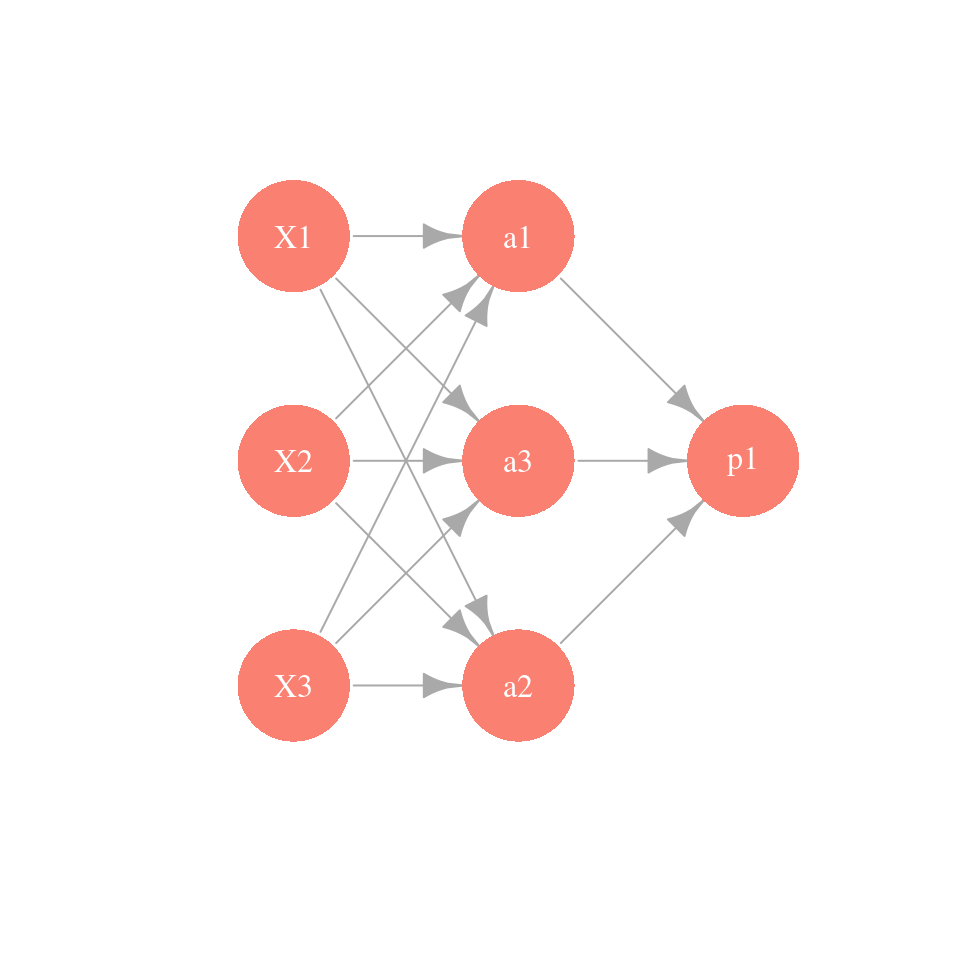
Observaciones:

¿Por qué usar $h$ para las entradas derivadas $a_k$? En primer lugar, nótese que si no transformamos con alguna función no lineal $h$, el modelo final $p_1$ para la probabilidad condicional es el mismo que el de regresión logística (combinaciones lineales de combinaciones lineales son combinaciones lineales). Sin embargo, al transformar con $h$, las $x_j$ contribuyen de manera no lineal a las entradas derivadas.
Las variables $a_k$ que se pueden obtener son similares (para una variable de entrada) a los I-splines que vimos en la parte anterior.
Es posible demostrar que si se crean suficientes entradas derivadas ($m$ es suficientemente grande), entonces la función $p_1(x)$ puede aproximar cualquier función continua. La función $h$ (que se llama función de activación no es especial: funciones continuas con forma similar a la sigmoide (logística) pueden usarse también (por ejemplo, arcotangente, o lineal rectificada). La idea es que cualquier función se puede aproximar mediante superposición de funciones tipo sigmoide (ver por ejemplo Cybenko 1989, Approximation by Superpositions of a Sigmoidal Function).

¿Cómo construyen entradas las redes neuronales?

Comencemos por un ejemplo simple de clasificación binaria con una sola entrada $x$. Supondremos que el modelo verdadero está dado por:

h <- function(x){
    1/(1 + exp(-x)) # es lo mismo que exp(x)/(1 + exp(x))
}
x <- seq(-2, 2, 0.1)
p <- h(2 - 3 * x^2) #probabilidad condicional de clase 1 (vs. 0)
set.seed(2805721)
x_1 <- runif(30, -2, 2)
g_1 <- rbinom(30, 1, h(2 - 3 * x_1^2))
datos <- data.frame(x_1, g_1)
dat_p <- data.frame(x, p)
g <- qplot(x, p, geom='line', colour="red")
g + geom_point(data = datos, aes(x = x_1, y = g_1), colour = 'red')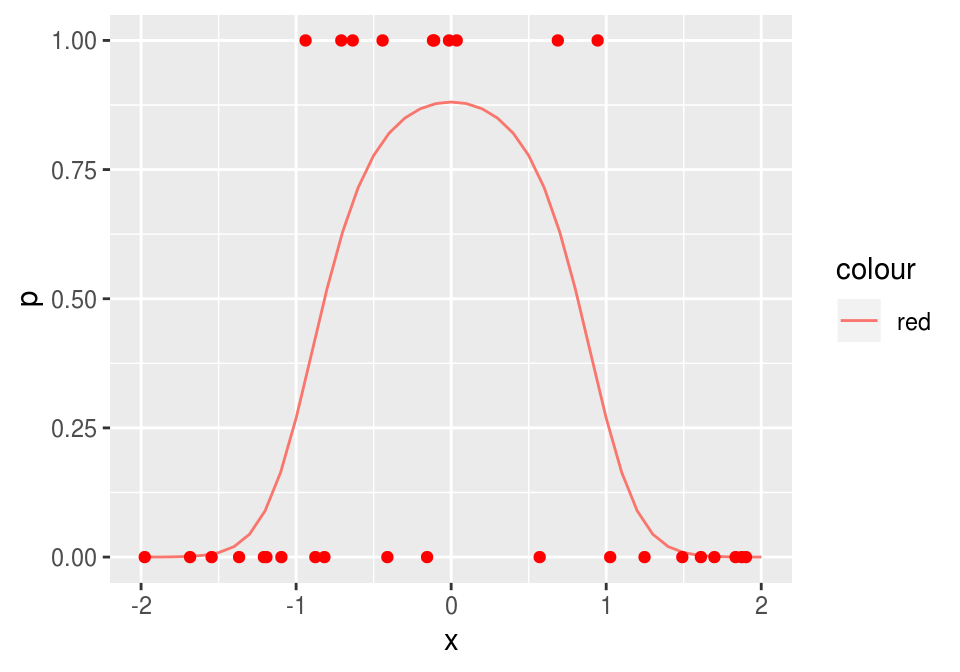

donde adicionalmente graficamos 30 datos simulados. Recordamos que queremos ajustar la curva roja, que da la probabilidad condicional de clase. Podríamos ajustar un modelo de regresión logística expandiendo manualmente el espacio de entradas agregando $x^2$, y obtendríamos un ajuste razonable. Pero la idea aquí es que podemos crear entradas derivadas de forma automática.

Supongamos entonces que pensamos crear dos entradas $a_1$ y $a_2$, funciones de $x_1$, y luego predecir $g.1$, la clase, en función de estas dos entradas. Por ejemplo, podríamos tomar:

donde hacemos una regresión logística para predecir $G$ mediante \[p_1(a) = h(\beta_0 + \beta_1a_1+\beta_2 a_2),\] $a_1$ y $a_2$ están dadas por \[a_1(x)=h(\beta_{1,0} + \beta_{1,1} x_1),\] \[a_2(x)=h(\beta_{2,0} + \beta_{2,1} x_1).\]

Por ejemplo, podríamos tomar

a_1 <- h( 1 + 2*x)  # 2(x+1/2)
a_2 <- h(-1 + 2*x)  # 2(x-1/2) # una es una versión desplazada de otra.

Las funciones $a_1$ y $a_2$ dependen de $x$ de la siguiente forma:

dat_a <- data_frame(x = x, a_1 = a_1, a_2 = a_2)
dat_a_2 <- dat_a %>% gather(variable, valor, a_1:a_2)
ggplot(dat_a_2, aes(x=x, y=valor, colour=variable, group=variable)) + geom_line()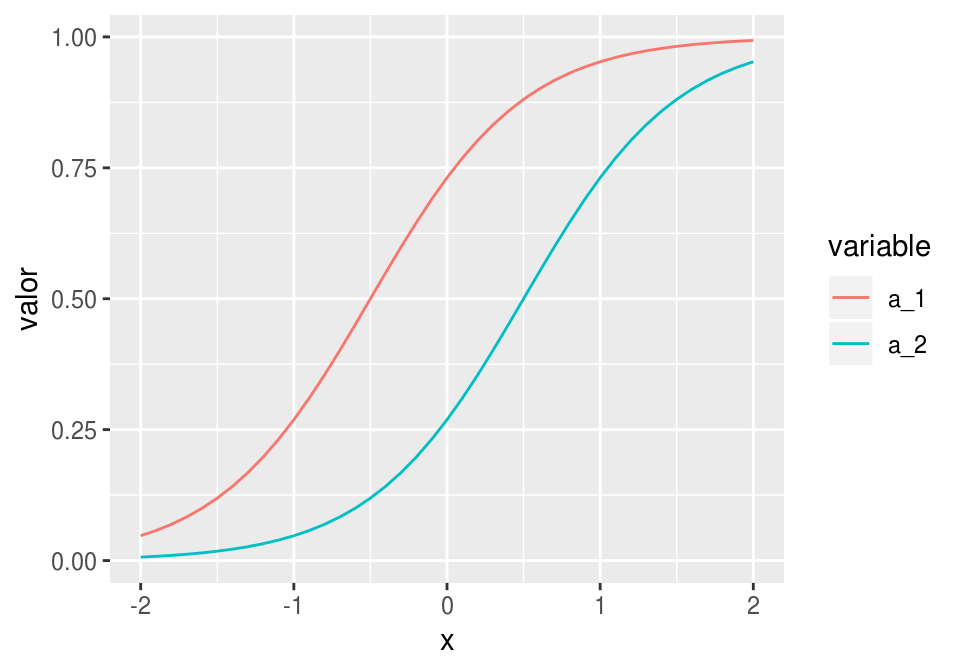

Si las escalamos y sumamos, obtenemos

dat_a <- data.frame(x=x, a_1 = -4 + 12 * a_1, a_2 = -12 * a_2, suma = -4 + 12 * a_1 - 12 * a_2)
dat_a_2 <- dat_a %>% gather(variable, valor, a_1:suma)
ggplot(dat_a_2, aes(x = x, y = valor, colour = variable, group = variable)) + geom_line()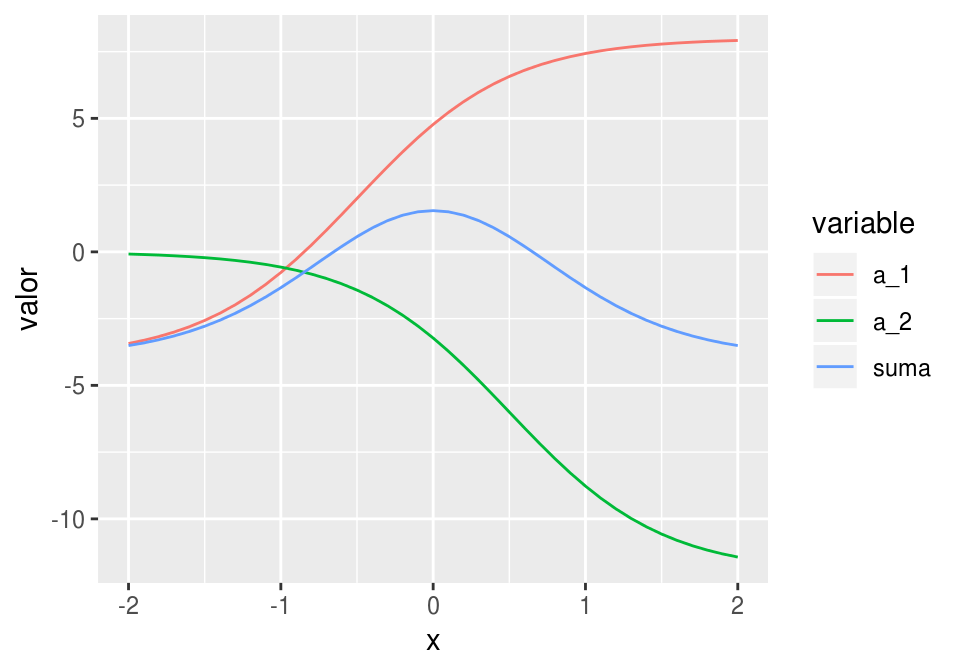

y finalmente, aplicando $h$:

dat_2 <- data.frame(x, p2 = h(-4 + 12 * a_1 - 12 * a_2))
ggplot(dat_2, aes(x=x, y=p2)) + geom_line()+
geom_line(data=dat_p, aes(x=x,y=p), col='red') +ylim(c(0,1))+
   geom_point(data = datos, aes(x = x_1, y = g_1))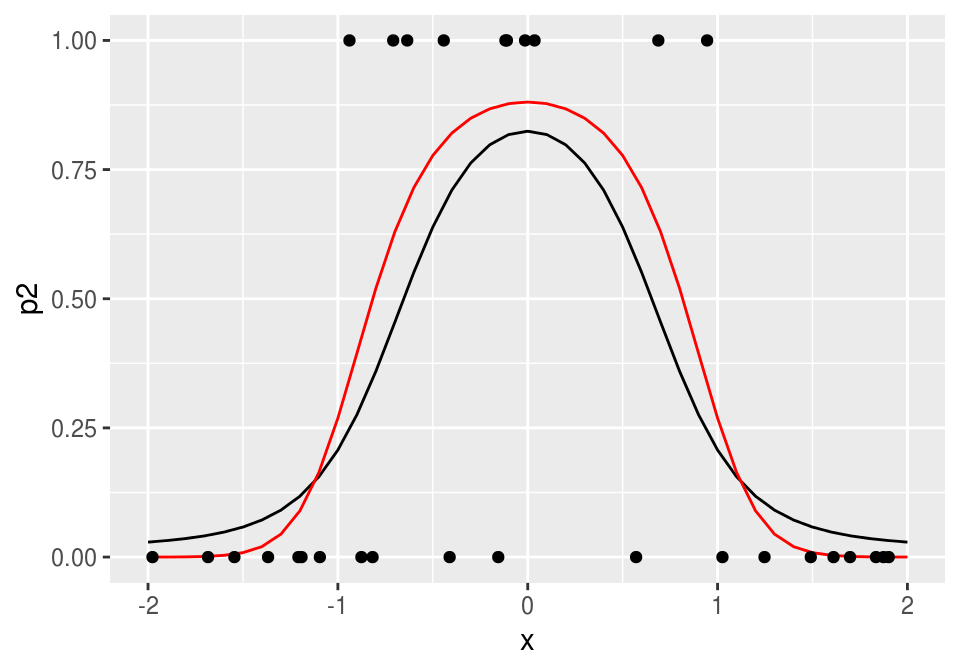

que da un ajuste razonable. Este es un ejemplo de cómo la mezcla de dos funciones logísticas puede replicar esta función con forma de chipote.

¿Cómo ajustar los parámetros?

Para encontrar los mejores parámetros, minimizamos la devianza sobre los parámetros $\beta_0,\beta_1,\beta_{1,0},\beta_{1,1}, \beta_{2,0},\beta_{2,1}$.

Veremos más adelante que conviene hacer esto usando descenso o en gradiente o descenso en gradiente estocástico, pero por el momento usamos la función optim de R para minimizar la devianza. En primer lugar, creamos una función que para todas las entradas calcula los valores de salida. En esta función hacemos feed-forward de las entradas a través de la red para calcular la salida.

## esta función calcula los valores de cada nodo en toda la red,
## para cada entrada
feed_fow <- function(beta, x){
  a_1 <- h(beta[1] + beta[2] * x) # calcula variable 1 de capa oculta
  a_2 <- h(beta[3] + beta[4] * x) # calcula variable 2 de capa oculta
  p <- h(beta[5] + beta[6] * a_1 + beta[7] * a_2) # calcula capa de salida
  p
}

Nótese que simplemente seguimos el diagrama mostrado arriba para hacer los cálculos, combinando linealmente las entradas en cada capa.

Ahora definimos una función para calcular la devianza. Conviene crear una función que crea funciones, para obtener una función que sólo se evalúa en los parámetros para cada conjunto de datos de entrenamiento fijos:

devianza_fun <- function(x, y){
    # esta función es una fábrica de funciones
   devianza <- function(beta){
         p <- feed_fow(beta, x)
      - 2 * mean(y*log(p) + (1-y)*log(1-p))
   }
  devianza
}

Por ejemplo:

dev <- devianza_fun(x_1, g_1) # crea función dev
## ahora dev toma solamente los 7 parámetros beta:
dev(c(0,0,0,0,0,0,0))

## [1] 1.386294

Finalmente, optimizamos la devianza. Para esto usaremos la función optim de R:

set.seed(5)
salida <- optim(rnorm(7), dev, method = 'BFGS') # inicializar al azar punto inicial
salida

## $par
## [1] -24.8192568  23.0201169  -8.4364869  -6.7633494   0.9849461 -14.0157655
## [7] -14.3394673
## 
## $value
## [1] 0.654347
## 
## $counts
## function gradient 
##      103      100 
## 
## $convergence
## [1] 1
## 
## $message
## NULL

beta <- salida$par

Y ahora podemos graficar con el vector $\beta$ encontrado:

## hacer feed forward con beta encontrados
p_2 <- feed_fow(beta, x)
dat_2 <- data.frame(x, p_2 = p_2)
ggplot(dat_2, aes(x = x, y = p_2)) + geom_line()+
geom_line(data = dat_p, aes(x = x, y = p), col='red') +ylim(c(0,1))+
   geom_point(data = datos, aes(x = x_1, y = g_1))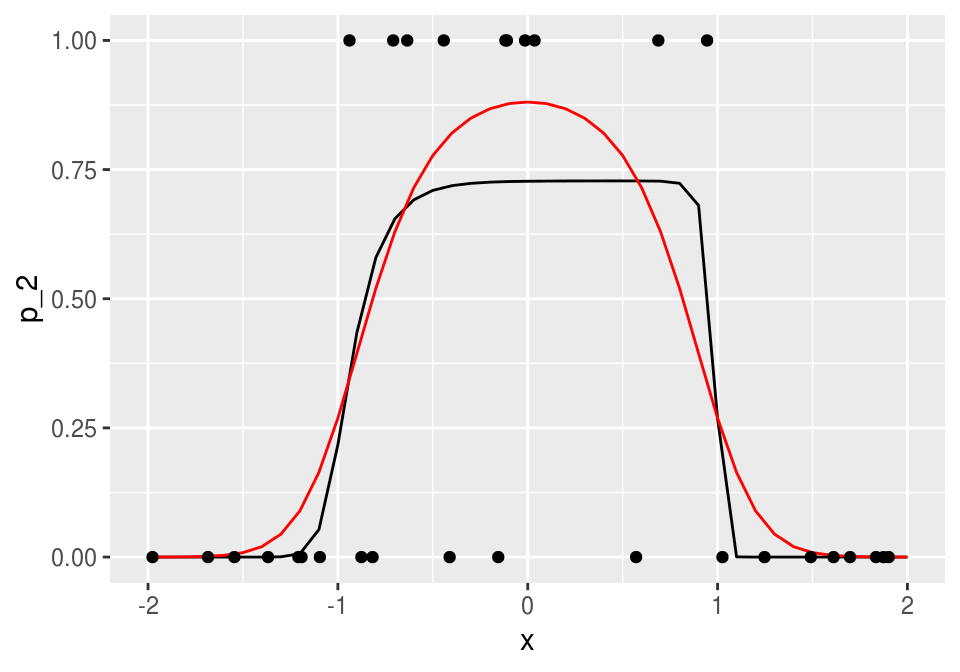

Los coeficientes estimados, que en este caso muchas veces se llaman pesos, son:

beta

## [1] -24.8192568  23.0201169  -8.4364869  -6.7633494   0.9849461 -14.0157655
## [7] -14.3394673

que parecen ser muy grandes. Igualmente, de la figura vemos que el ajuste no parece ser muy estable (esto se puede confirmar corriendo con distintos conjuntos de entrenamiento). Podemos entonces regularizar ligeramente la devianza para resolver este problema. En primer lugar, definimos la devianza regularizada (ridge), donde penalizamos todos los coeficientes que multiplican a una variable, pero no los intercepts:

devianza_reg <- function(x, y, lambda){
    # esta función es una fábrica de funciones
   devianza <- function(beta){
         p <- feed_fow(beta, x)
         # en esta regularizacion quitamos sesgos, pero puede hacerse también con sesgos.
        - 2 * mean(y*log(p) + (1-y)*log(1-p)) + lambda*sum(beta[-c(1,3,5)]^2) 
   }
  devianza
}

dev_r <- devianza_reg(x_1, g_1, 0.001) # crea función dev
set.seed(5)
salida <- optim(rnorm(7), dev_r, method='BFGS') # inicializar al azar punto inicial
salida

## $par
## [1] -4.826652  4.107146 -4.845864 -4.561488  1.067216 -5.236453 -5.195981
## 
## $value
## [1] 0.8322745
## 
## $counts
## function gradient 
##      102      100 
## 
## $convergence
## [1] 1
## 
## $message
## NULL

beta <- salida$par
dev(beta)

## [1] 0.74018

p_2 <- feed_fow(beta, x)
dat_2 <- data.frame(x, p_2 = p_2)
ggplot(dat_2, aes(x = x, y = p_2)) + geom_line()+
geom_line(data = dat_p, aes(x = x, y = p), col='red') +ylim(c(0,1))+
   geom_point(data = datos, aes(x = x_1, y = g_1))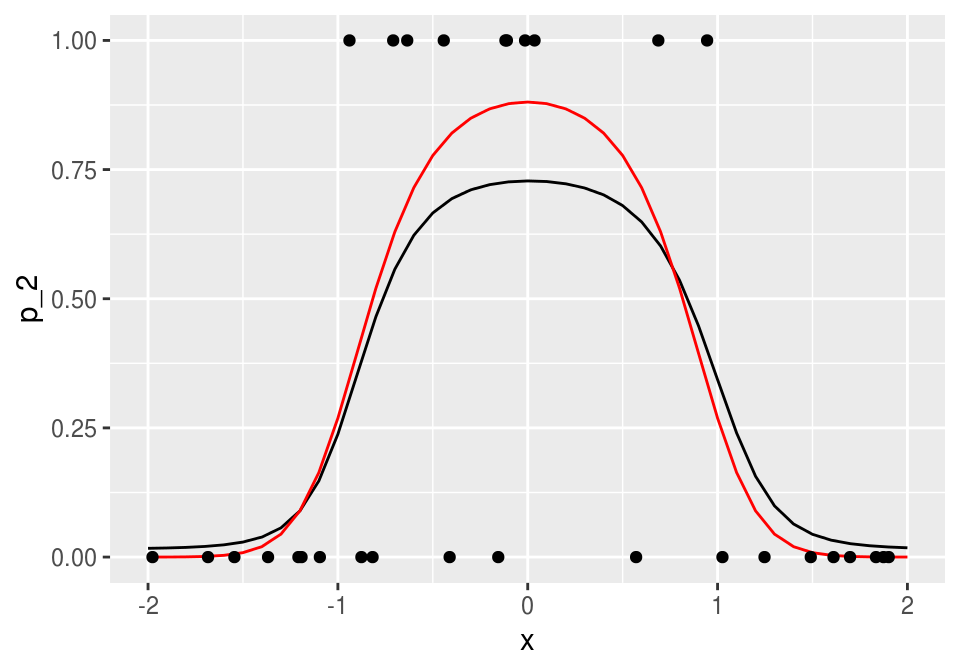

y obtenemos un ajuste mucho más estable. Podemos también usar la función nnet del paquete nnet. Ojo: en nnet, el error es la devianza no está normalizada por número de casos y dividida entre dos:

library(nnet)
set.seed(12)
nn <- nnet(g_1 ~ x_1, data = datos, size = 2, decay = 0.0, entropy = T)

## # weights:  7
## initial  value 19.318858 
## iter  10 value 11.967705
## iter  20 value 10.251964
## iter  30 value 9.647707
## iter  40 value 9.573030
## iter  50 value 9.569389
## iter  60 value 9.555125
## iter  70 value 9.546210
## iter  80 value 9.544512
## iter  90 value 9.539825
## iter 100 value 9.535977
## final  value 9.535977 
## stopped after 100 iterations

nn$wts

## [1] -51.274012  48.789640   8.764849   6.219901 -29.155181 -24.998108
## [7]  30.125349

nn$value

## [1] 9.535977

2*nn$value/30

## [1] 0.6357318

dev(nn$wts)

## [1] 0.6357318

qplot(x, predict(nn, newdata=data.frame(x_1 = x)), geom='line')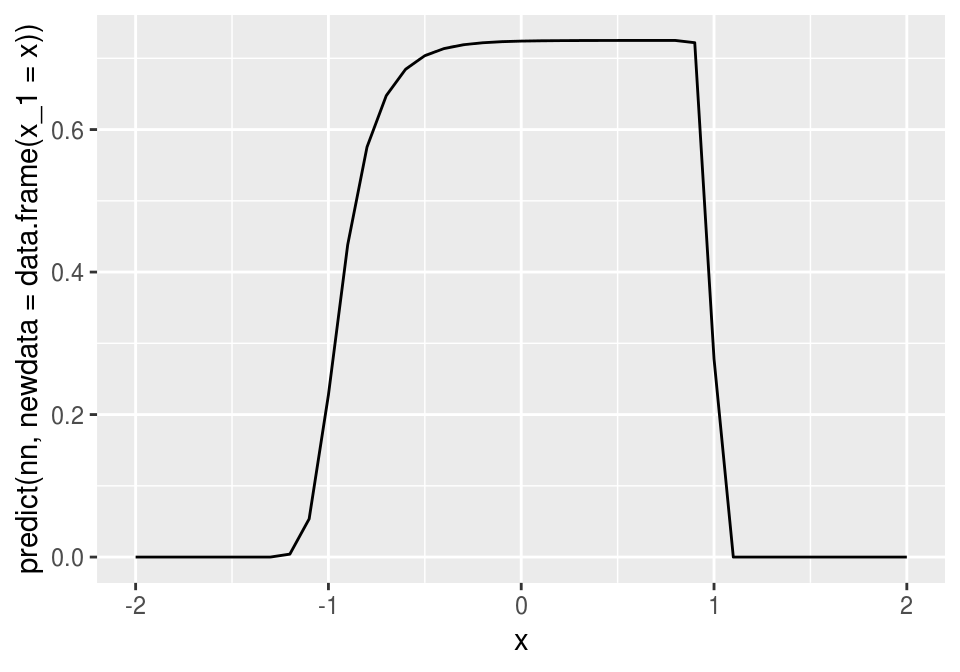

7.1.0.1 Ejercicio

Un ejemplo más complejo. Utiliza los siguientes datos, y agrega si es necesario variables derivadas $a_3, a_4$ en la capa oculta.

h <- function(x){
    exp(x)/(1 + exp(x))
}
x <- seq(-2,2,0.05)
p <- h(3 + x- 3 * x ^ 2 + 3 * cos(4 * x))
set.seed(280572)
x.2 <- runif(300, -2, 2)
g.2 <- rbinom(300, 1, h(3 + x.2 - 3 * x.2 ^ 2 + 3 * cos(4 * x.2)))
datos <- data.frame(x.2,g.2)
dat.p <- data.frame(x,p)
g <- qplot(x,p, geom='line', col='red')
g + geom_jitter(data = datos, aes(x=x.2,y=g.2), col ='black',
  position =position_jitter(height=0.05), alpha=0.4)

7.2 Interacciones en redes neuronales

Es posible capturar interacciones con redes neuronales. Consideremos el siguiente ejemplo simple:

p <- function(x1, x2){
  h(-5 + 10*x1 + 10*x2 - 30*x1*x2)
}
dat <- expand.grid(x1 = seq(0, 1, 0.05), x2 = seq(0, 1, 0.05))
dat <- dat %>% mutate(p = p(x1, x2))
ggplot(dat, aes(x=x1, y=x2)) + geom_tile(aes(fill=p))

Esta función puede entenderse como un o exclusivo: la probabilidad es alta sólo cuando $x_1$ y $x_2$ tienen valores opuestos ($x_1$ grande pero $x_2$ chica y viceversa).

No es posible modelar esta función mediante el modelo logístico (sin interacciones). Pero podemos incluir la interacción en el modelo logístico o intentar usar una red neuronal. Primero simulamos unos datos y probamos el modelo logístico con y sin interacciones:

set.seed(322)
n <- 500
dat_ent <- data_frame(x1=runif(n,0,1), x2 = runif(n, 0, 1)) %>%
  mutate(p = p(x1, x2)) %>%
  mutate(y = rbinom(n, 1, p))
mod_1 <- glm(y ~ x1 + x2, data = dat_ent, family = 'binomial')
mod_1

## 
## Call:  glm(formula = y ~ x1 + x2, family = "binomial", data = dat_ent)
## 
## Coefficients:
## (Intercept)           x1           x2  
##    -0.01011     -1.47942     -1.19196  
## 
## Degrees of Freedom: 499 Total (i.e. Null);  497 Residual
## Null Deviance:       529.4 
## Residual Deviance: 504.5     AIC: 510.5

table(predict(mod_1) > 0.5, dat_ent$y)

##        
##           0   1
##   FALSE 389 111

mod_2 <- glm(y ~ x1 + x2 + x1:x2, data = dat_ent, family = 'binomial')
mod_2

## 
## Call:  glm(formula = y ~ x1 + x2 + x1:x2, family = "binomial", data = dat_ent)
## 
## Coefficients:
## (Intercept)           x1           x2        x1:x2  
##      -4.726        9.641        9.831      -32.466  
## 
## Degrees of Freedom: 499 Total (i.e. Null);  496 Residual
## Null Deviance:       529.4 
## Residual Deviance: 305.6     AIC: 313.6

table(predict(mod_2) > 0.5, dat_ent$y)

##        
##           0   1
##   FALSE 374  60
##   TRUE   15  51

Observese la gran diferencia de devianza entre los dos modelos (en este caso, el sobreajuste no es un problema).

Ahora consideramos qué red neuronal puede ser apropiada.

set.seed(11)
nn <- nnet(y ~ x1 + x2, data = dat_ent, size = 3, decay = 0.001, 
           entropy = T, maxit = 500)

## # weights:  13
## initial  value 294.186925 
## iter  10 value 233.560013
## iter  20 value 195.096851
## iter  30 value 190.466423
## iter  40 value 184.454612
## iter  50 value 170.767082
## iter  60 value 156.347417
## iter  70 value 153.521658
## iter  80 value 153.069566
## iter  90 value 152.852374
## iter 100 value 152.835812
## iter 110 value 152.826924
## iter 120 value 152.825819
## final  value 152.825815 
## converged

#primera capa
matrix(round(nn$wts[1:9], 1), 3,3, byrow=T)

##      [,1] [,2] [,3]
## [1,] -2.2  3.0 -2.4
## [2,] -8.2  5.9  8.7
## [3,] -2.7 -1.6  3.6

#segunda capa
round(nn$wts[10:13], 1)

## [1] -5.7 15.1 -8.6 19.8

#2*nn$value

El cálculo de esta red es:

feed_fow <- function(beta, x){
  a_1 <- h(beta[1] + beta[2]*x[1] + beta[3]*x[2]) 
  a_2 <- h(beta[4] + beta[5]*x[1] + beta[6]*x[2]) 
  a_3 <- h(beta[7] + beta[8]*x[1] + beta[9]*x[2])
  p <- h(beta[10]+beta[11]*a_1 + beta[12]*a_2 + beta[13]*a_3) # calcula capa de salida
  p
}

Y vemos que esta red captura la interacción:

feed_fow(nn$wts, c(0,0))

## [1] 0.04946031

feed_fow(nn$wts, c(0,1))

## [1] 0.9560235

feed_fow(nn$wts, c(1,0))

## [1] 0.9830594

feed_fow(nn$wts, c(1,1))

## [1] 0.004197137

dat <- dat %>% rowwise %>% mutate(p_red = feed_fow(nn$wts, c(x1, x2)))
ggplot(dat, aes(x=x1, y=x2)) + geom_tile(aes(fill=p_red))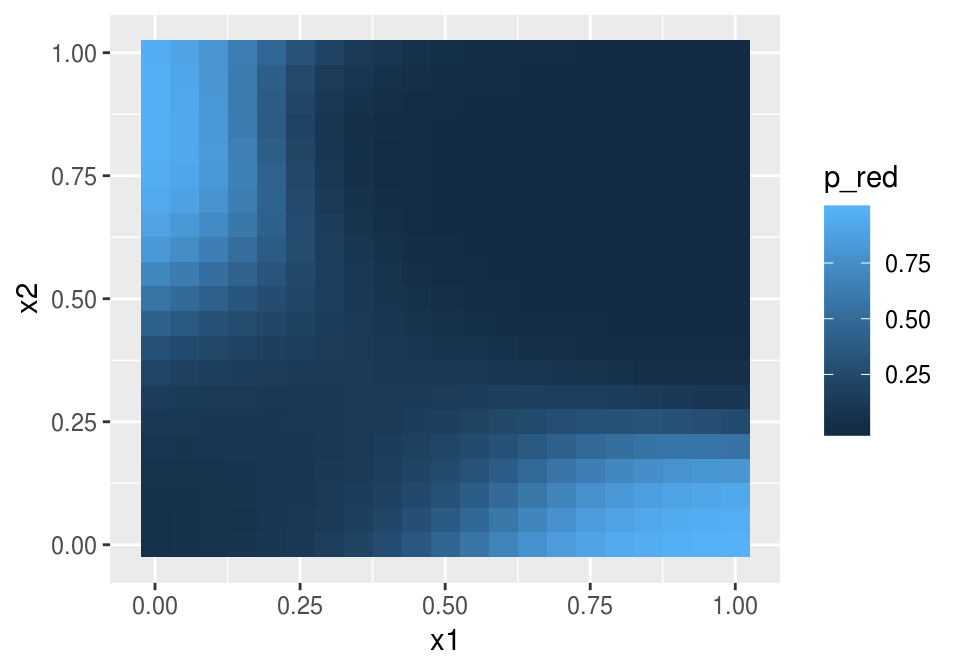

Observación: ¿cómo funciona esta red? Consideremos la capa intermedia.

dat_entrada <- data_frame(x_1 = c(0,0,1,1), x_2 = c(0,1,0,1))
a_1 <- dat_entrada %>% rowwise() %>% mutate(a_1 = h(sum(nn$wts[1:3] * c(1,x_1,x_2) )))
a_2 <- dat_entrada %>% rowwise() %>% mutate(a_2 = h(sum(nn$wts[4:6] * c(1,x_1,x_2) )))
a_3 <- dat_entrada %>% rowwise() %>% mutate(a_3 = h(sum(nn$wts[7:9] * c(1,x_1,x_2) )))
capa_intermedia <- left_join(a_1, a_2) %>% left_join(a_3)

## Joining, by = c("x_1", "x_2")
## Joining, by = c("x_1", "x_2")

a_1

## Source: local data frame [4 x 3]
## Groups: <by row>
## 
## # A tibble: 4 x 3
##     x_1   x_2    a_1
##   <dbl> <dbl>  <dbl>
## 1     0     0 0.102 
## 2     0     1 0.0101
## 3     1     0 0.686 
## 4     1     1 0.164

a_3

## Source: local data frame [4 x 3]
## Groups: <by row>
## 
## # A tibble: 4 x 3
##     x_1   x_2    a_3
##   <dbl> <dbl>  <dbl>
## 1     0     0 0.0629
## 2     0     1 0.709 
## 3     1     0 0.0130
## 4     1     1 0.324

a_2

## Source: local data frame [4 x 3]
## Groups: <by row>
## 
## # A tibble: 4 x 3
##     x_1   x_2      a_2
##   <dbl> <dbl>    <dbl>
## 1     0     0 0.000284
## 2     0     1 0.621   
## 3     1     0 0.0960  
## 4     1     1 0.998

Y observamos que las unidades $a_1$ y $a_3$ tienen valor alto cuando las variables $x_1$ y $x_2$, correspondientemente, tienen valores altos. La unidad $a_2$ responde cuando tanto como $x_1$y $x_2$ tienen valores altos.

En la capa final, le damos peso relativamente alto a las unidades $a_1$ y $a_3$, y peso negativo a la unidad $a_2$

nn$wts[10:13]

## [1] -5.747250 15.138708 -8.628917 19.801144

capa_final <- capa_intermedia %>% rowwise() %>% 
  mutate(p= h(sum(nn$wts[10:13]*c(1,a_1,a_2,a_3) ))) %>%
  mutate(p=round(p,2))
capa_final

## Source: local data frame [4 x 6]
## Groups: <by row>
## 
## # A tibble: 4 x 6
##     x_1   x_2    a_1      a_2    a_3     p
##   <dbl> <dbl>  <dbl>    <dbl>  <dbl> <dbl>
## 1     0     0 0.102  0.000284 0.0629  0.05
## 2     0     1 0.0101 0.621    0.709   0.96
## 3     1     0 0.686  0.0960   0.0130  0.98
## 4     1     1 0.164  0.998    0.324   0

7.3 Cálculo en redes: feed-forward

Ahora generalizamos lo que vimos arriba para definir la arquitectura básica de redes neuronales y cómo se hacen cálculos en las redes.

A las variables originales les llamamos capa de entrada de la red, y a la variable de salida capa de salida. Puede haber más de una capa intermedia. A estas les llamamos capas ocultas.

Cuando todas las conexiones posibles de cada capa a la siguiente están presente, decimos que la red es completamente conexa.

Como vimos en el ejemplo de arriba, para hacer cálculos en la red empezamos con la primera capa, hacemos combinaciones lineales y aplicamos nuestra función no lineal $h$. Una vez que calculamos la segunda capa, podemos calcular la siguiente de la misma forma: combinaciones lineales y aplicación de $h$. Y así sucesivamente hasta que llegamos a la capa final.

Notación

Sea $L$ el número total de capas. En primer lugar, para un cierto caso de entrada $x = (x_1,x_2,\ldots, x_p)$, denotamos por:

$a^{(l)}_j$ el valor que toma la unidad $j$ de la capa $l$, para $j=0,1,\ldots, n_{l}$, donde $n_l$ es el número de unidades de la capa $l$.
Ponemos $a^{(l)}_0=1$ para lidiar con los sesgos.
En particular, ponemos $a^{(1)}_j = x_j$, que son los valores de las entradas (primera capa)
Para clasificación binaria, la última capa solo tiene un elemento, que es $p_1 = a^{(L)}$. Para un problema de clasificación en $K>2$ clases, tenemos que la última capa es de tamaño $K$: $p_1 = a^{(L)}_1, p_2 = a^{(L)}_2,\ldots, p_K = a^{(L)}_K$

Adicionalmente, escribimos

$\theta_{i,k}^{(l)}=$ es el peso de entrada $a_{k}^{(l-1)}$ de capa $l-1$ en la entrada $a_{i}^{(l)}$ de la capa $l$.

Los sesgos están dados por \[\theta_{i,0}^{(l)}\]

Ejemplo

En nuestro ejemplo, tenemos que en la capa $l=3$ hay dos unidades. Así que podemos calcular los valores $a^{(3)}_1$ y $a^{(3)}_2$. Están dados por

\[a_1^{(3)} = h(\theta_{1,0}^{(2)} + \theta_{1,1}^{(2)} a_1^{(2)}+ \theta_{1,2}^{(2)}a_2^{(2)}+ \theta_{1,3}^{(2)} a_3^{(2)})\] \[a_2^{(3)} = h(\theta_{2,0}^{(2)} + \theta_{2,1}^{(2)} a_1^{(2)}+ \theta_{2,2}^{(2)}a_2^{(2)}+ \theta_{2,3}^{(2)} a_3^{(2)})\]

Como se ilustra en la siguiente gráfica:

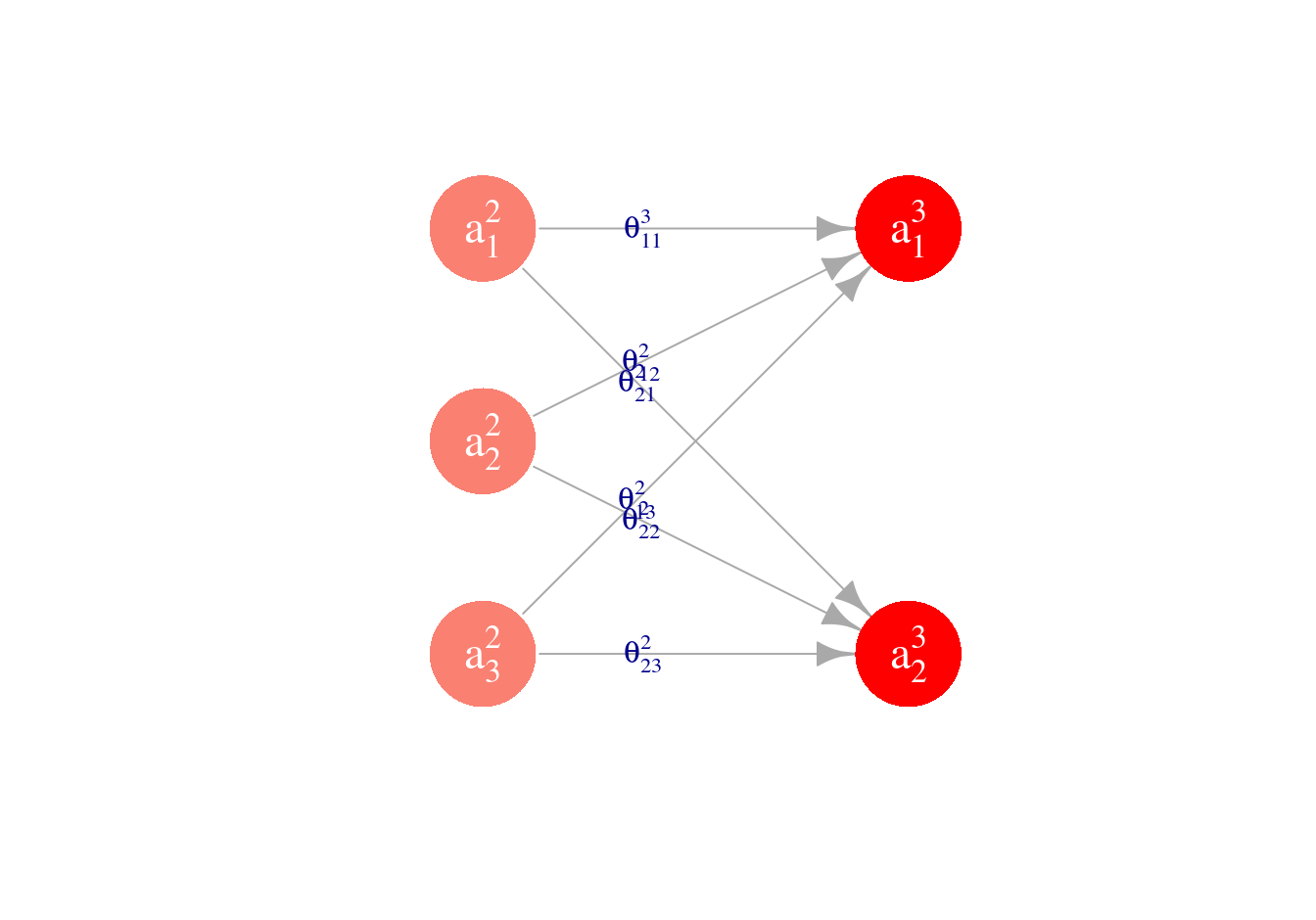
Para visualizar las ordenadas (que también se llaman sesgos en este contexto), ponemos $a_{0}^{(2)}=1$.

Ejemplo

Consideremos propagar a la capa 3 a partir de la capa 2. Usaremos los siguientes pesos para capa 3 y valores de la capa 2 (en gris están los sesgos):

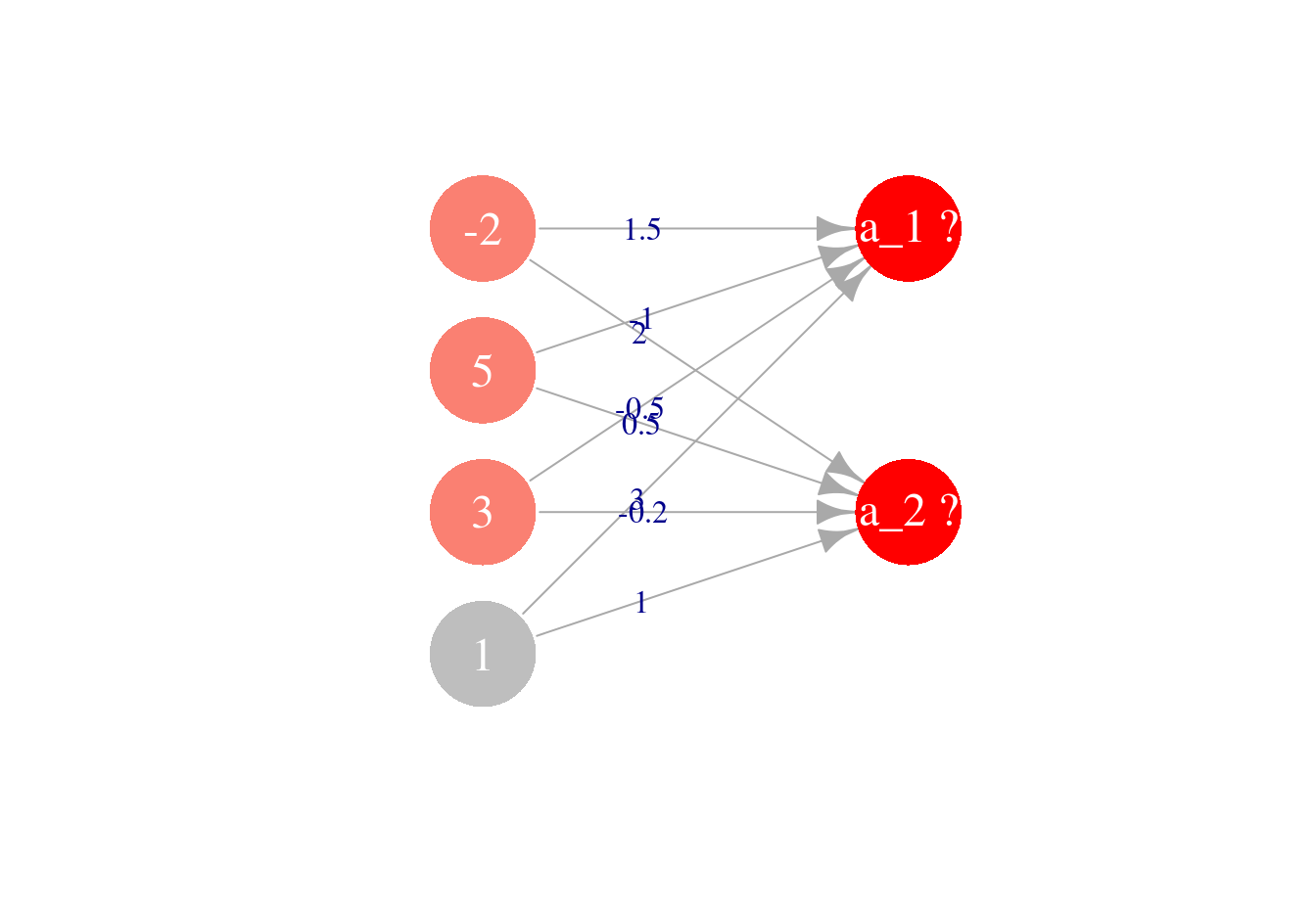
Que en nuestra notación escribimos como \[a^{(2)}_0 = 1, a^{(2)}_1 = -2, a^{(2)}_2 = 5, a^{(2)}=3\] y los pesos son, para la primera unidad: \[\theta^{(2)}_{1,0} = 3, \,\,\, \theta^{(2)}_{1,1} = 1.5,\,\,\,\theta^{(2)}_{1,2} = -1,\,\,\theta^{(2)}_{1,3} = -0.5 \] y para la segunda unidad \[\theta^{(2)}_{2,0} = 1, \,\,\, \theta^{(2)}_{2,1} = 2,\,\,\,\theta^{(2)}_{2,2} = 0.5,\,\, \theta^{(2)}_{2,3} = -0.2\] Y ahora queremos calcular los valores que toman las unidades de la capa 3, que son $a^{(3)}_1$ y $a^{(3)}_2$$

Para hacer feed forward a la siguiente capa, hacemos entonces

\[a^{(3)}_1 = h(3 + a^{(2)}_1 - a^{(2)}_2 -0.5 a_3^{(2)}),\] \[a^{(3)}_2 = h(1 + 2a^{(2)}_1 + 0.5a^{(2)}_2 - 0.2 a_3^{(2)}),\]

Ponemos los pesos y valores de la capa 2 (incluyendo sesgo):

a_2 <- c(1, -2, 5, 3) # ponemos un 1 al principio para el sesgo
theta_2_1 = c(3, 1.5, -1.0, -0.5)
theta_2_2 = c(1, 2, 0.5, -0.2)

y calculamos

a_3 <- c(1, h(sum(theta_2_1*a_2)),h(sum(theta_2_2*a_2))) # ponemos un 1 al principio
a_3

## [1] 1.000000000 0.001501182 0.249739894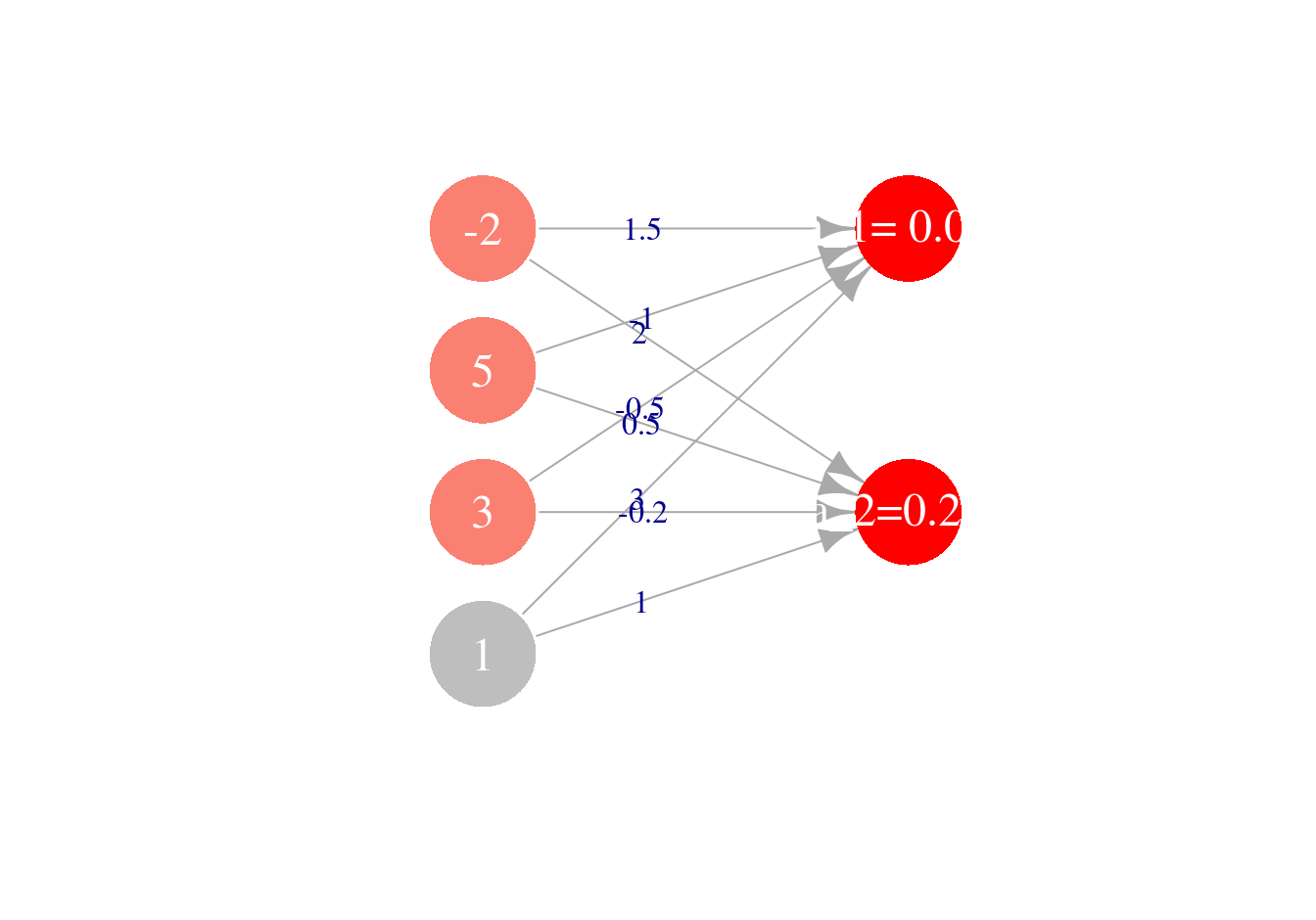

7.4 Feed forward

Para calcular los valores de salida de una red a partir de pesos y datos de entrada, usamos el algoritmo feed-forward, calculando capa por capa.

Cálculo en redes: Feed-forward

Para la primera capa, escribimos las variables de entrada: \[a^{(1)}_j = x_j, j=1\ldots,n_1\] Para la primera capa oculta, o la segunda capa \[a^{(2)}_j = h\left( \theta_{j,0}^{(1)}+ \sum_{k=1}^{n_1} \theta_{j,k}^{(1)} a^{(1)}_k \right), j=1\ldots,n_2\] para la $l$-ésima capa: \[a^{(l)}_j = h\left( \theta_{j,0}^{(l-1)}+ \sum_{k=1}^{n_{l-1}} \theta_{j,k}^{(l-1)} a^{(l-1)}_k \right), j=1\ldots,n_{l}\] y así sucesivamente. Para la capa final o capa de salida (para problema binario), suponiendo que tenemos $L$ capas ($L-2$ capas ocultas): \[p_1 = h\left( \theta_{1,0}^{(L-1)}+ \sum_{k=1}^{n_{L-1}} \theta_{1,k}^{(L-1)} a^{(L-1)}_k \right).\]

Nótese que entonces:

Cada capa se caracteriza por el conjunto de parámetros $\Theta^{(l)}$, que es una matriz de $n_l\times n_{l-1}$.

La red completa entonces se caracteriza por:

La estructura elegida (número de capas ocultas y número de nodos en cada capa oculta).
Las matrices de pesos en cada capa $\Theta^{(1)},\Theta^{(2)},\ldots, \Theta^{(L-1)}$

Adicionalmente, escribimos en forma vectorial: \[a^{(l)} = (a^{(l)}_0, a^{(l)}_1, a^{(l)}_2, \ldots, a^{(l)}_{n_l})^t\]

Para calcular la salidas, igual que hicimos, antes, propagaremos hacia adelante los valores de las variables de entrada usando los pesos. Agregando entradas adicionales en cada capa $a_0^{(l)}$, $l=1,2,\ldots, L-1$, donde $a_0^{l}=1$, y agregando a $\Theta^{(l)}$ una columna con las ordenadas al origen (o sesgos) podemos escribir:

Feed-forward(matricial)

Capa 1 (vector de entradas) \[ a^{(1)} = x\]
Capa 2 \[ a^{(2)} = h(\Theta^{(1)}a^{(1)})\]
Capa $l$ (oculta) \[ a^{(l)} = h(\Theta^{(l-1)}a^{(l-1)})\]
Capa de salida:

En un problema de clasificación binaria, la capa de salida se calcula como en regresión logística: \[a^{(L)}= p = h(\Theta^{(L-1)}a^{(L-1)})\] donde $h$ se aplica componente a componente sobre los vectores correspondientes. Nótese que feed-foward consiste principalmente de multiplicaciones de matrices con algunas aplicaciones de $h$

Para un problema de regresión, la última capa se calcula como en regresión lineal:

\[a^{(L)} = p = \Theta^{(L-1)}a^{(L-1)}\]

7.5 Backpropagation: cálculo del gradiente (clasificación binaria)

Más adelante, para ajustar los pesos y sesgos de las redes (valores $\theta$), utilizaremos descenso en gradiente y otros algoritmos derivados del gradiente (descenso estocástico). En esta parte entonces veremos cómo calcular estos gradientes con el algoritmo de back-propagation, que es una aplicación de la regla de la cadena para derivar. Back-propagation resulta en una fórmula recursiva donde propagamos errores de la red como gradientes desde el final de red (capa de salida) hasta el principio, capa por capa.

Consideramos el problema de clasificación binaria

Recordamos la devianza (con regularización ridge) es

\[D = -\frac{2}{n}\sum_{i=1}^n y_i\log(p_1(x_i)) +(1-y_i)\log(1-p_1(x_i)) + \lambda \sum_{l=2}^{L} \sum_{k=1}^{n_{l-1}} \sum_{j=1}^{n_l}(\theta_{j,k}^{(l)})^2.\]

Queremos entonces calcular las derivadas de la devianza con respecto a cada parámetro $\theta_{j,k}^{(l)}$. Esto nos proporciona el gradiente para nuestro algoritmo de descenso.

Consideramos aquí el problema de clasificación binaria con devianza como función de pérdida, y sin regularización. La parte de la parcial que corresponde al término de regularización es fácil de agregar al final.

Recordamos también nuestra notación para la función logística (o sigmoide):

\[h(z)=\frac{1}{1+e^{-z}}.\] Necesitaremos su derivada, que está dada por (cálculala): \[h'(z) = h(z)(1-h(z))\]

7.5.1 Cálculo para un caso de entrenamiento

Como hicimos en regresión logística, primero simplificamos el problema y consideramos calcular las parciales para un solo caso de entrenamiento $(x,y)$: \[ D= -\left ( y\log (p_1(x)) + (1-y)\log (1-p_1(x))\right) . \]

Después sumaremos sobre toda la muestra de entrenamiento. Entonces queremos calcular \[\frac{\partial D}{\partial \theta_{j,k}^{(l)}}\]

Y escribiremos, con la notación de arriba, \[a^{(l+1)}_j = h(z^{(l+1)}_j)\] donde \[z^{(l+1)} = \Theta^{(l)} a^{(l)},\] que coordenada a coordenada se escribe como \[z^{(l+1)}_j = \sum_{k=0}^{n_{l}} \theta_{j,k}^{(l)} a^{(l)}_k\]

Paso 1: Derivar respecto a capa $l+1$

Como los valores de cada capa determinan los valores de salida y la devianza, podemos escribir (recordemos que $a_0^{(l)}=1$ es constante): \[D=D(a_0^{(l+1)},a_1^{(l+1)},a_2^{(l+1)},\ldots, a_{n_{l+1}}^{(l+1)})=D(a_1^{(l+1)},a_2^{(l+1)},\ldots, a_{n_{l+1}}^{(l+1)})\]

Así que por la regla de la cadena para varias variables: \[\frac{\partial D}{\partial \theta_{j,k}^{(l)}} = \sum_{t=1}^{n_{l}} \frac{\partial D}{\partial a_t^{(l+1)}}\frac{\partial a_t^{(l+1)}} {\partial \theta_{j,k}^{(l)} }\]

Pero si vemos dónde aparece $\theta_{j,k}^{(l)}$ en la gráfica de la red:

\[ \cdots a^{(l)}_k \xrightarrow{\theta_{j,k}^{(l)}} a^{(l+1)}_j \cdots \rightarrow D\] Entonces podemos concluir que $\frac{\partial a_t^{(l+1)}}{\partial \theta_{j,k}^{(l)}} =0$ cuando $t\neq j$ (pues no dependen de $\theta_{j,k}^{(l)}$),

y entonces, para toda $j=1,2,\ldots, n_{l+1}, k=0,1,\ldots, n_{l}$ \[\begin{equation} \frac{\partial D}{\partial \theta_{j,k}^{(l)}} = \frac{\partial D}{\partial a_j^{(l+1)}}\frac{\partial a_j^{(l+1)}}{\partial \theta_{j,k}^{(l)} } . \tag{7.1} \end{equation}\]

Adicionalmente, como \[a_j^{(l+1)} = h(z_j^{(l+1)}) = h\left (\sum_{k=0}^{n_{l}} \theta_{j,k}^{(l)} a^{(l)}_k \right )\] y las $a_k^{(l)}$ no dependen de $\theta_{j,k}^{(l)}$, tenemos por la regla de la cadena que \[\begin{equation} \frac{\partial a_j^{(l+1)}}{\partial \theta_{j,k}^{(l)} } = h'(z_j^{(l+1)})a_k^{(l)}. \end{equation}\]

Esta última expresión podemos calcularla pues sólo requiere la derivada de $h$ y los valores otenidos en el paso de feed-forward.

Paso 2: Obtener fórmula recursiva

Así que sólo nos queda calcular las parciales ($j = 1,\ldots, n_l$) \[\frac{\partial D}{\partial a_j^{(l)}}\]

Para obtener una fórmula recursiva para esta cantidad (hacia atrás), aplicamos otra vez regla de la cadena, pero con respecto a la capa $l$ (ojo: queremos obtener una fórmula recursiva!):

\[\frac{\partial D}{\partial a_j^{(l)}}= \sum_{s=1}^{n_{l+1}} \frac{\partial D}{\partial a_s^{(l+1)}}\frac{\partial a_s^{(l+1)}}{\partial a_j^{(l)}},\]

que se puede entender a partir de este diagrama:

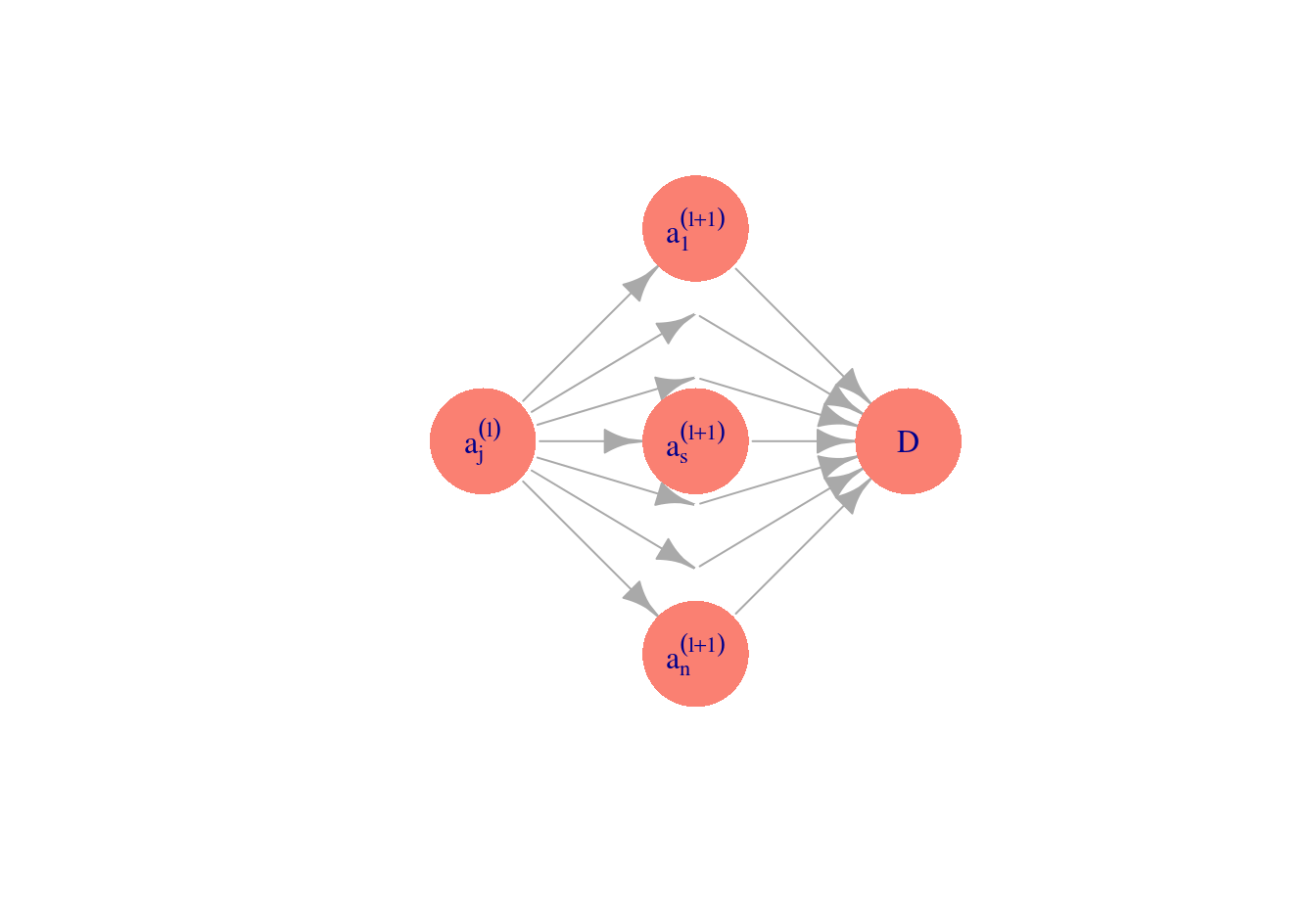
Nótese que la suma empieza en $s=1$, no en $s=0$, pues $a_0^{(l+1)}$ no depende de $a_k^{(l)}$.

En este caso los elementos de la suma no se anulan necesariamente. Primero consideramos la derivada de:

\[\frac{\partial a_s^{(l+1)}}{\partial a_j^{(l)}}=h'(z_s^{(l+1)})\theta_{s,j}^{(l)},\]

de modo que

\[\frac{\partial D}{\partial a_j^{(l)}}= \sum_{s=1}^{n_l} \frac{\partial D}{\partial a_s^{(l+1)}} h'(z_s^{(l+1)})\theta_{s,j}^{(l)}.\]

Nótese que esto nos da una fórmula recursiva para las parciales que nos falta calcular (de $D$ con respecto a $a$), pues las otras cantidades las conocemos por backpropagation.

Paso 3: Simplificación de la recursión

\[\begin{equation} \delta_s^{ (l+1)}=\frac{\partial D}{\partial a_s^{(l+1)}} h'(z_s^{(l+1)}) \tag{7.2} \end{equation}\]

de manera que la ecuación recursiva es

\[\begin{equation} \frac{\partial D}{\partial a_j^{(l)}} = \sum_{s=1}^{n_{l+1}} \delta_s^{(l+1)}\theta_{s,j}^{(l)}. \tag{7.3} \end{equation}\]

Tenemos que si $l=2,\ldots,L-1$, entonces podemos escribir (usando (7.3)) como fórmula recursiva:

\[\begin{equation} \delta_j^{(l)} = \left (\sum_{s=1}^{n_l} \delta_s^{(l+1)} \theta_{s,j}^{(l)}\right ) h'(z_j^{(l)}), \tag{7.4} \end{equation}\] para $j=1,2,\ldots, n_{l}$.

Paso 4: Condiciones inciales

Para la última capa, tenemos que (demostrar!)

\[\delta_1^{(L)}=p - y.\]

Paso 5: Cálculo de parciales

Finalmente, usando (7.1) y (7.2) , obtenemos \[\frac{\partial D}{\partial \theta_{j,k}^{(l)}} = \delta_j^{(l+1)}a_k^{(l)},\]

y con esto ya podemos hacer backpropagation para calcular el gradiente sobre cada caso de entrenamiento, y solo resta acumular para obtener el gradiente sobre la muestra de entrenamiento.

Muchas veces es útil escribir una versión vectorizada (importante para implementar):

Paso 6: Versión matricial

Ahora podemos escribir estas ecuaciones en forma vectorial. En primer lugar, \[\delta^{(L)}=p-y.\] Y además se puede ver de la ecuación (7.4) que ($\Theta_{*}^{(l+1)}$ denota la matriz de pesos sin la columna correspondiente al sesgo):

\[\begin{equation} \delta^{(l)}=\left( \Theta_{*}^{(l)} \right)^t\delta^{(l+1)} \circ h'(z^{(l)}) \tag{7.5} \end{equation}\]

donde $\circ$ denota el producto componente a componente.

Ahora todo ya está calculado. Lo interesante es que las $\delta^{(l)}$ se calculan de manera recursiva.

7.5.2 Algoritmo de backpropagation

Backpropagation Para problema de clasificación con regularización $ 0 $. Para $i=1,\ldots, N,$ tomamos el dato de entrenamiento $(x^{(i)}, y^{(i)})$ y hacemos:

Ponemos $a^{(1)}=x^{(i)}$ (vector de entradas, incluyendo 1).
Calculamos $a^{(2)},a^{(3)},\ldots, a^{(L)}$ usando feed forward para la entrada $x^{(i)}.$
Calculamos $\delta^{(L)}=a^{(L)}-y^{(i)}$, y luego $\delta^{(L-1)},\ldots, \delta^{(2)}$ según la recursión (7.4).
Acumulamos $\Delta_{j,k}^{(l)}=\Delta_{j,k}^{(l)} + \delta_j^{(l+1)}a_k^{(l)}$.
Finalmente, ponemos, si $k\neq 0$, \[D_{j,k}^{(l)} = \frac{2}{N}\Delta_{j,k}^{(l)} + 2\lambda\theta_{j,k}^{(l)}\] y si $k=0$, \[D_{j,k}^{(l)} = \frac{2}{N}\Delta_{j,k}^{(l)} .\] Entonces: \[D_{j,k}^{(l)} =\frac{\partial D}{\partial \theta_{j,k}^{(l)}}.\]

Nótese que back-propagation consiste principalmente de mutliplicaciones de matrices con algunas aplicaciones de $h$ y acumulaciones, igual que feed-forward.

7.6 Ajuste de parámetros (introducción)

Consideramos la versión con regularización ridge (también llamada L2) de la devianza de entrenamiento como nuestro función objetivo:

Ajuste de redes neuronales Para un problema de clasificación binaria con $y_i=0$ o $y_i=1$, ajustamos los pesos $\Theta^{(1)},\Theta^{(2)},\ldots, \Theta^{(L)}$ de la red minimizando la devianza (penalizada) sobre la muestra de entrenamiento: \[D = -\frac{2}{n}\sum_{i=1}^n y_i\log(p_1(x_i)) +(1-y_i)\log(1-p_1(x_i)) + \lambda \sum_{l=2}^{L} \sum_{k=1}^{n_{l-1}} \sum_{j=1}^{n_l}(\theta_{j,k}^{(l)})^2.\] Este problema en general no es convexo y puede tener múltiples mínimos.

Veremos el proceso de ajuste, selección de arquitectura, etc. más adelante. Por el momento hacemos unas observaciones acerca de este problema de minimización:

Hay varios algoritmos para minimizar esta devianza, algunos avanzados incluyendo información de segundo orden (como Newton), pero actualmente las técnicas más populares, para redes grandes, están derivadas de descenso en gradiente. Más específicamente, una variación, que es descenso estocástico.
Que el algoritmo depende principalmente de multiplicaciones de matrices y acumulaciones implica que puede escalarse de diversas maneras. Una es paralelizando sobre la muestra de entrenamiento (y acumular acumulados al final), pero también se puede paralelizar la de multiplicaciones de matrices (para lo cual los GPUs se prestan muy bien).
Para redes neuronales, el gradiente se calcula con un algoritmo que se llama back-propagation, que es una aplicación de la regla de la cadena para propagar errores desde la capa de salida a lo largo de todas las capas para ajustar los pesos y sesgos.
En estos problemas no buscamos el mínimo global, sino un mínimo local de buen desempeño. Puede haber múltiples mínimos, puntos silla, regiones relativamente planas, precipicios (curvatura alta). Todo esto dificulta el entrenamiento de redes neuronales grandes. Para redes grandes, ni siquiera esperamos a alcanzar un mínimo local, sino que nos detenemos prematuramente cuando obtenemos el mejor desempeño posible.
Nótese que la simetría implica que podemos obtener la misma red cambiando pesos entre neuronas y las conexiones correspondientes. Esto implica que necesariamente hay varios mínimos.
Para este problema, no tiene sentido comenzar las iteraciones con todos los pesos igual a cero, pues las unidades de la red son simétricas: no hay nada que distinga una de otra si todos los pesos son iguales. Esto quiere decir que si iteramos, ¡todas las neuronas van a aprender lo mismo!
Es importante no comenzar valores de los pesos grandes, pues las funciones logísticas pueden quedar en regiones planas donde la minimización es lenta, o podemos tener gradientes demasiado grandes y produzcan inestabilidad en el cálculo del gradiente.
Generalmente los pesos se inicializan al azar con variables independientes gaussianas o uniformes centradas en cero, y con varianza chica (por ejemplo $U(-0.5,0.5)$). Una recomendación es usar $U(-1/\sqrt{m}, 1/\sqrt{m})$ donde $m$ es el número de entradas. En general, hay que experimentar con este parámetro.

El proceso para ajustar una red es entonces:

Definir número de capas ocultas, número de neuronas por cada capa, y un valor del parámetro de regularización. Estandarizar las entradas.
Seleccionar parámetros al azar para $\Theta^{(2)},\Theta^{(3)},\ldots, \Theta^{(L)}$. Se toman, por ejemplo, normales con media 0 y varianza chica.
Correr un algoritmo de minimización de la devianza mostrada arriba.
Verificar convergencia del algoritmo a un mínimo local (o el algoritmo no está mejorando).
Predecir usando el modelo ajustado.

Finalmente, podemos probar distintas arquitecturas y valores del parámetros de regularización, para afinar estos parámetros según validación cruzada o una muestra de validación.

7.6.1 Ejemplo

Consideramos una arquitectura de dos capas para el problema de diabetes

library(keras)

## 
## Attaching package: 'keras'

## The following objects are masked from 'package:igraph':
## 
##     %<-%, normalize

Escalamos y preparamos los datos:

diabetes_ent <- MASS::Pima.tr
diabetes_pr <- MASS::Pima.te
x_ent <- diabetes_ent %>% select(-type) %>% as.matrix
x_ent_s <- scale(x_ent)
x_valid <- diabetes_pr %>% select(-type) %>% as.matrix 
x_valid_s <- x_valid %>%
  scale(center = attr(x_ent_s, 'scaled:center'), 
        scale = attr(x_ent_s,  'scaled:scale'))
y_ent <- as.numeric(diabetes_ent$type == 'Yes')
y_valid <- as.numeric(diabetes_pr$type == 'Yes')

Para definir la arquitectura de dos capas con:

10 unidades en cada capa
función de activación sigmoide,
regularización L2 (ridge),
salida logística ($p_1$), escribimos:

set.seed(923)
modelo_tc <- keras_model_sequential() 
# no es necesario asignar a nuevo objeto, modelo_tc es modificado al agregar capas
modelo_tc %>% 
  layer_dense(units = 10, activation = 'sigmoid', 
              kernel_regularizer = regularizer_l2(l = 1e-3), 
              kernel_initializer = initializer_random_uniform(minval = -0.5, maxval = 0.5),
              input_shape=7) %>%
  layer_dense(units = 10, activation = 'sigmoid', 
              kernel_regularizer = regularizer_l2(l = 1e-3), 
              kernel_initializer = initializer_random_uniform(minval = -0.5, maxval = 0.5)) %>%
  layer_dense(units = 1, activation = 'sigmoid',
              kernel_regularizer = regularizer_l2(l = 1e-3),
              kernel_initializer = initializer_random_uniform(minval = -0.5, maxval = 0.5)
)

Ahora difinimos la función de pérdida (devianza es equivalente a entropía cruzada binaria), y pedimos registrar porcentaje de correctos (accuracy) y compilamos en tensorflow:

modelo_tc %>% compile(
  loss = 'binary_crossentropy',
  optimizer = optimizer_sgd(lr = 0.8),
  metrics = c('accuracy','binary_crossentropy'))

Iteramos con descenso en gradiente y monitoreamos el error de validación. Hacemos 100 iteraciones de descenso en gradiente (épocas=100)

iteraciones <- modelo_tc %>% fit(
  x_ent_s, y_ent, 
  #batch size mismo que nrow(x_ent_s) es descenso en grad.
  epochs = 1000, batch_size = nrow(x_ent_s), 
  verbose = 1,
  validation_data = list(x_valid_s, y_valid)
)

score <- modelo_tc %>% evaluate(x_valid_s, y_valid)
score

## $loss
## [1] 0.4744743
## 
## $acc
## [1] 0.7861446
## 
## $binary_crossentropy
## [1] 0.4366375

tab_confusion <- table(modelo_tc %>% predict_classes(x_valid_s),y_valid) 
tab_confusion

##    y_valid
##       0   1
##   0 194  42
##   1  29  67

prop.table(tab_confusion, 2)

##    y_valid
##             0         1
##   0 0.8699552 0.3853211
##   1 0.1300448 0.6146789

Es importante monitorear las curvas de aprendizaje (entrenamiento y validación) para diagnosticar mejoras:

df_iteraciones <- as.data.frame(iteraciones)
ggplot(df_iteraciones, aes(x=epoch, y=value, colour=data, group=data)) + 
  geom_line() + geom_point() + facet_wrap(~metric, ncol=1, scales = 'free')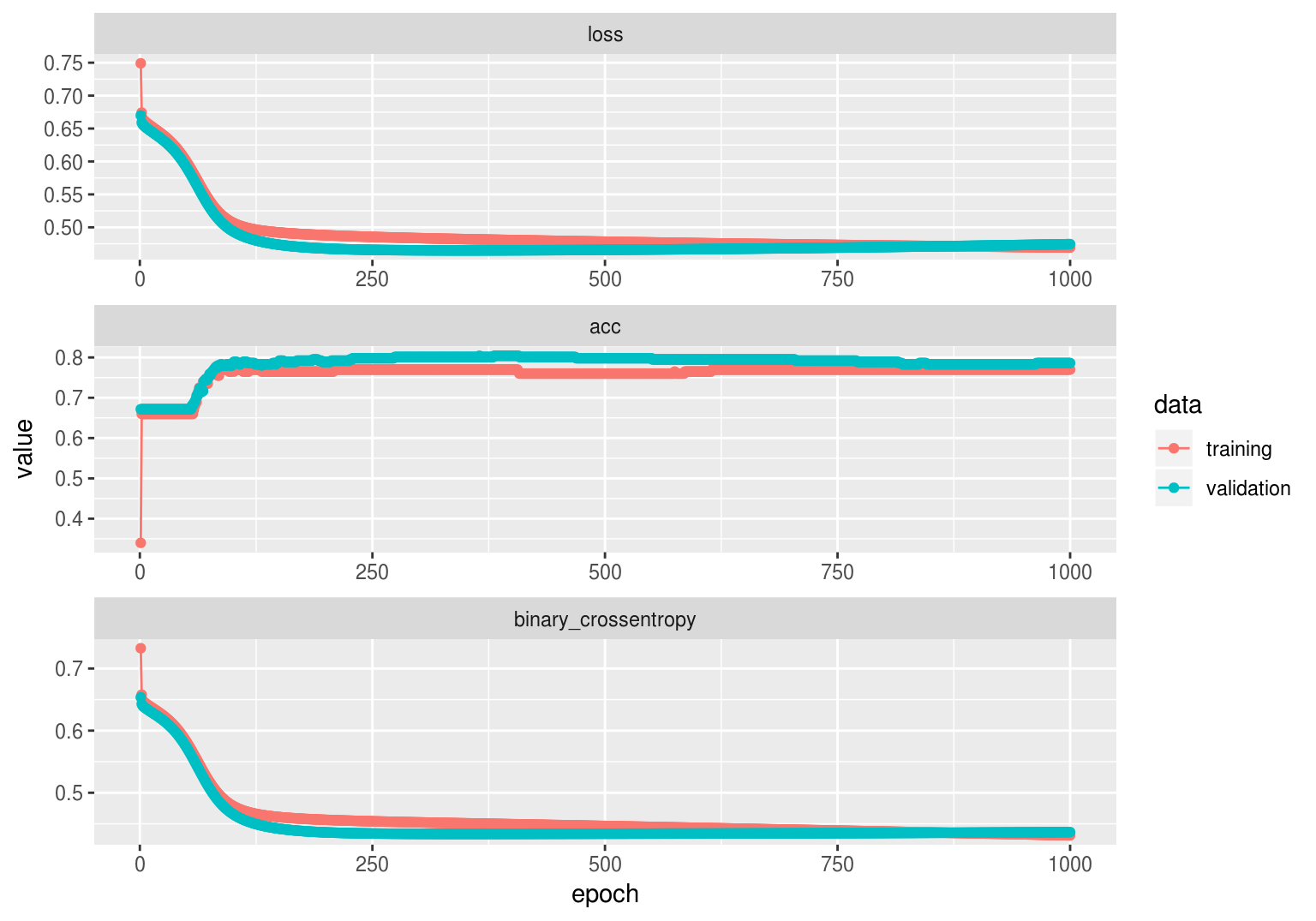

Observación: puedes utilizar Tensorboard, una herramienta para visualizar resultados del entrenamiento de modelos incluída en Tensorflow (que es lo que usa keras para hacer los cálculos):

iteraciones <- modelo_tc %>% fit(
  x_ent_s, y_ent, 
  #batch size mismo que nrow(x_ent_s) es descenso en grad.
  epochs = 500, batch_size = nrow(x_ent_s), 
  verbose = 0,
  callbacks = callback_tensorboard("logs/diabetes/run_1"),
  validation_data = list(x_valid_s, y_valid)
)

y después puedes hacer:

tensorboard("logs/diabetes/")

Ejercicio

Corre el ejemplo anterior con distintos parámetros de tasa de aprendizaje, número de unidades en las capas de intermedia y regularización (cambia arriba verbose=1 para monitorear al correr).

Aprendizaje de máquina

Clase 7 Redes neuronales (parte 1)

7.1 Introducción a redes neuronales

¿Cómo construyen entradas las redes neuronales?

¿Cómo ajustar los parámetros?

7.1.0.1 Ejercicio

7.2 Interacciones en redes neuronales

7.3 Cálculo en redes: feed-forward

Notación

Ejemplo

Ejemplo

7.4 Feed forward

7.5 Backpropagation: cálculo del gradiente (clasificación binaria)

7.5.1 Cálculo para un caso de entrenamiento

Paso 1: Derivar respecto a capa \(l+1\)

Paso 2: Obtener fórmula recursiva

Paso 3: Simplificación de la recursión

Paso 4: Condiciones inciales

Paso 5: Cálculo de parciales

Paso 6: Versión matricial

7.5.2 Algoritmo de backpropagation

7.6 Ajuste de parámetros (introducción)

7.6.1 Ejemplo

Ejercicio