Clase 4 Más sobre problemas de clasificación

En esta parte presentamos técnicas adicionales para evaluar el desempeño de un modelo. En la parte anterior vimos que

  • La devianza es una buena medida para ajustar y evaluar el desempeño de un modelo y comparar modelos, y utiliza las probabilidades de clase. Sin embargo, es una medida de dificil de interpretar en cuanto a los errores que podemos esperar del modelo.

  • Por otro lado, la tasa de clasificación incorrecta puede usarse para evaluar el desempeño de un clasificador (incluyendo uno derivado de probabilidades de clase), puede interpretarse con facilidad, pero se queda corta en muchas aplicaciones. Una deficiencia grande de esta medida es que, contrario al problema de regresión, hay errores de clasificación que son cualitativamente diferentes.

Ejemplo

  • Por ejemplo, diagnosticar a alguien con una enfermedad cuando no la tiene tiene consecuencias distintas a diagnosticar como libre de enfermedad a alguien que la tiene. Estas consecuencias dependen de cómo son son los tratamientos consecuentes, y de qué tan peligrosa es la enfermedad.

  • Cuando usamos un buscador como Google, es cualitativamente diferente que el buscador omita resultados relevantes a que nos presente resultados irrelevantes.

  • ¿Otros ejemplos?

En general, los costos de los distintos errores son distintos, y en muchos problemas quiséramos entenderlos y controlarlos individualmente. Aunque en teoría podríamos asignar costos a los errores y definir una función de pérdida apropiada, en la práctica esto muchas veces no es tan fácil o deseable. Podemos, sin embargo, reportar el tipo de errores que ocurren

Matriz de confusión. Sea \(\hat{G}\) un clasificador. La matriz de confusión \(C\) de \(\hat{G}\) está dada por \(C_{i,j} =\) número de casos de la clase verdadera \(j\) que son clasificados como clase \(i\) por el clasificador

Ejemplo

En un ejemplo de tres clases, podríamos obtener la matriz de confusión:

A B C
A.pred 50 2 0
B.pred 20 105 10
C.pred 20 10 30

Esto quiere decir que de 90 casos de clase \(A\), sólo clasificamos a 50 en la clase correcta, de 117 casos de clase \(B\), acertamos en 105, etcétera. Podemos ver esta tabla de distintas formas, por ejemplo, usando porcentajes por columna, nos dice cómo se distribuyen los casos de cada clase:

knitr::kable(round(prop.table(tabla_1, 2),2))
A B C
A.pred 0.56 0.02 0.00
B.pred 0.22 0.90 0.25
C.pred 0.22 0.09 0.75

Mientras que una tabla de porcentajes por renglón nos muestra qué pasa cada vez que hacemos una predicción dada:

knitr::kable(round(prop.table(tabla_1, 1),2))
A B C
A.pred 0.96 0.04 0.00
B.pred 0.15 0.78 0.07
C.pred 0.33 0.17 0.50

Ahora pensemos cómo podría sernos de utilidad esta tabla. Discute

  • El clasificador fuera uno de severidad de emergencias en un hospital, donde A=requiere atención inmediata B=urgente C=puede posponerse.

  • El clasificador fuera de tipos de cliente de un negocio. Por ejemplo, A = cliente de gasto alto, B=cliente medio, C=abandonador. Imagínate que tiene un costo intentar conservar a un abandonador, y hay una inversión alta para tratar a los clientes A.

La tasa de incorrectos es la misma en los dos ejemplos, pero la adecuación del clasificador es muy diferente.

4.1 Análisis de error para clasificadores binarios

Cuando la variable a predecir es binaria (dos clases), podemos etiquetar una clase como positiva y otra como negativa. En el fondo no importa cómo catalogemos cada clase, pero para problemas particulares una asignación puede ser más natural. Por ejemplo, en diagnóstico de enfermedades, positivo=tiene la enfermedad, en análisis de crédito, positivo=cae en impago, en sistemas de recomendacion, positivo = le gusta el producto X, en recuperación de textos, positivo=el documento es relevante a la búsqueda, etc.

Hay dos tipos de errores en un clasificador binario (positivo - negativo):

  • Falsos positivos (fp): clasificar como positivo a un caso negativo.
  • Falsos negativos (fn): clasificar como negativo a un caso positivo.
A los casos clasificados correctamente les llamamos positivos verdaderos (pv) y negativos verdaderos (nv).

La matriz de confusion es entonces

tabla <- data_frame(' ' = c('positivo.pred','negativo.pred','total'),
                    'positivo'=c('vp','fn','pos'),
                    'negativo'=c('fp','nv','neg'),
                    'total' = c('pred.pos','pred.neg',''))
knitr::kable(tabla)
pos itivo neg ativo tot al
positivo.pred vp fp pred.pos
negativo.pred fn nv pred.neg
total pos neg

Nótese que un clasificador bueno, en general, es uno que tiene la mayor parte de los casos en la diagonal de la matriz de confusión.

Podemos estudiar a nuestro clasificador en términos de las proporciones de casos que caen en cada celda, que dependen del desempeño del clasificador en cuanto a casos positivos y negativos. La nomenclatura puede ser confusa, pues en distintas áreas se usan distintos nombres para estas proporciones:

  • Tasa de falsos positivos \[\frac{fp}{fp+nv}=\frac{fp}{neg}\]

  • Tasa de falsos negativos \[\frac{fn}{pv+fn}=\frac{fn}{pos}\]

  • Especificidad \[\frac{vn}{fp+vn}=\frac{vn}{neg}\]

  • Sensibilidad o Recall \[\frac{vp}{vp+fn}=\frac{vp}{pos}\]

Y también otras que tienen como base las predicciones:

  • Valor predictivo positivo o Precisión \[\frac{vp}{vp+fp}=\frac{vp}{pred.pos}\]

  • Valor predictivo negativo \[\frac{vn}{fn+vn}=\frac{vn}{pred.neg}\]

Dependiendo de el tema y el objetivo hay medidas más naturales que otras:

  • En estadística muchas veces se usa sensibilidad (recall) y especificidad (proporción de positivos que detectamos y proporción de negativos que descartamos). Por ejemplo, si se tratara de una prueba para detectar riesgo de una enfermedad, sensibilidad nos dice qué porcentaje de los casos riesgosos estamos capturando (sensibilidad), y especificidad nos dice qué tan bien excluimos a los casos no riesgosos (especificidad). Estas dos medidas muestran directamente como el clasificador discrimina entre positivos y entre negativos.

  • En búsqueda y recuperación de documentos o imagenes, o detección de fraude ( donde positivo = el documento es relevante / la transacción es fraudulenta y negativo = el documento no es relevante / transacción normal), se usa más comunmente precisión y recall. Esto es porque nos interesa saber de todos los resultados con predicción positiva (documentos o imagenes recuperadas), qué porcentaje son relevantes (precisión), y también, de todos los documentos relevantes (positivos), cuáles son recuperados (recall).

Pero tiende a considerarse que especificidad o tasas de falsos positivos es menos útil, pues estas son cantidades dependen de una gran cantidad de documentos o transacciones irrelevantes, y tienden a ser cercanas a 1 para cualquier clasificador razonable (¿por qué?).

Cada clasificador tiene un balance distinto especificidad-sensibliidad. Muchas veces no escogemos clasificadores por la tasa de incorrectos solamente, sino que intentamos buscar un balance adecuado entre el comportamiento de clasificación para positivos y para negativos.

Medidas resumen de desempeño

La primera medida resumen que vimos es el error de clasificación, que no toma en cuenta el tipo de errores:

  • Tasa de clasificación incorrecta \[\frac{fn+fv}{neg+pos}\] Y existen otras medidas que intentan resumir los dos tipos de errores de distinta manera, como

  • Medida F (media armónica de precisión y recall) \[2\frac{precision \cdot recall}{precision + recall}\] Se usa la la media armónica que penaliza más fuertemente desempeño malo en alguna de nuestras dos medidas (precisión y recall) que el promedio armónico.

Ejemplo

Si precision = 0.01 (muy malo) y recall = 1 (excelente), o recall=0.01 y precisión = 1 (excelente), la media usual considera igual de buenos estos dos clasificadores. A su vez, estos dos se califican similar a un clasificador con precision = 0.5 y recall = 0.5. Sin embargo, la media armónica (F) da un score mucho más bajo a los primeros dos clasificadores:

media_armonica <- function(x){
    1/mean(1/x)
}
media_armonica(c(0.01, 1))
## [1] 0.01980198
media_armonica(c(0.5, 0.5))
## [1] 0.5
  • AUC (area bajo la curva ROC) que veremos más adelante.

Interpetación de resúmenes de desempeño y tasas base

Cuando consideramos las tasas de desempeño de un clasificador debemos comparar con lo que sucedería si no usáramos el clasificador (si no usáramos datos). Una manera de hacer esto consiste en utilizar el clasificador base:

  • Clasificar todo como negativo (o positivo)

Ejemplo

Consideramos un problema donde tenemos 20% de positivos y 80% de negativos en una población. ¿Cuál es el desempeño de estos clasificadores base? Podemos usar la ecuación

\[P(acertar) = P(acertar|pos)P(pos) + P(acertar|neg)P(neg)\] que en este caso es:

\[P(acertar) = 0.2P(acertar|pos) + 0.8 P(acertar|neg)\]

  • Si clasificamos siempre a positivo, la tasa de correctos será de 20%, pues \(P(acertar|pos) = 1\) y \(P(acertar|neg)= 0\)
  • Si clasificamos siempre a negativo, la tasa de correctos será de 80%, pues \(P(acertar|pos) = 0\) y \(P(acertar|neg)= 1\)

En este ejemplo, si tuviéramos un clasificador con una tasa de correctos de \(75\%\), querría decir que no logramos mucho en el sentido de la certeza de nuestra predicción.

Comparamos la tasa de correctos de clasificadores contra la tasa base \(\max\{p_{pos}, 1- p_{pos}\}\), donde \(p_{pos}\) es la tasa de positivos en nuestros datos.

Típicamente esperamos superar esta tasa de correctos base. Nota: cuando los costos de los distintos errores son muy diferentes, existen otras medidas más apropiadas

Ejercicio

Calcular la matriz de confusión (sobre la muestra de prueba) para el clasificador logístico de diabetes en términos de glucosa. Calcula adicionalmente con la muestra de prueba sus valores de especificidad y sensibilidad, y precisión y recall.

diabetes_ent <- as_data_frame(MASS::Pima.tr)
diabetes_pr <- as_data_frame(MASS::Pima.te)
mod_1 <- glm(type ~ glu, data = diabetes_ent, family = 'binomial')
preds_prueba <- predict(mod_1, newdata = diabetes_pr, type ='response')
# rellena esta linea en términos de preds_prueba
# clase_pred <- 
# table(clase_pred)
# ahora calcula la matriz de confusión
# table()
# Usando esta tabla encuentra 
# tasa de incorrectos especificidad y sensibilidad, precisión y recall.

4.1.1 Puntos de corte para un clasificador binario

¿Qué sucede cuando el perfil de sensibilidad y especificidad de un clasificador binario no es apropiado para nuestros fines? Recordemos que una vez que hemos estimado con \(\hat{p}_1(x)\), nuestra regla de clasificación es:

  1. Predecir positivo si \(\hat{p}_1(x) > 0.5\),
  2. Predecir negativo si \(\hat{p}_1(x) \leq 0.5.\)

Esto sugiere una regla alternativa:

Para \(0 < d < 1\), podemos utilizar nuestras estimaciones \(\hat{p}_1(x)\) para construir un clasificador alternativo poniendo:

  1. Predecir positivo si \(\hat{p}_1(x) > d\),
  2. Predecir negativo si \(\hat{p}_1(x) \leq d\).

Distintos valores de \(d\) dan distintos perfiles de sensibilidad-especificidad para una misma estimación de las probabilidades condicionales de clase: Para minimizar la tasa de incorrectos conviene poner \(d = 0.5\). Sin embargo, es común que este no es el único fin de un clasificador bueno (pensar en ejemplo de fraude).

  • Cuando incrementamos d, quiere decir que exigimos estar más seguros de que un caso es positivo para clasificarlo como positivo. Eso quiere decir que la especifidad va a ser más grande (entre los negativos verdaderos va a haber menos falsos positivos). Sin embargo, la sensibilidad va a ser más chica pues captamos menos de los verdaderos positivos.

Ejemplo

Por ejemplo, si en el caso de diabetes incrementamos el punto de corte a 0.7:

table(preds_prueba > 0.7, diabetes_pr$type)
##        
##          No Yes
##   FALSE 220  77
##   TRUE    3  32
tab <- prop.table(table(preds_prueba > 0.7, diabetes_pr$type), 2)
tab
##        
##                 No        Yes
##   FALSE 0.98654709 0.70642202
##   TRUE  0.01345291 0.29357798

La especificidad ahora 0.99 , muy alta (descartamos muy bien casos negativos), pero la sensibilidad se deteriora a 0.29

  • Cuando hacemos más chico d, entonces exigimos estar más seguros de que un caso es negativo para clasificarlo como negativo. Esto aumenta la sensibilidad, pero la especificidad baja. Por ejemplo, si en el caso de diabetes ponemos el punto de corte en 0.3:
table(preds_prueba > 0.3, diabetes_pr$type)
##        
##          No Yes
##   FALSE 170  37
##   TRUE   53  72
tab <- prop.table(table(preds_prueba > 0.3, diabetes_pr$type),2)
tab
##        
##                No       Yes
##   FALSE 0.7623318 0.3394495
##   TRUE  0.2376682 0.6605505

Ejemplo

Podemos tener una intuición de cómo cambian las tasas de error dependiendo de donde cortamos mostrando la tabla ordenada por probabilidades estimadas (incluimos también las covariables para entender qué variables están más correlacionadas con las probabilidades):

library(tabplot)
mod_1 <- glm(type ~ glu, diabetes_ent, family = 'binomial')
diabetes_pr$probs_prueba_1 <- predict(mod_1, newdata = diabetes_pr,
                                      type = "response") 
head(arrange(diabetes_pr, desc(probs_prueba_1)))
## # A tibble: 6 x 9
##   npreg   glu    bp  skin   bmi   ped   age type  probs_prueba_1
##   <int> <int> <int> <int> <dbl> <dbl> <int> <fct>          <dbl>
## 1     2   197    70    45  30.5 0.158    53 Yes            0.874
## 2     4   197    70    39  36.7 2.33     31 No             0.874
## 3     8   196    76    29  37.5 0.605    57 Yes            0.870
## 4     1   196    76    36  36.5 0.875    29 Yes            0.870
## 5     3   193    70    31  34.9 0.241    25 Yes            0.857
## 6     5   189    64    33  31.2 0.583    29 Yes            0.837
tableplot(diabetes_pr, sortCol = probs_prueba_1)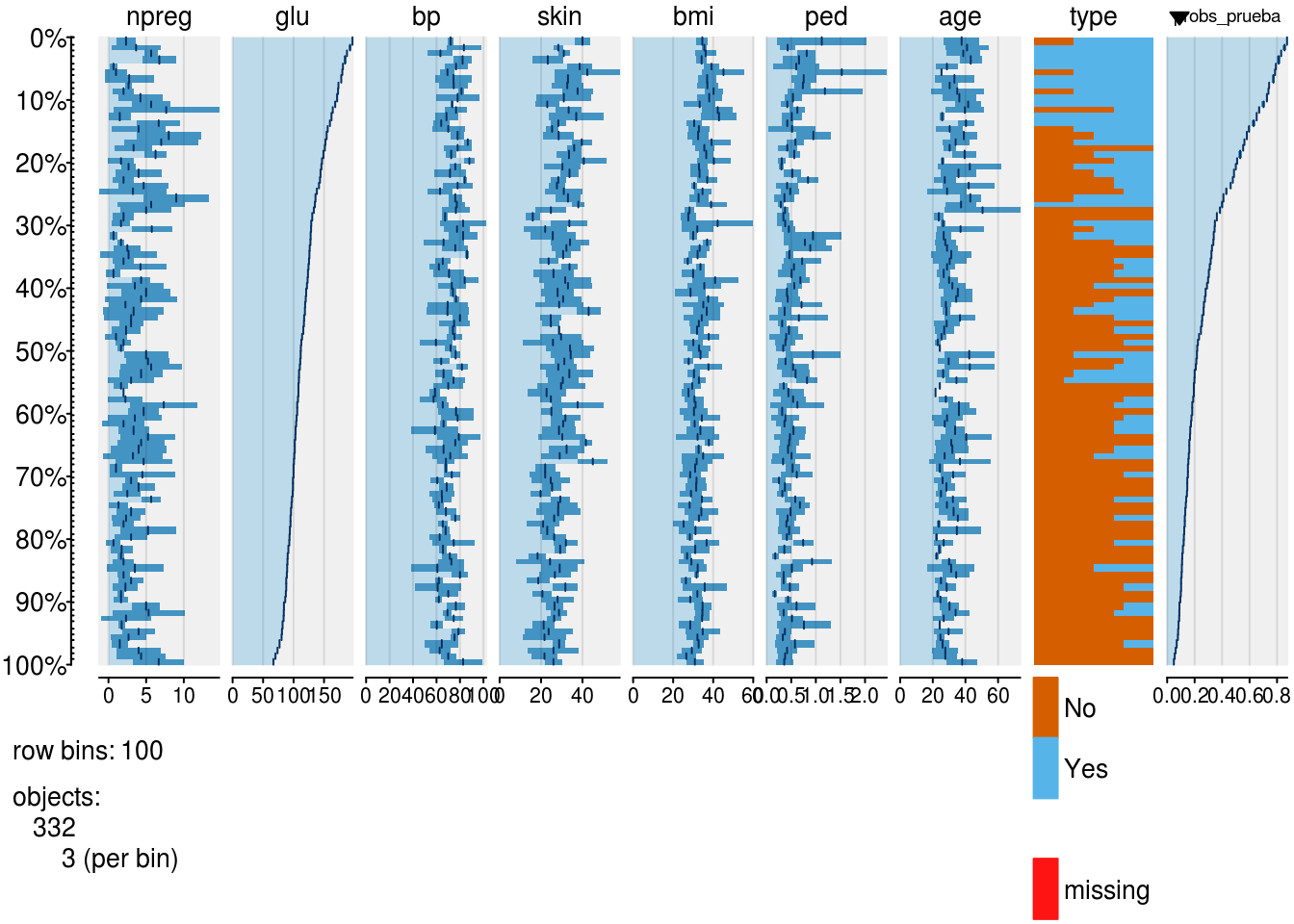

La columna de probabilidad de la derecha nos dice en qué valores podemos cortar para obtener distintos clasificadores. Nótese que si cortamos más arriba, se nos escapan más positivos verdaderos que clasificamos como negativos, pero clasificamos a más negativos verdaderos como negativos. Lo opuesto ocurre cuando cortamos más abajo.

4.1.2 Espacio ROC de clasificadores

Podemos visualizar el desempeño de cada uno de estos clasificadores construidos con puntos de corte mapeándolos a las coordenadas de tasa de falsos positivos (1-especificidad) y sensibilidad:

clasif_1 <- data.frame(
  corte = c('0.3','0.5','0.7','perfecto','azar'),
  tasa_falsos_pos=c(0.24,0.08,0.02,0,0.7),
  sensibilidad =c(0.66, 0.46,0.19,1,0.7))
ggplot(clasif_1, aes(x=tasa_falsos_pos, y=sensibilidad,
  label=corte)) + geom_point() + 
  geom_abline(intercept=0, slope=1) +
  xlim(c(0,1)) +ylim(c(0,1)) + geom_text(hjust=-0.3, col='red')+
  xlab('1-especificidad (tasa falsos pos)')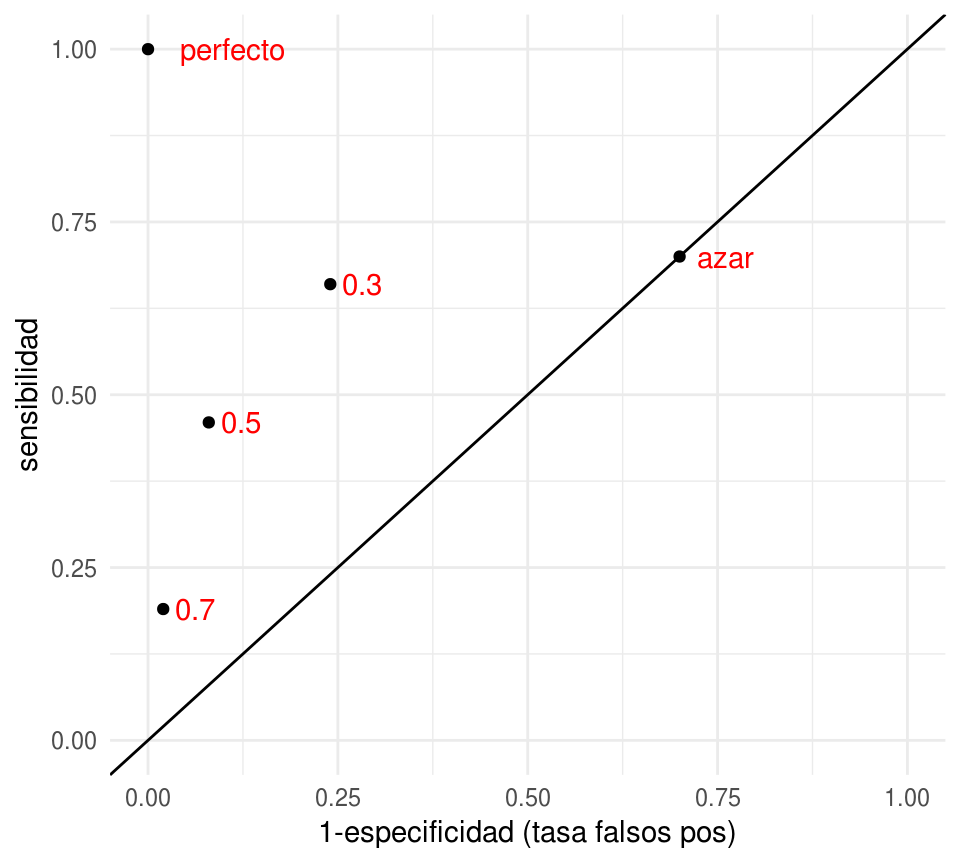

  1. Nótese que agregamos otros dos clasificadores, uno perfecto, que tiene tasa de falsos positivos igual a 0 y sensibilidad igual a 1.
  2. En esta gráfica, un clasificador \(G_2\) que está arriba a la izquierda de \(G_1\) domina a \(G_1\), pues tiene mejor especificidad y mejor sensibilidad. Entre los clasificadores 0.3, 0.5 y 0.7 de la gráfica, no hay ninguno que domine a otro.
  3. Todos los clasificadores en la diagonal son equivalentes a un clasificador al azar. ¿Por qué? La razón es que si cada vez que vemos un nuevo caso lo clasificamos como positivo con probabilidad \(p\) fija y arbitraria. Esto implica que cuando veamos un caso positivo, la probabilidad de ’atinarle’ es de p (sensibilidad), y cuando vemos un negativo, la probabilidad de equivocarnos también es de 1-p (tasa de falsos positivos), por lo que la espcificidad es p también. De modo que este clasificador al azar está en la diagonal.
  4. ¿Qué podemos decir acerca de clasificadores que caen por debajo de la diagonal? Estos son clasificadores particularmente malos, pues existen clasificadores con mejor especificidad y/o sensibilidad que son clasificadores al azar! Sin embargo, se puede construir un mejor clasificador volteando las predicciones, lo que cambia sensibilidad por tasa de falsos positivos.
  5. ¿Cuál de los tres clasificadores es el mejor? En términos de la tasa de incorrectos, el de corte 0.5. Sin embargo, para otros propósitos puede ser razonable escoger alguno de los otros.

4.2 Perfil de un clasificador binario y curvas ROC

En lugar de examinar cada punto de corte por separado, podemos hacer el análisis de todos los posibles puntos de corte mediante la curva ROC (receiver operating characteristic, de ingeniería).

Para un problema de clasificación binaria, dadas estimaciones \(\hat{p}(x)\), la curva ROC grafica todos los pares de (1-especificidad, sensibilidad) para cada posible punto de corte \(\hat{p}(x) > d\).

Vamos a graficar todos los pares (1-especificidad, sensibilidad) para cada punto de corte \(d\) de estas probabilidades.

library(ROCR)
pred_rocr <- prediction(diabetes_pr$probs_prueba_1, diabetes_pr$type) 
perf <- performance(pred_rocr, measure = "sens", x.measure = "fpr") 
graf_roc_1 <- data_frame(tfp = perf@x.values[[1]], sens = perf@y.values[[1]], 
                       d = perf@alpha.values[[1]])

ggplot(graf_roc_1, aes(x = tfp, y = sens, colour=d)) + geom_point() +
  xlab('1-especificidad') + ylab('Sensibilidad')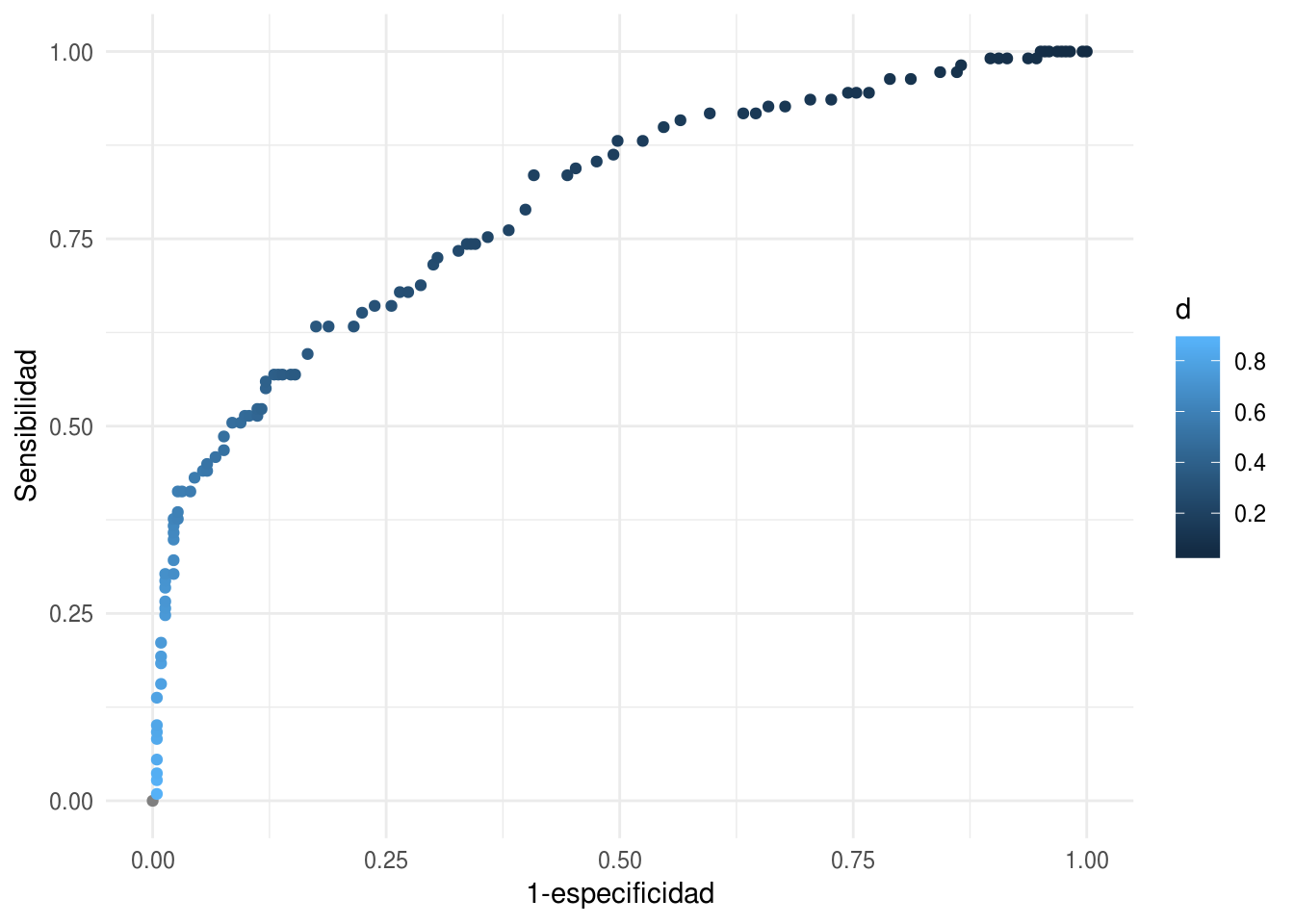

En esta gráfica podemos ver todos los clasificadores posibles basados en las probabilidades de clase. Podemos usar estas curvas como evaluación de nuestros clasificadores, dejando para más tarde la selección del punto de corte, si esto es necesario (por ejemplo, dependiendo de los costos de cada tipo de error).

También podemos definir una medida resumen del desempeño de un clasificador según esta curva:

La medida AUC (area under the curve) para un clasificador es el área bajo la curva generada por los pares sensibilidad-especificidad de la curva ROC. 
auc_1 <- performance(pred_rocr, measure = 'auc')@y.values
auc_1[[1]]
## [1] 0.7970543

También es útil para comparar modelos. Consideremos el modelo de los datos de diabetes que incluyen todas las variables:

mod_2 <- glm(type ~ ., diabetes_ent, family = 'binomial')
diabetes_pr$probs_prueba_2 <- predict(mod_2, newdata = diabetes_pr,
                                      type = "response") 
head(arrange(diabetes_pr, desc(probs_prueba_2)))
## # A tibble: 6 x 10
##   npreg   glu    bp  skin   bmi   ped   age type  probs_prueba_1
##   <int> <int> <int> <int> <dbl> <dbl> <int> <fct>          <dbl>
## 1     0   180    78    63  59.4 2.42     25 Yes            0.785
## 2     4   197    70    39  36.7 2.33     31 No             0.874
## 3     5   187    76    27  43.6 1.03     53 Yes            0.827
## 4     3   173    82    48  38.4 2.14     25 Yes            0.737
## 5     0   173    78    32  46.5 1.16     58 No             0.737
## 6    17   163    72    41  40.9 0.817    47 Yes            0.658
## # ... with 1 more variable: probs_prueba_2 <dbl>
tableplot(diabetes_pr, sortCol = probs_prueba_2)

Y graficamos juntas:

library(ROCR)
pred_rocr <- prediction(diabetes_pr$probs_prueba_2, diabetes_pr$type) 
perf <- performance(pred_rocr, measure = "sens", x.measure = "fpr") 
auc_2 <- performance(pred_rocr, measure = "auc")@y.values
graf_roc_2 <- data_frame(tfp = perf@x.values[[1]], sens = perf@y.values[[1]], 
                       d = perf@alpha.values[[1]])

graf_roc_2$modelo <- 'Todas las variables'
graf_roc_1$modelo <- 'Solo glucosa'
graf_roc <- bind_rows(graf_roc_1, graf_roc_2)

ggplot(graf_roc, aes(x = tfp, y = sens, colour = modelo)) + geom_point() +
  xlab('1-especificidad') + ylab('Sensibilidad')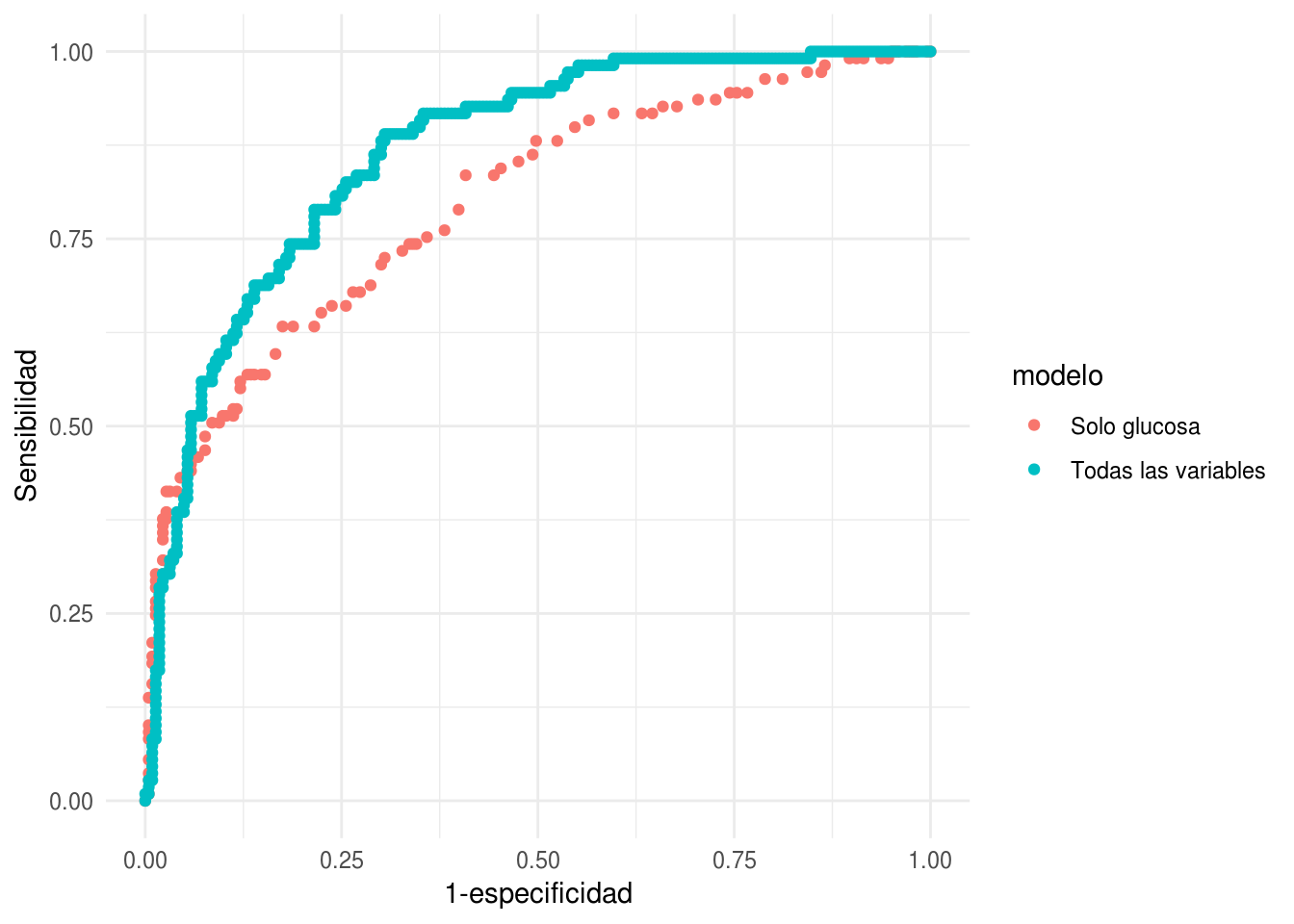

Comparación auc:

auc_1
## [[1]]
## [1] 0.7970543
auc_2
## [[1]]
## [1] 0.8658823

En este ejemplo, vemos que casi no importa que perfil de especificidad y sensibilidad busquemos: el clasificador que usa todas las variables domina casi siempre al clasificador que sólo utiliza las variables de glucosa. La razón es que para cualquier punto de corte (con sensibilidad menor a 0.4) en el clasificador de una variable, existe otro clasificador en la curva roja (todas las variable), que domina al primero. La excepción es para clasificadores de valores de sensibilidad baja, con tasas de falsos positivos muy chicas: en este caso, el modelo de una variable puede ser ligeramente superior.

4.3 Regresión logística para problemas de más de 2 clases

Consideramos ahora un problema con más de dos clases, de manera que \(G ∈ {1,2,...,K}\) (\(K\) clases), y tenemos \(X = (X1 ...,Xp)\) entradas. ¿Cómo generalizar el modelo de regresión logística para este problema? Una estrategia es la de uno contra todos:

En clasificación uno contra todos, hacemos

  1. Para cada clase \(g\in\{1,\ldots,K\}\) entrenamos un modelo de regresión logística (binaria) \(\hat{p}^{(g)}(x)\), tomando como positivos a los casos de 1 clase \(g\), y como negativos a todo el resto. Esto lo hacemos como en las secciones anteriores, y de manera independiente para cada clase.

  2. Para clasificar un nuevo caso \(x\), calculamos \[\hat{p}^{(1)}, \hat{p}^{(2)},\ldots, \hat{p}^{(K)}\]

y clasificamos a la clase de máxima probabilidad \[\hat{G}(x) = \arg\max_g \hat{p}^{(g)}(x)\] Nótese que no hay ninguna garantía de que las probabilidades de clase sumen 1, pues se trata de estimaciones independientes de cada clase. En este sentido, produce estimaciones que en realidad no satisfacen las propiedades del modelo de probabilidad establecido - aunque pueden normalizarse. Sin embargo, esta estrategia es simple y en muchos casos funciona bien.

4.3.1 Regresión logística multinomial

Si queremos obtener estimaciones de las probabilidades de clase que sumen uno, entonces tenemos que contruir las estimaciones de cada clase de clase de manera conjunta. Como vimos antes, tenemos que estimar, para cada \(x\) y \(g\in\{1,\ldots, K\}\), las probabilidades condicionales de clase: \[p_g(x) = P(G = g|X = x).\]

Consideremos primero cómo funciona el modelo de regresión logística (2 clases)

Tenemos que \[p_1(x) = h(\beta_0 + \beta_1x_1 + \ldots + \beta_p x_p) = \exp(\beta_0 + \beta_1x_1 + \ldots + \beta_p x_p)/Z \] y \[p_2 (x) = 1/Z\] donde \(Z = 1 + \exp(\beta_0 + \beta_1x_1 + \ldots + \beta_p x_p)\).

Podemos generalizar para más de 2 clases usando una idea similar. Cada clase tiene su juego de coeficientes:

\[p_1(x) = \exp(\beta_{0,1} + \beta_{1,1}x_1 + \ldots + \beta_{p,1} x_p)/Z\]

\[p_2(x) = \exp(\beta_{0,2} + \beta_{1,2}x_2 + \ldots + \beta_{p.2} x_p)/Z\] hasta \[p_{K-1}(x) = \exp(\beta_{0,{K-1}} + \beta_{1,{K-1}}x_2 + \ldots + \beta_{p,{K-1}} x_p)/Z\] y \[p_K(x) = 1/Z\]

En este caso, para que las probabilidades sumen 1, necesitamos que \[Z = 1 + \sum_{j=1}^{K-1}\exp(\beta_0^j + \beta_1^jx_1 + \ldots + \beta_p^j x_p)\]

Para ajustar coeficientes, usamos el mismo criterio de devianza de entrenamiento. Buscamos minimizar: \[D(\beta)=−2 \sum_{i=1}^N \log p_{g^{(i)}}(x^{(i)}),\] Donde \(\beta\) contiene todos los coeficientes organizados en un vector de tamaño \((p+1)(K-1)\): \[\beta = ( \beta_0^1, \beta_1^1, \ldots , \beta_p^1, \beta_0^2, \beta_1^2, \ldots , \beta_p^2, \ldots \beta_0^{K-1}, \beta_1^{K-1}, \ldots , \beta_p^{K-1} )\]

Y ahora podemos usar algún método númerico para minimizar la devianza (por ejemplo, descenso en gradiente). Cuando es muy importante tener probabilidades bien calibradas, el enfoque multinomial es más apropiado, pero muchas veces, especialmente si sólo nos interesa clasificar, los dos métodos dan resultados similares.

4.3.2 Interpretación de coeficientes

Los coeficientes mostrados en la parametrización de arriba se intrepretan más fácilmente como comparaciones de la clase \(g\) contra la clase \(K\), pues

\[\log\left (\frac{p_g(x)}{p_K(x)}\right ) = \beta_{0,{g}} + \beta_{1,{g}}x_1 + \ldots + \beta_{p,{g}} x_p\]

Para comparar la clase \(j\) con la clase \(k\) notamos que

\[\log\left (\frac{p_j(x)}{p_k(x)}\right ) = (\beta_{0,{j}}- \beta_{0,{k}}) + (\beta_{1,{j}}-\beta_{1,{k}} )x_1 + \ldots + (\beta_{p,{j}} -\beta_{p,{k}}) x_p\]

Así que sólo hace falta restar los coeficientes. Nótese adicionalmente que en la parametrización, podemos pensar que

\[\beta_{0,K} = \beta_{1,K} = \cdots = \beta_{p,K} = 0\]

4.3.3 Ejemplo: Clasificación de dígitos con regresión multinomial

digitos_entrena <- read_csv('datos/zip-train.csv')
## Parsed with column specification:
## cols(
##   .default = col_double()
## )
## See spec(...) for full column specifications.
digitos_prueba <- read_csv('datos/zip-test.csv')
## Parsed with column specification:
## cols(
##   .default = col_double()
## )
## See spec(...) for full column specifications.
names(digitos_entrena)[1] <- 'digito'
names(digitos_entrena)[2:257] <- paste0('pixel_', 1:256)
names(digitos_prueba)[1] <- 'digito'
names(digitos_prueba)[2:257] <- paste0('pixel_', 1:256)

En este ejemplo, usamos la función multinom de nnet, que usa BFGS para hacer la optimización:

library(nnet)
mod_mult <- multinom(digito ~ ., data = digitos_entrena, MaxNWt=100000, maxit = 20)
## # weights:  2580 (2313 variable)
## initial  value 16788.147913 
## iter  10 value 2598.959017
## iter  20 value 1494.978090
## final  value 1494.978090 
## stopped after 20 iterations

Checamos para diagnóstico la matriz de confusión de entrenamiento.

table(predict(mod_mult), digitos_entrena$digito)
##    
##        0    1    2    3    4    5    6    7    8    9
##   0 1153    0    5    2    3    9    1    1    7    0
##   1    0  998    0    0    2    0    1    1    2    3
##   2    2    0  693    1    7    2    8    3   10    2
##   3    9    0   15  632    2   21    0    2   24    2
##   4    3    2    9    2  621    4    4    9   10   44
##   5   24    4    5   19    9  511   43    1   34    6
##   6    2    0    0    0    1    3  607    0    0    0
##   7    0    0    1    0    0    1    0  613    1    8
##   8    1    1    3    2    2    4    0    1  451    2
##   9    0    0    0    0    5    1    0   14    3  577

Ahora validamos con la muestra de prueba y calculamos error de clasificación:

confusion_prueba <- table(predict(mod_mult, newdata = digitos_prueba), digitos_prueba$digito)
confusion_prueba
##    
##       0   1   2   3   4   5   6   7   8   9
##   0 335   0   3   0   3   6   4   0   3   0
##   1   0 252   0   0   1   0   0   0   1   3
##   2   1   1 171   4   8   0   5   2   3   2
##   3   3   3   8 145   1  18   0   3  12   0
##   4   3   6   7   1 176   1   2   6   8  16
##   5  11   1   5  13   2 130  13   2  14   1
##   6   4   1   1   0   2   0 143   0   1   0
##   7   0   0   1   1   2   1   0 130   1   5
##   8   1   0   2   1   2   1   3   0 118   0
##   9   1   0   0   1   3   3   0   4   5 150
sum(diag(confusion_prueba))/sum(confusion_prueba)
## [1] 0.8719482
round(prop.table(confusion_prueba, 2),2)
##    
##        0    1    2    3    4    5    6    7    8    9
##   0 0.93 0.00 0.02 0.00 0.02 0.04 0.02 0.00 0.02 0.00
##   1 0.00 0.95 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.02
##   2 0.00 0.00 0.86 0.02 0.04 0.00 0.03 0.01 0.02 0.01
##   3 0.01 0.01 0.04 0.87 0.00 0.11 0.00 0.02 0.07 0.00
##   4 0.01 0.02 0.04 0.01 0.88 0.01 0.01 0.04 0.05 0.09
##   5 0.03 0.00 0.03 0.08 0.01 0.81 0.08 0.01 0.08 0.01
##   6 0.01 0.00 0.01 0.00 0.01 0.00 0.84 0.00 0.01 0.00
##   7 0.00 0.00 0.01 0.01 0.01 0.01 0.00 0.88 0.01 0.03
##   8 0.00 0.00 0.01 0.01 0.01 0.01 0.02 0.00 0.71 0.00
##   9 0.00 0.00 0.00 0.01 0.02 0.02 0.00 0.03 0.03 0.85

El resultado no es muy bueno. Veremos más adelante mejores métodos para este problema. ¿Podemos interpretar el modelo?

Una idea es tomar los coeficientes y graficarlos según la estructura de las imágenes:

coefs <- coef(mod_mult)
coefs_reng <- coefs[1, , drop =FALSE]
coefs <- rbind(coefs_reng, coefs)
coefs[1 , ] <- 0
dim(coefs)
## [1]  10 257
beta_df <- coefs[,-1] %>% as.data.frame %>% 
  mutate(digito = 0:(nrow(coefs)-1)) %>%
  gather(pixel, valor, contains('pixel')) %>%
  separate(pixel, into = c('str','pixel_no'), sep='_') %>%
  mutate(x = (as.integer(pixel_no)-1) %% 16, y = -((as.integer(pixel_no)-1) %/% 16))
head(beta_df)
##   digito   str pixel_no        valor x y
## 1      0 pixel        1  0.000000000 0 0
## 2      1 pixel        1  0.621681333 0 0
## 3      2 pixel        1 -0.005914605 0 0
## 4      3 pixel        1  0.044257959 0 0
## 5      4 pixel        1  0.190966643 0 0
## 6      5 pixel        1 -0.010655932 0 0

Podemos cruzar la tabla con sí misma para hacer comparaciones de cómo discrimina el modelo entre cada par de dígitos:

tab_coef <- beta_df %>% select(digito, x, y, valor)
tab_coef_1 <- tab_coef
names(tab_coef_1) <- c('digito_1','x','y','valor_1')
tab_cruzada <- full_join(tab_coef_1, tab_coef) %>% mutate(dif = valor_1 - valor)
## Joining, by = c("x", "y")
tab_cruzada <- tab_cruzada %>% group_by(digito, digito_1) %>% 
  mutate(dif_s = (dif - mean(dif))/sd(dif)) %>%
  mutate(dif_p = pmin(pmax(dif_s, -2), 2))
ggplot(tab_cruzada, aes(x=x, y=y)) + geom_tile(aes(fill = dif_p)) + 
  facet_grid(digito_1~digito) + scale_fill_distiller(palette = "Spectral")

Discusión

Nótese que no corrimos el modelo hasta convergencia. Vamos a hacerlo ahora:

mod_mult <- multinom(digito ~ ., data = digitos_entrena, MaxNWt=100000, maxit = 500)
## # weights:  2580 (2313 variable)
## initial  value 16788.147913 
## iter  10 value 2598.959017
## iter  20 value 1494.978090
## iter  30 value 903.291402
## iter  40 value 443.785686
## iter  50 value 260.626756
## iter  60 value 190.835491
## iter  70 value 160.773160
## iter  80 value 114.048146
## iter  90 value 88.746976
## iter 100 value 76.302570
## iter 110 value 63.400188
## iter 120 value 54.375215
## iter 130 value 46.291174
## iter 140 value 38.303470
## iter 150 value 28.822810
## iter 160 value 17.888648
## iter 170 value 9.531256
## iter 180 value 2.985614
## iter 190 value 0.714996
## iter 200 value 0.209654
## iter 210 value 0.066710
## iter 220 value 0.030412
## iter 230 value 0.014036
## iter 240 value 0.006702
## iter 250 value 0.004146
## iter 260 value 0.001844
## iter 270 value 0.001128
## iter 280 value 0.000744
## iter 290 value 0.000462
## iter 300 value 0.000308
## iter 310 value 0.000265
## iter 320 value 0.000231
## final  value 0.000076 
## converged
confusion_prueba <- table(predict(mod_mult, newdata = digitos_prueba), digitos_prueba$digito)
confusion_prueba
##    
##       0   1   2   3   4   5   6   7   8   9
##   0 332   0   6   2   4   2   1   2   7   2
##   1   0 242   1   3   3   4   1   2   0   2
##   2   2   2 148   5   5   0   4   3   3   0
##   3   4   1   9 128   4  10   0   3   2   4
##   4   3   5   8   0 149   8   6   7   5   2
##   5   0   1   3  11   5 116   8   0  10   1
##   6   5   7   4   3  10   4 144   0   4   1
##   7   2   1   3   1   4   1   1 125   2   4
##   8   6   3  14   7   6  10   4   0 132   3
##   9   5   2   2   6  10   5   1   5   1 158
sum(diag(confusion_prueba))/sum(confusion_prueba)
## [1] 0.8340807
round(prop.table(confusion_prueba, 2),2)
##    
##        0    1    2    3    4    5    6    7    8    9
##   0 0.92 0.00 0.03 0.01 0.02 0.01 0.01 0.01 0.04 0.01
##   1 0.00 0.92 0.01 0.02 0.02 0.02 0.01 0.01 0.00 0.01
##   2 0.01 0.01 0.75 0.03 0.02 0.00 0.02 0.02 0.02 0.00
##   3 0.01 0.00 0.05 0.77 0.02 0.06 0.00 0.02 0.01 0.02
##   4 0.01 0.02 0.04 0.00 0.74 0.05 0.04 0.05 0.03 0.01
##   5 0.00 0.00 0.02 0.07 0.02 0.72 0.05 0.00 0.06 0.01
##   6 0.01 0.03 0.02 0.02 0.05 0.02 0.85 0.00 0.02 0.01
##   7 0.01 0.00 0.02 0.01 0.02 0.01 0.01 0.85 0.01 0.02
##   8 0.02 0.01 0.07 0.04 0.03 0.06 0.02 0.00 0.80 0.02
##   9 0.01 0.01 0.01 0.04 0.05 0.03 0.01 0.03 0.01 0.89

Y nota que el error es más grande que cuando nos detuvimos antes. Discute en clase:

  • Grafica los coeficientes para este segundo modelo
  • ¿En cuál de los dos modelos es más fácil interpretar los coeficientes? ¿En cuál es menor el error?
  • ¿Cuál crees que es el problema de este segundo modelo comparado con el primero? ¿Por qué crees que sucede? ¿Cómo podríamos corregir este problema?

4.4 Descenso en gradiente para regresión multinomial logística

Supondremos \(K\) clases, numeradas de \(0,1,\ldots, K-1\). OJO: al aplicar este código debes ser cuidadoso con las etiquetas de clase.

pred_multinom <- function(x, beta){
  p <- ncol(x)
  K <- length(beta)/(p+1) + 1
  beta_mat <- matrix(beta, K - 1, p + 1 , byrow = TRUE)
  u_beta <- exp(as.matrix(cbind(1, x)) %*% t(beta_mat))
  Z <- 1 + apply(u_beta, 1, sum)
  p_beta <- cbind(u_beta, 1)/Z
  as.matrix(p_beta)
}

devianza_calc <- function(x, y){
  dev_fun <- function(beta){
    p_beta <- pred_multinom(x, beta)
    p <- sapply(1:nrow(x), function(i) p_beta[i, y[i]+1])
   -2*sum(log(p))
  }
  dev_fun
}

grad_calc <- function(x_ent, y_ent){
  p <- ncol(x_ent)
  K <- length(unique(y_ent)) 
  y_fact <- factor(y_ent) 
  # matriz de indicadoras de clase
  y_dummy <-  model.matrix(~-1 + y_fact)
  salida_grad <- function(beta){
    p_beta <-  pred_multinom(x_ent, beta)
    e_mat <-  (y_dummy  - p_beta)[, -K]
    grad_out <- -2*(t(cbind(1,x_ent)) %*% e_mat)
    as.numeric(grad_out)
  }
  salida_grad
}
descenso <- function(n, z_0, eta, h_deriv, dev_fun){
  z <- matrix(0,n, length(z_0))
  z[1, ] <- z_0
  for(i in 1:(n-1)){
    z[i+1, ] <- z[i, ] - eta * h_deriv(z[i, ])
    if(i %% 100 == 0){
      print(paste0(i, ' Devianza: ', dev_fun(z[i+1, ])))
    }
  }
  z
}
x_ent <- digitos_entrena %>% select(contains('pixel')) %>% as.matrix
y_ent <- digitos_entrena$digito
x_ent_s <- scale(x_ent)
medias <- attr(x_ent_s, 'scaled:center')
sd <- attr(x_ent_s, 'scaled:scale')
x_pr <- digitos_prueba %>% select(contains('pixel')) %>% as.matrix
y_pr <- digitos_prueba$digito
# inicializamos coeficientes al azar
beta <- runif(257*9)
dev_ent <- devianza_calc(x_ent_s, y_ent)
grad <- grad_calc(x_ent_s, y_ent)
dev_ent(beta)
## [1] 244975.6

Hacemos algunas revisiones del gradiente:

beta_2 <- beta 
epsilon <- 0.00001
beta_2[1000] <- beta[1000] + epsilon

(dev_ent(beta_2) - dev_ent(beta))/epsilon
## [1] -920.3948
grad(beta)[1000]
## [1] -920.3967

Ya ahora podemos hacer descenso:

iteraciones <- descenso(2000, rep(0, 257*9), eta=0.001, 
                        h_deriv = grad, dev_fun = dev_ent)
## [1] "100 Devianza: 817.809554010357"
## [1] "200 Devianza: 408.010947736697"
## [1] "300 Devianza: 289.951542494061"
## [1] "400 Devianza: 227.805737974779"
## [1] "500 Devianza: 190.43408903327"
## [1] "600 Devianza: 165.487702748531"
## [1] "700 Devianza: 147.301091651991"
## [1] "800 Devianza: 133.221066964653"
## [1] "900 Devianza: 121.903186824327"
## [1] "1000 Devianza: 112.560175747607"
## [1] "1100 Devianza: 104.688785448699"
## [1] "1200 Devianza: 97.9483674585563"
## [1] "1300 Devianza: 92.0984398108757"
## [1] "1400 Devianza: 86.9631199039947"
## [1] "1500 Devianza: 82.4103777725155"
## [1] "1600 Devianza: 78.3393471851082"
## [1] "1700 Devianza: 74.6718258066508"
## [1] "1800 Devianza: 71.3463032980959"
## [1] "1900 Devianza: 68.3137316150628"
x_pr_s <- scale(x_pr, center = medias, scale = sd)
probas <- pred_multinom(x_pr_s, iteraciones[2000,])
clase <- apply(probas, 1, which.max)
table(clase - 1, y_pr )
##    y_pr
##       0   1   2   3   4   5   6   7   8   9
##   0 347   0   4   1   3   3   1   1   7   0
##   1   0 252   0   0   4   0   0   1   0   1
##   2   2   1 168   4   7   1   7   2   5   0
##   3   2   5   5 148   2   6   0   2   1   0
##   4   4   0   5   1 168   2   2   5   2   3
##   5   1   0   2   8   3 139   3   0   6   1
##   6   0   3   2   1   3   2 156   0   2   0
##   7   1   1   4   1   3   0   0 133   2   3
##   8   1   1   8   1   3   5   1   0 136   3
##   9   1   1   0   1   4   2   0   3   5 166
1 - mean(clase-1 != y_pr)
## [1] 0.9033383

Tarea 4

Ver tareas/tarea_4.Rmd.