Clase 13 Métodos basados en árboles: boosting

Boosting también utiliza la idea de un “ensamble” de árboles. La diferencia grande con bagging y bosques aleatorios en que la sucesión de árboles de boosting se ‘adapta’ al comportamiento del predictor a lo largo de las iteraciones, haciendo reponderaciones de los datos de entrenamiento para que el algoritmo se concentre en las predicciones más pobres. Boosting generalmente funciona bien con árboles chicos (cada uno con sesgo alto), mientras que bosques aleatorios funciona con árboles grandes (sesgo bajo).

En boosting usamos muchos árboles chicos adaptados secuencialmente. La disminución del sesgo proviene de usar distintos árboles que se encargan de adaptar el predictor a distintas partes del conjunto de entrenamiento. El control de varianza se logra con tasas de aprendizaje y tamaño de árboles, como veremos más adelante.
En bosques aleatorios usamos muchos árboles grandes, cada uno con una muestra de entrenamiento perturbada (bootstrap). El control de varianza se logra promediando sobre esas muestras bootstrap de entrenamiento.

Igual que bosques aleatorios, boosting es también un método que generalmente tiene alto poder predictivo.

13.1 Forward stagewise additive modeling (FSAM)

Aunque existen versiones de boosting (Adaboost) desde los 90s, una buena manera de entender los algoritmos es mediante un proceso general de modelado por estapas (FSAM).

13.2 Discusión

Consideramos primero un problema de regresión, que queremos atacar con un predictor de la forma \[f(x) = \sum_{k=1}^m \beta_k b_k(x),\] donde los \(b_k\) son árboles. Podemos absorber el coeficiente \(\beta_k\) dentro del árbol \(b_k(x)\), y escribimos

\[f(x) = \sum_{k=1}^m T_k(x),\]

Para ajustar este tipo de modelos, buscamos minimizar la pérdida de entrenamiento:

\[\begin{equation} \min \sum_{i=1}^N L(y^{(i)}, \sum_{k=1}^M T_k(x^{(i)})) \end{equation}\]

Este puede ser un problema difícil, dependiendo de la familia que usemos para los árboles \(T_k\), y sería difícil resolver por fuerza bruta. Para resolver este problema, podemos intentar una heurística secuencial o por etapas:

Si tenemos \[f_{m-1}(x) = \sum_{k=1}^{m-1} T_k(x),\]

intentamos resolver el problema (añadir un término adicional)

\[\begin{equation} \min_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)})) \end{equation}\]

Por ejemplo, para pérdida cuadrática (en regresión), buscamos resolver

\[\begin{equation} \min_{T} \sum_{i=1}^N (y^{(i)} - f_{m-1}(x^{(i)}) - T(x^{(i)}))^2 \end{equation}\]

Si ponemos \[ r_{m-1}^{(i)} = y^{(i)} - f_{m-1}(x^{(i)}),\] que es el error para el caso \(i\) bajo el modelo \(f_{m-1}\), entonces reescribimos el problema anterior como \[\begin{equation} \min_{T} \sum_{i=1}^N ( r_{m-1}^{(i)} - T(x^{(i)}))^2 \end{equation}\]

Este problema consiste en ajustar un árbol a los residuales o errores del paso anterior. Otra manera de decir esto es que añadimos un término adicional que intenta corregir los que el modelo anterior no pudo predecir bien. La idea es repetir este proceso para ir reduciendo los residuales, agregando un árbol a la vez.

La primera idea central de boosting es concentrarnos, en el siguiente paso, en los datos donde tengamos errores, e intentar corregir añadiendo un término adicional al modelo.

13.3 Algoritmo FSAM

Esta idea es la base del siguiente algoritmo:

Algoritmo FSAM (forward stagewise additive modeling)

Tomamos \(f_0(x)=0\)
Para \(m=1\) hasta \(M\),

Resolvemos \[T_m = argmin_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)}))\]
Ponemos \[f_m(x) = f_{m-1}(x) + T_m(x)\]

Nuestro predictor final es \(f(x) = \sum_{m=1}^M T_(x)\).

Observaciones: Generalmente los árboles sobre los que optimizamos están restringidos a una familia relativamente chica: por ejemplo, árboles de profundidad no mayor a \(2,3,\ldots, 8\).

Este algoritmo se puede aplicar directamente para problemas de regresión, como vimos en la discusión anterior: simplemente hay que ajustar árboles a los residuales del modelo del paso anterior. Sin embargo, no está claro cómo aplicarlo cuando la función de pérdida no es mínimos cuadrados (por ejemplo, regresión logística).

Ejemplo (regresión)

Podemos hacer FSAM directamente sobre un problema de regresión.

set.seed(227818)
library(rpart)
library(tidyverse)
x <- rnorm(200, 0, 30)
y <- 2*ifelse(x < 0, 0, sqrt(x)) + rnorm(200, 0, 0.5)
dat <- data.frame(x=x, y=y)

Pondremos los árboles de cada paso en una lista. Podemos comenzar con una constante en lugar de 0.

arboles_fsam <- list()
arboles_fsam[[1]] <- rpart(y~x, data = dat, 
                           control = list(maxdepth=0))
arboles_fsam[[1]]

## n= 200 
## 
## node), split, n, deviance, yval
##       * denotes terminal node
## 
## 1) root 200 5370.398 4.675925 *

Ahora construirmos nuestra función de predicción y el paso que agrega un árbol

predecir_arboles <- function(arboles_fsam, x){
  preds <- lapply(arboles_fsam, function(arbol){
    predict(arbol, data.frame(x=x))
  })
  reduce(preds, `+`)
}
agregar_arbol <- function(arboles_fsam, dat, plot=TRUE){
  n <- length(arboles_fsam)
  preds <- predecir_arboles(arboles_fsam, x=dat$x)
  dat$res <- y - preds
  arboles_fsam[[n+1]] <- rpart(res ~ x, data = dat, 
                           control = list(maxdepth = 1))
  dat$preds_nuevo <- predict(arboles_fsam[[n+1]])
  dat$preds <- predecir_arboles(arboles_fsam, x=dat$x)
  g_res <- ggplot(dat, aes(x = x)) + geom_line(aes(y=preds_nuevo)) +
    geom_point(aes(y=res)) + labs(title = 'Residuales') + ylim(c(-10,10))
  g_agregado <- ggplot(dat, aes(x=x)) + geom_line(aes(y=preds), col = 'red',
                                                  size=1.1) +
    geom_point(aes(y=y)) + labs(title ='Ajuste')
  if(plot){
    print(g_res)
    print(g_agregado)
  }
  arboles_fsam
}

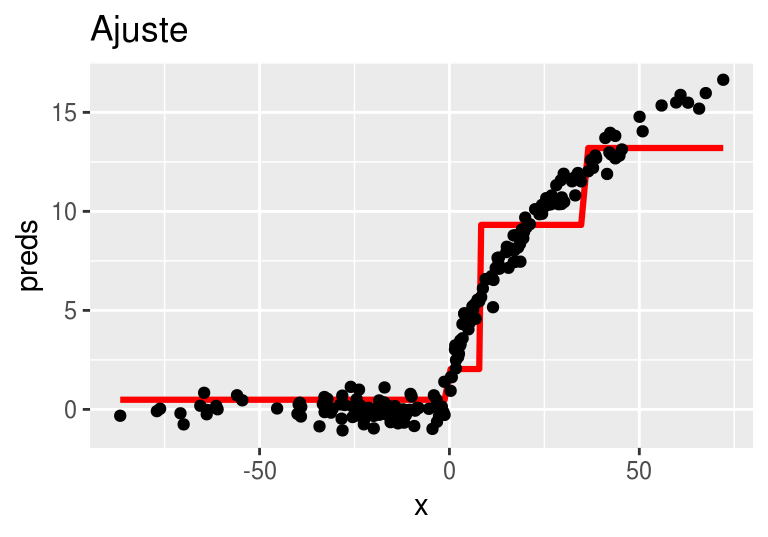
Ahora construiremos el primer árbol. Usaremos ‘troncos’ (stumps), árboles con un solo corte: Los primeros residuales son simplemente las \(y\)’s observadas

arboles_fsam <- agregar_arbol(arboles_fsam, dat)

## Warning: Removed 8 rows containing missing values (geom_point).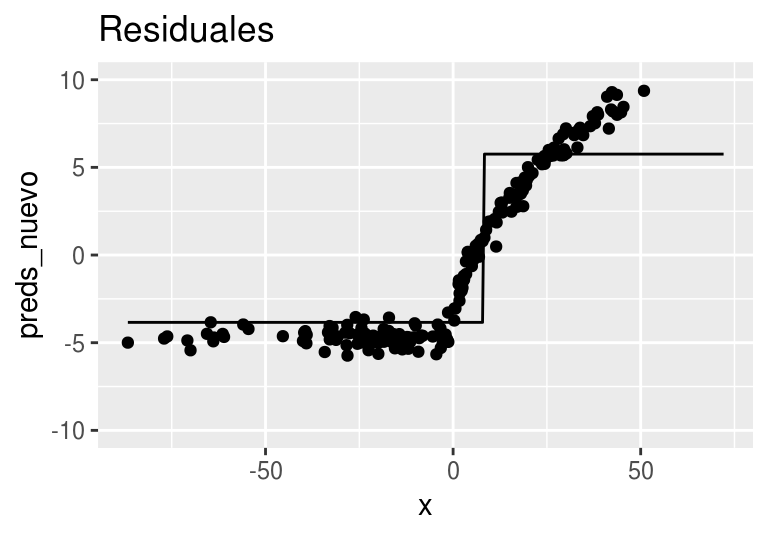

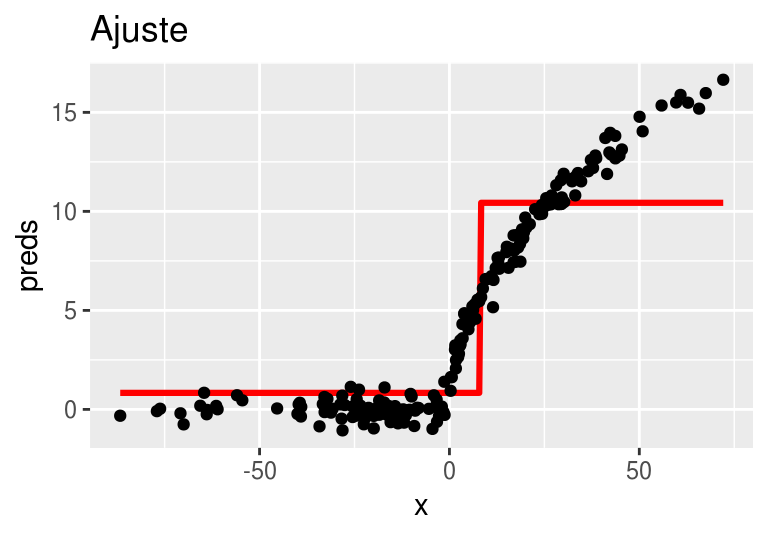
Ajustamos un árbol de regresión a los residuales:

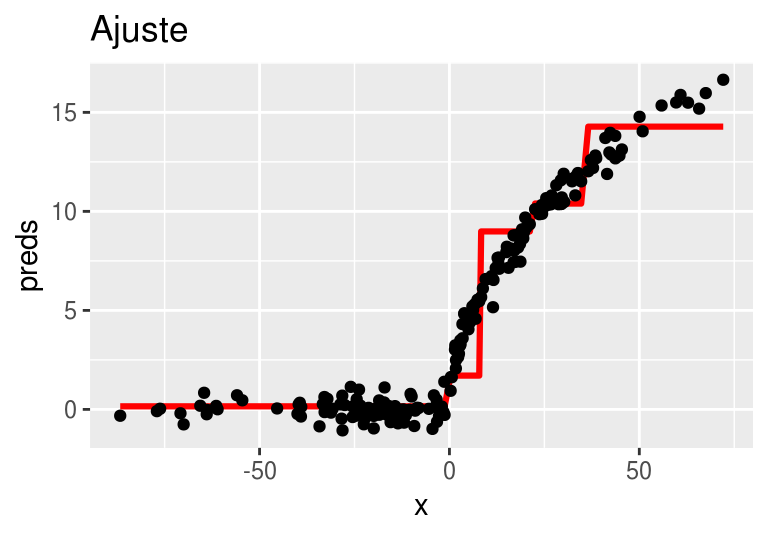
arboles_fsam <- agregar_arbol(arboles_fsam, dat)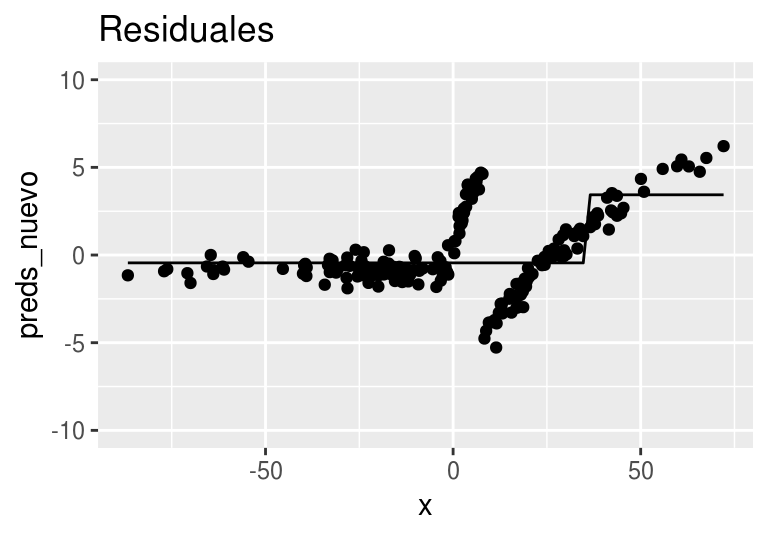

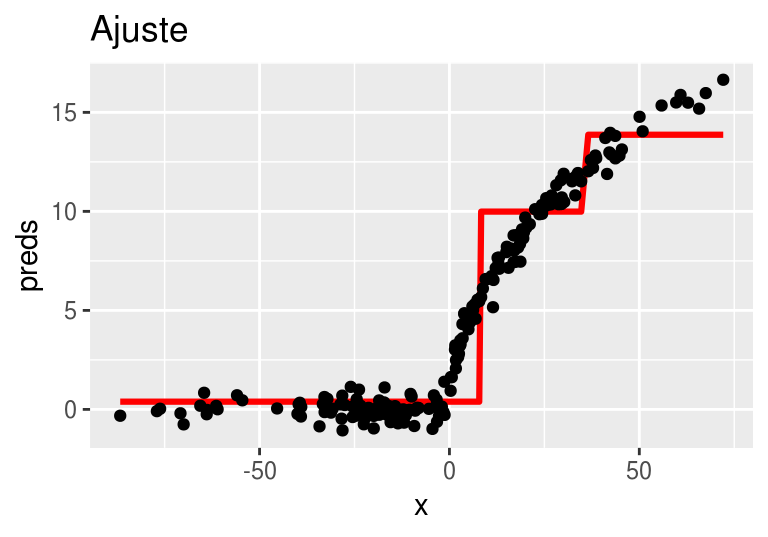
arboles_fsam <- agregar_arbol(arboles_fsam, dat)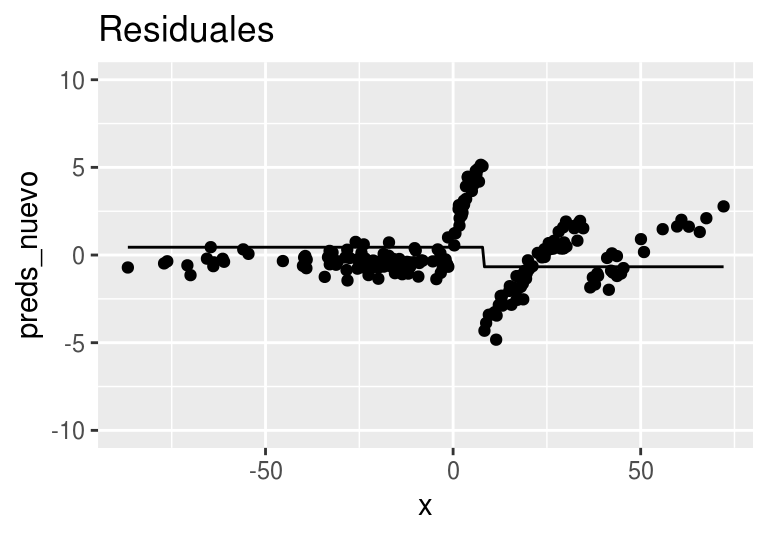

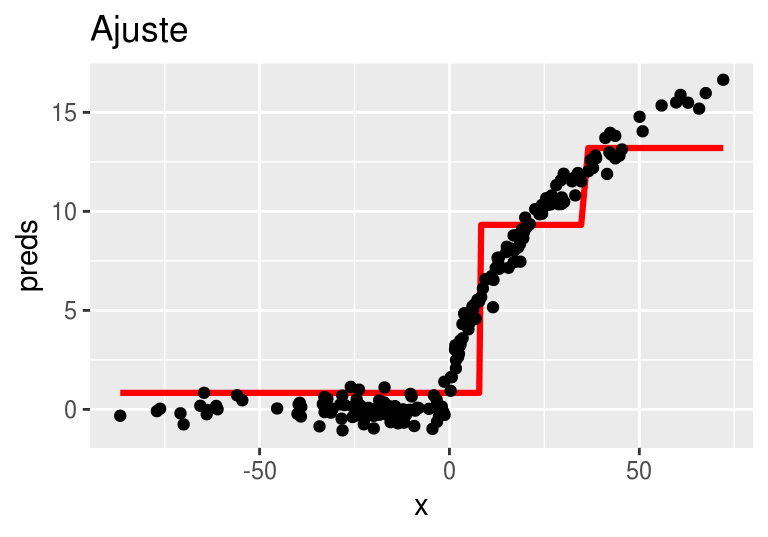
arboles_fsam <- agregar_arbol(arboles_fsam, dat)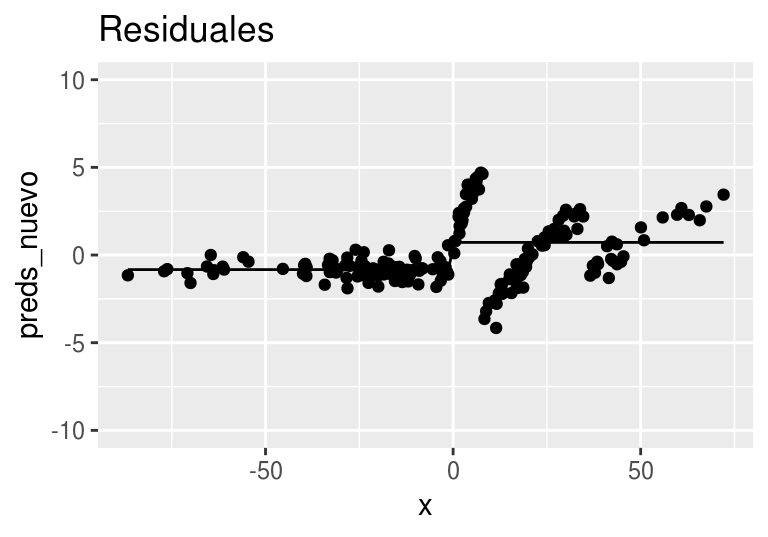

arboles_fsam <- agregar_arbol(arboles_fsam, dat)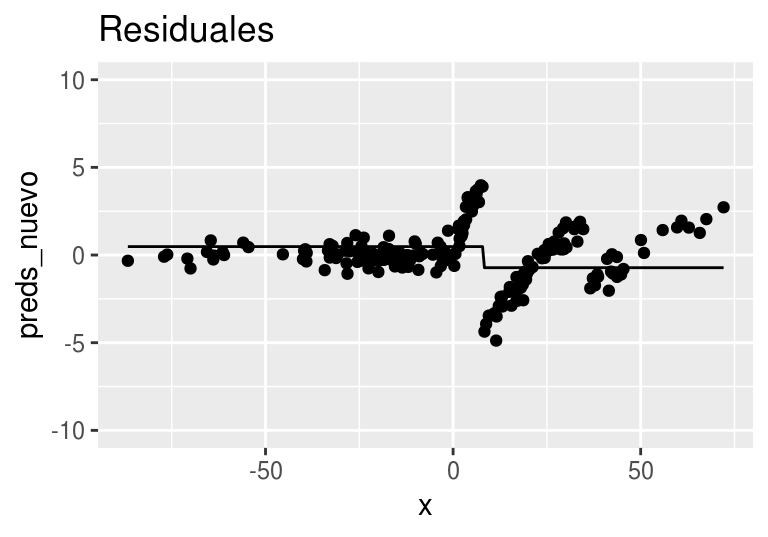

arboles_fsam <- agregar_arbol(arboles_fsam, dat)

Después de 20 iteraciones obtenemos:

for(j in 1:19){
arboles_fsam <- agregar_arbol(arboles_fsam, dat, plot = FALSE)
}
arboles_fsam <- agregar_arbol(arboles_fsam, dat)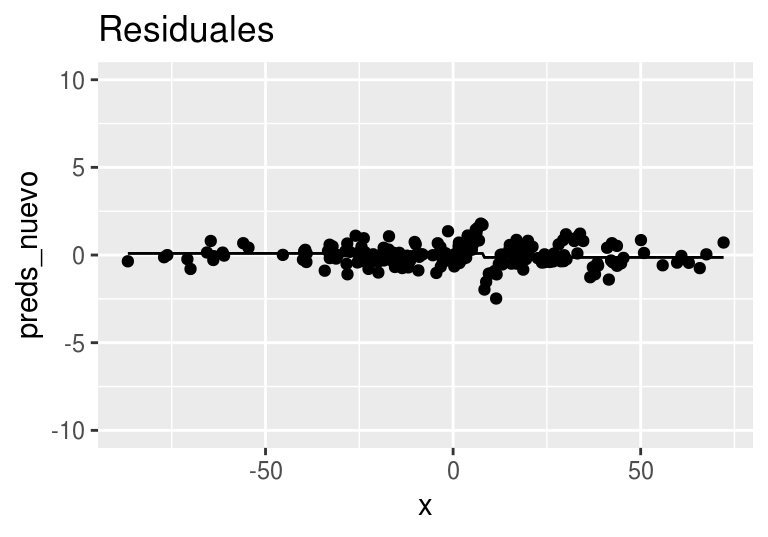

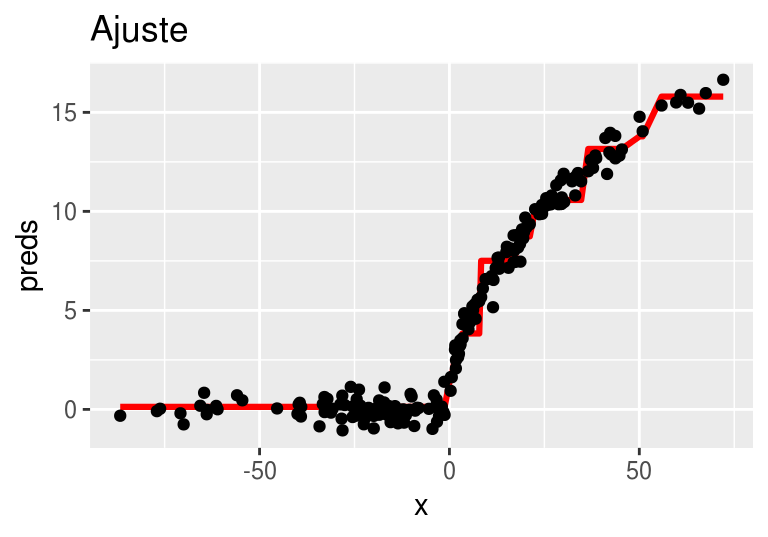
13.4 FSAM para clasificación binaria.

Para problemas de clasificación, no tiene mucho sentido trabajar con un modelo aditivo sobre las probabilidades:

\[p(x) = \sum_{k=1}^m T_k(x),\]

Así que hacemos lo mismo que en regresión logística. Ponemos

\[f(x) = \sum_{k=1}^m T_k(x),\]

y entonces las probabilidades son \[p(x) = h(f(x)),\]

donde \(h(z)=1/(1+e^{-z})\) es la función logística. La optimización de la etapa \(m\) según fsam es

\[\begin{equation} T = argmin_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)})) \tag{13.1} \end{equation}\]

y queremos usar la devianza como función de pérdida. Por razones de comparación (con nuestro libro de texto y con el algoritmo Adaboost que mencionaremos más adelante), escogemos usar \[y \in \{1,-1\}\]

en lugar de nuestro tradicional \(y \in \{1,0\}\). En ese caso, la devianza binomial se ve como

\[L(y, z) = -\left [ (y+1)\log h(z) - (y-1)\log(1-h(z))\right ],\] que a su vez se puede escribir como (demostrar):

\[L(y,z) = 2\log(1+e^{-yz})\] Ahora consideremos cómo se ve nuestro problema de optimización:

\[T = argmin_{T} 2\sum_{i=1}^N \log (1+ e^{-y^{(i)}(f_{m-1}(x^{(i)}) + T(x^{(i)})})\]

Nótese que sólo optimizamos con respecto a \(T\), así que podemos escribir

\[T = argmin_{T} 2\sum_{i=1}^N \log (1+ d_{m,i}e^{- y^{(i)}T(x^{(i)})})\]

Y vemos que el problema es más difícil que en regresión. No podemos usar un ajuste de árbol usual de regresión o clasificación, como hicimos en regresión. No está claro, por ejemplo, cuál debería ser el residual que tenemos que ajustar (aunque parece un problema donde los casos de entrenamiento están ponderados por \(d_{m,i}\)). Una solución para resolver aproximadamente este problema de minimización, es gradient boosting.

13.5 Gradient boosting

La idea de gradient boosting es replicar la idea del residual en regresión, y usar árboles de regresión para resolver (13.1).

Gradient boosting es una técnica general para funciones de pérdida generales.Regresamos entonces a nuestro problema original

\[(\beta_m, b_m) = argmin_{T} \sum_{i=1}^N L(y^{(i)}, f_{m-1}(x^{(i)}) + T(x^{(i)}))\]

La pregunta es: ¿hacia dónde tenemos qué mover la predicción de \(f_{m-1}(x^{(i)})\) sumando el término \(T(x^{(i)})\)? Consideremos un solo término de esta suma, y denotemos \(z_i = T(x^{(i)})\). Queremos agregar una cantidad \(z_i\) tal que el valor de la pérdida \[L(y, f_{m-1}(x^{(i)})+z_i)\] se reduzca. Entonces sabemos que podemos mover la z en la dirección opuesta al gradiente

\[z_i = -\gamma \frac{\partial L}{\partial z}(y^{(i)}, f_{m-1}(x^{(i)}))\]

Sin embargo, necesitamos que las \(z_i\) estén generadas por una función \(T(x)\) que se pueda evaluar en toda \(x\). Quisiéramos que \[T(x^{(i)})\approx -\gamma \frac{\partial L}{\partial z}(y^{(i)}, f_{m-1}(x^{(i)}))\] Para tener esta aproximación, podemos poner \[g_{i,m} = -\frac{\partial L}{\partial z}(y^{(i)}, f_{m-1}(x^{(i)}))\] e intentar resolver \[\begin{equation} \min_T \sum_{i=1}^n (g_{i,m} - T(x^{(i)}))^2, \tag{13.2} \end{equation}\]

es decir, intentamos replicar los gradientes lo más que sea posible. Este problema lo podemos resolver con un árbol usual de regresión. Finalmente, podríamos escoger \(\nu\) (tamaño de paso) suficientemente chica y ponemos \[f_m(x) = f_{m-1}(x)+\nu T(x).\]

Podemos hacer un refinamiento adicional que consiste en encontrar los cortes del árbol \(T\) según (13.2), pero optimizando por separado los valores que T(x) toma en cada una de las regiones encontradas.

13.6 Algoritmo de gradient boosting

Gradient boosting (versión simple)

Inicializar con \(f_0(x) =\gamma\)
Para \(m=0,1,\ldots, M\),

Para \(i=1,\ldots, n\), calculamos el residual \[r_{i,m}=-\frac{\partial L}{\partial z}(y^{(i)}, f_{m-1}(x^{(i)}))\]
Ajustamos un árbol de regresión a la respuesta \(r_{1,m},r_{2,m},\ldots, r_{n,m}\). Supongamos que tiene regiones \(R_{j,m}\).
Resolvemos (optimizamos directamente el valor que toma el árbol en cada región - este es un problema univariado, más fácil de resolver) \[\gamma_{j,m} = argmin_\gamma \sum_{x^{(i)}\in R_{j,m}} L(y^{(i)},f_{m-1}(x^{i})+\gamma )\] para cada región \(R_{j,m}\) del árbol del inciso anterior.
Actualizamos \[f_m (x) = f_{m-1}(x) + \sum_j \gamma_{j,m} I(x\in R_{j,m})\]

El predictor final es \(f_M(x)\).

13.7 Funciones de pérdida

Para aplicar gradient boosting, tenemos primero que poder calcular el gradiente de la función de pérdida. Algunos ejemplos populares son:

Pérdida cuadrática: \(L(y,f(x))=(y-f(x))^2\), \(\frac{\partial L}{\partial z} = -2(y-f(x))\).
Pérdida absoluta (más robusta a atípicos que la cuadrática) \(L(y,f(x))=|y-f(x)|\), \(\frac{\partial L}{\partial z} = signo(y-f(x))\).
Devianza binomial \(L(y, f(x))\) = -(1+e^{-yf(x)}), \(y\in\{-1,1\}\), \(\frac{\partial L}{\partial z} = I(y=1) - h(f(x))\).
Adaboost, pérdida exponencial (para clasificación) \(L(y,z) = e^{-yf(x)}\), \(y\in\{-1,1\}\), \(\frac{\partial L}{\partial z} = -ye^{-yf(x)}\).

13.7.1 Discusión: adaboost (opcional)

Adaboost es uno de los algoritmos originales para boosting, y no es necesario usar gradient boosting para aplicarlo. La razón es que los árboles de clasificación \(T(x)\) toman valores \(T(x)\in \{-1,1\}\), y el paso de optimización (13.1) de cada árbol queda

\[T = argmin_{T} \sum_{i=1}^N e^{-y^{(i)}f_{m-1}(x^{(i)})} e^{-y^{(i)}T(x^{(i)})} \] \[T = argmin_{T} \sum_{i=1}^N d_{m,i} e^{-y^{(i)}T(x^{(i)})} \] De modo que la función objetivo toma dos valores: Si \(T(x^{i})\) clasifica correctamente, entonces \(e^{-y^{(i)}T(x^{(i)})}=e^{-1}\), y si clasifica incorrectamente \(e^{-y^{(i)}T(x^{(i)})}=e^{1}\). Podemos entonces encontrar el árbol \(T\) construyendo un árbol usual pero con datos ponderados por \(d_{m,i}\), donde buscamos maximizar la tasa de clasificación correcta (puedes ver más en nuestro libro de texto, o en (Hastie, Tibshirani, and Friedman 2017).

¿Cuáles son las consecuencias de usar la pérdida exponencial? Una es que perdemos la conexión con los modelos logísticos e interpretación de probabilidad que tenemos cuando usamos la devianza. Sin embargo, son similares: compara cómo se ve la devianza (como la formulamos arriba, con \(y\in\{-1,1\}\)) con la pérdida exponencial.

Ejemplo

Podemos usar el paquete de R gbm para hacer gradient boosting. Para el caso de precios de casas de la sección anterior (un problema de regresión). Para ver un ejemplo distinto, utilizaremos la pérdida absoluta en lugar de pérdida cuadrática:

Fijaremos el número de árboles en 200, de profundidad 3, usando 75% de la muestra para entrenar y el restante para validación:

library(gbm)
entrena <- read_rds('datos/ameshousing-entrena-procesado.rds')
set.seed(23411)

ajustar_boost <- function(entrena, ...){
  mod_boosting <- gbm(log(vSalePrice) ~.,  data = entrena,
                distribution = 'laplace',
                n.trees = 200, 
                interaction.depth = 3,
                shrinkage = 1, # tasa de aprendizaje
                bag.fraction = 1,
                train.fraction = 0.75)
  mod_boosting
}

house_boosting <- ajustar_boost(entrena)
dat_entrenamiento <- data_frame(entrena = house_boosting$train.error,
                                valida = house_boosting$valid.error,
                                n_arbol = 1:length(house_boosting$train.error)) %>%
                      gather(tipo, valor, -n_arbol)
print(house_boosting)

## gbm(formula = log(vSalePrice) ~ ., distribution = "laplace", 
##     data = entrena, n.trees = 200, interaction.depth = 3, shrinkage = 1, 
##     bag.fraction = 1, train.fraction = 0.75)
## A gradient boosted model with laplace loss function.
## 200 iterations were performed.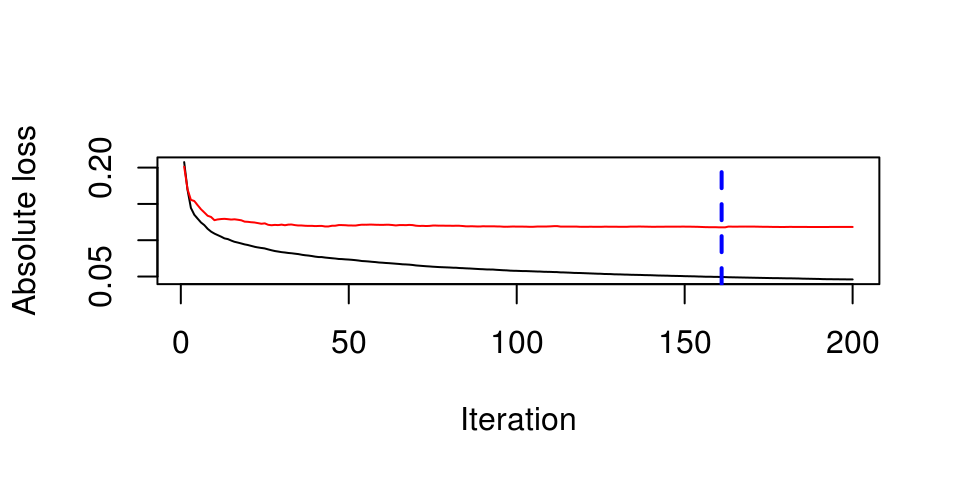

## The best test-set iteration was 161.
## There were 79 predictors of which 63 had non-zero influence.

ggplot(dat_entrenamiento, aes(x=n_arbol, y=valor, colour=tipo, group=tipo)) +
  geom_line()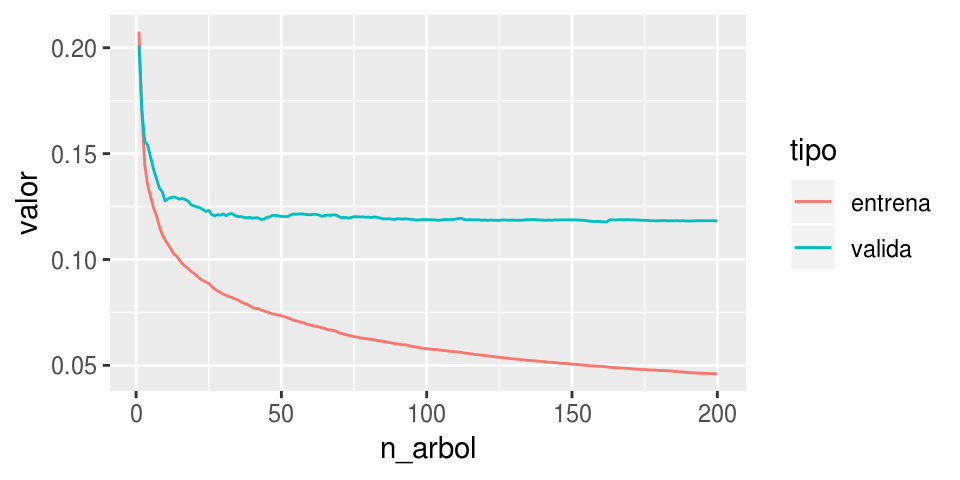

Que se puede graficar también así:

gbm.perf(house_boosting)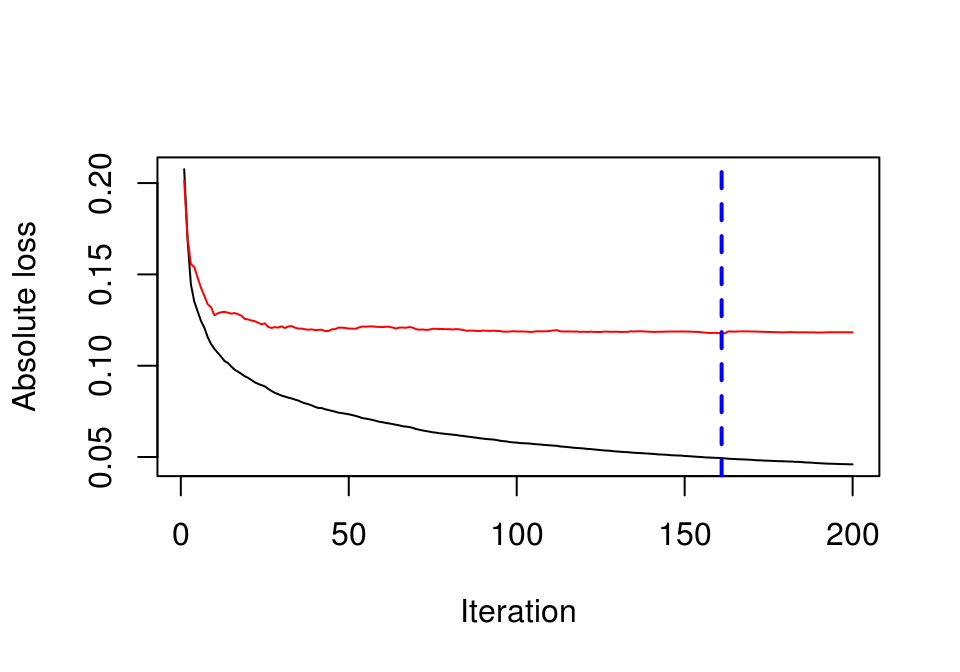

## [1] 161

Como vemos, tenemos que afinar los parámetros del algoritmo.

13.8 Modificaciones de Gradient Boosting

Hay algunas adiciones al algoritmo de gradient boosting que podemos usar para mejorar el desempeño. Los dos métodos que comunmente se usan son encogimiento (shrinkage), que es una especie de tasa de aprendizaje, y submuestreo, donde construimos cada árbol adicional usando una submuestra de la muestra de entrenamiento.

Ambas podemos verlas como técnicas de regularización, que limitan sobreajuste producido por el algoritmo agresivo de boosting.

13.8.1 Tasa de aprendizaje (shrinkage)

Funciona bien modificar el algoritmo usando una tasa de aprendizae \(0<\nu<1\): \[f_m(x) = f_{m-1}(x) + \nu \sum_j \gamma_{j,m} I(x\in R_{j,m})\]

Este parámetro sirve como una manera de evitar sobreajuste rápido cuando construimos los predictores. Si este número es muy alto, podemos sobreajustar rápidamente con pocos árboles, y terminar con predictor de varianza alta. Si este número es muy bajo, puede ser que necesitemos demasiadas iteraciones para llegar a buen desempeño.

Igualmente se prueba con varios valores de \(0<\nu<1\) (típicamente \(\nu<0.1\)) para mejorar el desempeño en validación. Nota: cuando hacemos \(\nu\) más chica, es necesario hacer \(M\) más grande (correr más árboles) para obtener desempeño óptimo.

Veamos que efecto tiene en nuestro ejemplo:

modelos_dat <- data_frame(n_modelo = 1:4, shrinkage = c(0.02, 0.05, 0.25, 0.5))
modelos_dat <- modelos_dat %>% 
  mutate(modelo = map(shrinkage, boost)) %>%
  mutate(eval = map(modelo, eval_modelo))
modelos_dat

## # A tibble: 4 x 4
##   n_modelo shrinkage modelo    eval                
##      <int>     <dbl> <list>    <list>              
## 1        1      0.02 <S3: gbm> <tibble [1,000 × 3]>
## 2        2      0.05 <S3: gbm> <tibble [1,000 × 3]>
## 3        3      0.25 <S3: gbm> <tibble [1,000 × 3]>
## 4        4      0.5  <S3: gbm> <tibble [1,000 × 3]>

graf_eval <- modelos_dat %>% select(shrinkage, eval) %>% unnest
graf_eval

## # A tibble: 4,000 x 4
##    shrinkage n_arbol tipo    valor
##        <dbl>   <int> <chr>   <dbl>
##  1      0.02       1 entrena 0.309
##  2      0.02       2 entrena 0.305
##  3      0.02       3 entrena 0.301
##  4      0.02       4 entrena 0.297
##  5      0.02       5 entrena 0.294
##  6      0.02       6 entrena 0.290
##  7      0.02       7 entrena 0.287
##  8      0.02       8 entrena 0.283
##  9      0.02       9 entrena 0.280
## 10      0.02      10 entrena 0.277
## # ... with 3,990 more rows

ggplot(filter(graf_eval), 
       aes(x = n_arbol, y= valor, 
           colour=factor(shrinkage), group = shrinkage)) + 
    geom_line() +
  facet_wrap(~tipo)

Obsérvese que podemos obtener un mejor resultado de validación afinando la tasa de aprendizaje. Cuando es muy grande, el modelo rápidamente sobreajusta cuando agregamos árboles. Si la tasa es demasiado chica, podos tardar mucho en llegar a un predictor de buen desempeño.

13.8.2 Submuestreo (bag.fraction)

Funciona bien construir cada uno de los árboles con submuestras de la muestra de entrenamiento, como una manera adicional de reducir varianza al construir nuestro predictor (esta idea es parecida a la de los bosques aleatorios, aquí igualmente perturbamos la muestra de entrenamiento en cada paso para evitar sobreajuste). Adicionalmente, este proceso acelera considerablemente las iteraciones de boosting, y en algunos casos sin penalización en desempeño.

En boosting generalmente se toman submuestras (una fracción de alrededor de 0.5 de la muestra de entrenamiento, pero puede ser más chica para conjuntos grandes de entrenamiento) sin reemplazo.

Este parámetro también puede ser afinado con muestra de validación o validación cruzada.

boost <- ajustar_boost(entrena)
modelos_dat <- data_frame(n_modelo = 1:3, 
                          bag.fraction = c(0.25, 0.5, 1),
                          shrinkage = 0.25)
modelos_dat <- modelos_dat %>% 
  mutate(modelo = pmap(., boost)) %>%
  mutate(eval = map(modelo, eval_modelo))
modelos_dat

## # A tibble: 3 x 5
##   n_modelo bag.fraction shrinkage modelo    eval                
##      <int>        <dbl>     <dbl> <list>    <list>              
## 1        1         0.25      0.25 <S3: gbm> <tibble [1,000 × 3]>
## 2        2         0.5       0.25 <S3: gbm> <tibble [1,000 × 3]>
## 3        3         1         0.25 <S3: gbm> <tibble [1,000 × 3]>

graf_eval <- modelos_dat %>% select(bag.fraction, eval) %>% unnest
graf_eval

## # A tibble: 3,000 x 4
##    bag.fraction n_arbol tipo    valor
##           <dbl>   <int> <chr>   <dbl>
##  1         0.25       1 entrena 0.269
##  2         0.25       2 entrena 0.232
##  3         0.25       3 entrena 0.211
##  4         0.25       4 entrena 0.194
##  5         0.25       5 entrena 0.179
##  6         0.25       6 entrena 0.170
##  7         0.25       7 entrena 0.162
##  8         0.25       8 entrena 0.152
##  9         0.25       9 entrena 0.147
## 10         0.25      10 entrena 0.142
## # ... with 2,990 more rows

ggplot((graf_eval), aes(x = n_arbol, y= valor, colour=factor(bag.fraction), group =
                        bag.fraction)) + geom_line() +
  facet_wrap(~tipo, ncol = 1)

En este ejemplo, podemos reducir el tiempo de ajuste usando una fracción de submuestro de 0.5, con quizá algunas mejoras en desempeño.

Ahora veamos los dos parámetros actuando en conjunto:

modelos_dat <- list(bag.fraction = c(0.1, 0.25, 0.5, 1),
                          shrinkage = c(0.01, 0.1, 0.25, 0.5)) %>% expand.grid
modelos_dat <- modelos_dat %>% 
  mutate(modelo = pmap(., boost)) %>%
  mutate(eval = map(modelo, eval_modelo))
graf_eval <- modelos_dat %>% select(shrinkage, bag.fraction, eval) %>% unnest
head(graf_eval)

##   shrinkage bag.fraction n_arbol    tipo     valor
## 1      0.01          0.1       1 entrena 0.3108616
## 2      0.01          0.1       2 entrena 0.3087372
## 3      0.01          0.1       3 entrena 0.3065518
## 4      0.01          0.1       4 entrena 0.3047564
## 5      0.01          0.1       5 entrena 0.3027629
## 6      0.01          0.1       6 entrena 0.3010770

ggplot(filter(graf_eval, tipo =='valida'), aes(x = n_arbol, y= valor, colour=factor(bag.fraction), group =
                        bag.fraction)) + geom_line() +
  facet_wrap(~shrinkage)

Bag fraction demasiado chico no funciona bien, especialmente si la tasa de aprendizaje es alta (¿Por qué?). Filtremos para ver con detalle el resto de los datos:

ggplot(filter(graf_eval, tipo =='valida', bag.fraction>0.1), aes(x = n_arbol, y= valor, colour=factor(bag.fraction), group =
                        bag.fraction)) + geom_line() +
  facet_wrap(~shrinkage) + scale_y_log10()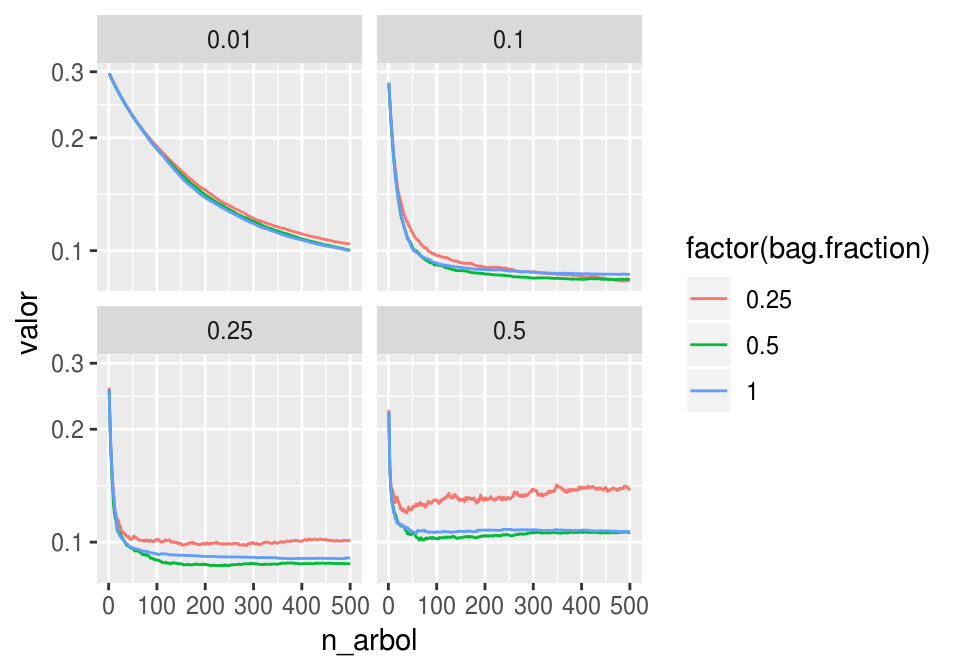

Y parece ser que para este número de iteraciones, una tasa de aprendizaje de 0.1 junto con un bag fraction de 0.5 funciona bien:

graf_eval %>% filter(tipo=='valida') %>%
  group_by(shrinkage, bag.fraction) %>%
  summarise(valor = min(valor)) %>%
   arrange(valor) %>% head(10)

## # A tibble: 10 x 3
## # Groups:   shrinkage [4]
##    shrinkage bag.fraction  valor
##        <dbl>        <dbl>  <dbl>
##  1      0.1          0.25 0.0830
##  2      0.1          0.5  0.0837
##  3      0.1          1    0.0864
##  4      0.25         0.5  0.0865
##  5      0.25         1    0.0903
##  6      0.1          0.1  0.0964
##  7      0.25         0.25 0.0979
##  8      0.01         1    0.100 
##  9      0.01         0.5  0.100 
## 10      0.5          0.5  0.101

13.8.3 Número de árboles M

Se monitorea el error sobre una muestra de validación cuando agregamos cada árboles. Escogemos el número de árboles de manera que minimize el error de validación. Demasiados árboles pueden producir sobreajuste. Ver el ejemplo de arriba.

13.8.4 Tamaño de árboles

Los árboles se construyen de tamaño fijo \(J\), donde \(J\) es el número de cortes. Usualmente \(J=1,2,\ldots, 10\), y es un parámetro que hay que elegir. \(J\) más grande permite interacciones de orden más alto entre las variables de entrada. Se intenta con varias \(J\) y \(M\) para minimizar el error de validación.

13.8.5 Controlar número de casos para cortes

Igual que en bosques aleatorios, podemos establecer mínimos de muestra en nodos terminales, o mínimo de casos necesarios para hacer un corte.

Ejemplo

modelos_dat <- list(bag.fraction = c( 0.25, 0.5, 1),
                          shrinkage = c(0.01, 0.1, 0.25, 0.5),
                    depth = c(1,5,10,12)) %>% expand.grid
modelos_dat <- modelos_dat %>% 
  mutate(modelo = pmap(., boost)) %>%
  mutate(eval = map(modelo, eval_modelo))
graf_eval <- modelos_dat %>% select(shrinkage, bag.fraction, depth, eval) %>% unnest
ggplot(filter(graf_eval, tipo =='valida'), aes(x = n_arbol, y= valor,
    colour=factor(bag.fraction), group = bag.fraction)) + 
  geom_line() +
  facet_grid(depth~shrinkage) + scale_y_log10()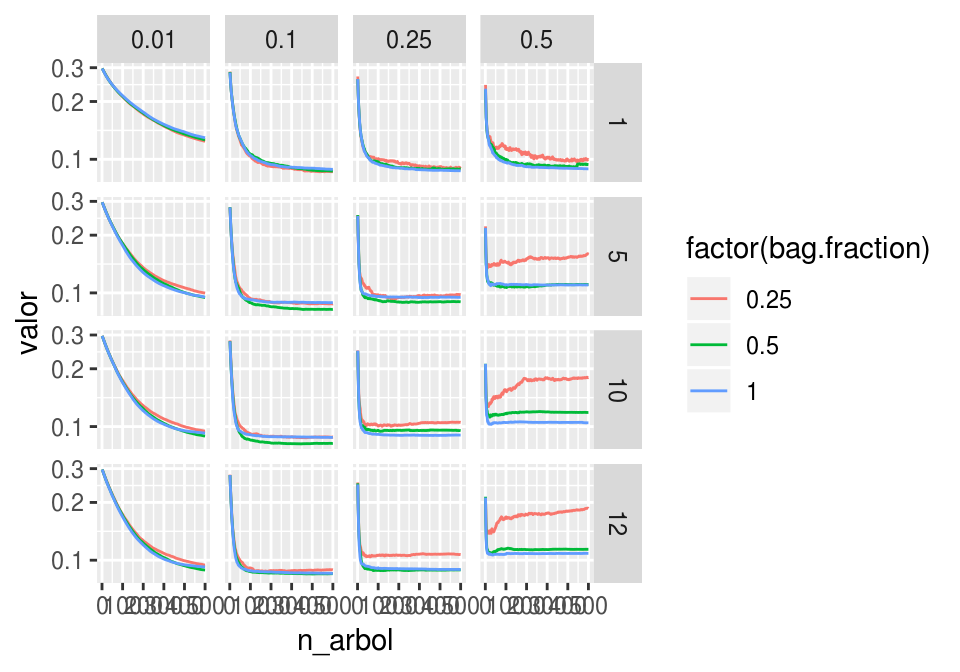

Podemos ver con más detalle donde ocurre el mejor desempeño:

ggplot(
    filter(graf_eval, tipo =='valida', shrinkage == 0.1, n_arbol > 100), aes(x = n_arbol, y= valor, colour=factor(bag.fraction), group =
                        bag.fraction)) + geom_line() +
  facet_grid(depth~shrinkage)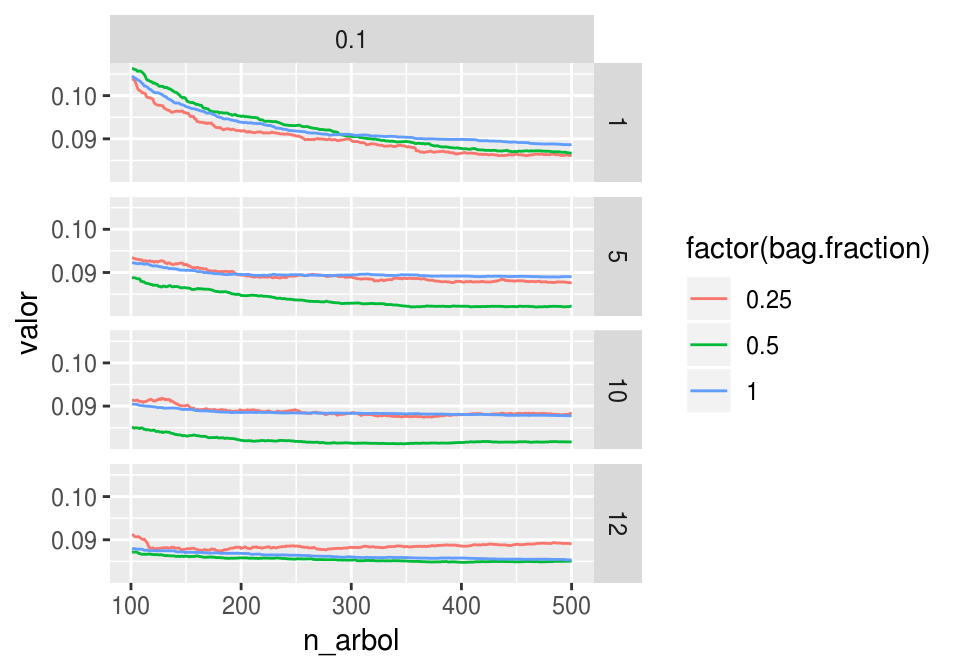

head(arrange(filter(graf_eval,tipo=='valida'), valor))

##   shrinkage bag.fraction depth n_arbol   tipo      valor
## 1       0.1          0.5    10     348 valida 0.08126603
## 2       0.1          0.5    10     342 valida 0.08128108
## 3       0.1          0.5    10     346 valida 0.08128677
## 4       0.1          0.5    10     343 valida 0.08129096
## 5       0.1          0.5    10     347 valida 0.08129531
## 6       0.1          0.5    10     341 valida 0.08129727

13.8.6 Evaluación con validación cruzada.

Para datos no muy grandes, conviene escoger modelos usando validación cruzada.

Por ejemplo,

set.seed(9983)
rm('modelos_dat')
mod_boosting <- gbm(log(vSalePrice) ~.,  data = entrena,
                distribution = 'laplace',
                n.trees = 200, 
                interaction.depth = 10,
                shrinkage = 0.1, # tasa de aprendizaje
                bag.fraction = 0.5,
                cv.folds = 10)
gbm.perf(mod_boosting)

eval_modelo_2 <- function(modelo){
   dat_eval <- data_frame(entrena = modelo$train.error,
                          valida = modelo$cv.error,
                          n_arbol = 1:length(modelo$train.error)) %>%
                      gather(tipo, valor, -n_arbol)
   dat_eval
}
dat <- eval_modelo_2(mod_boosting)
(min(mod_boosting$cv.error))
ggplot(dat, aes(x = n_arbol, y=valor, colour=tipo, group=tipo)) + geom_line()

13.9 Gráficas de dependencia parcial

La idea de dependencia parcial que veremos a continuación se puede aplicar a cualquier método de aprendizaje, y en boosting ayuda a entender el funcionamiento del predictor complejo que resulta del algoritmo. Aunque podemos evaluar el predictor en distintos valores y observar cómo se comporta, cuando tenemos varias variables de entrada este proceso no siempre tiene resultados muy claros o completos. Dependencia parcial es un intento por entender de manera más sistemática parte del funcionamiento de un modelo complejo.

13.9.1 Dependencia parcial

Supongamos que tenemos un predictor \(f(x_1,x_2)\) que depende de dos variables de entrada. Podemos considerar la función \[{f}_{1}(x_1) = E_{x_2}[f(x_1,x_2)],\] que es el promedio de \(f(x)\) fijando \(x_1\) sobre la marginal de \(x_2\). Si tenemos una muestra de entrenamiento, podríamos estimarla promediando sobre la muestra de entrenamiento

\[\bar{f}_1(x_1) = \frac{1}{n}\sum_{i=1}^n f(x_1, x_2^{(i)}),\] que consiste en fijar el valor de \(x_1\) y promediar sobre todos los valores de la muestra de entrenamiento para \(x_2\).

Ejemplo

Construimos un modelo con solamente tres variables para nuestro ejemplo anterior

mod_2 <- gbm(log(vSalePrice) ~ vGrLivArea +vNeighborhood  +
                 vOverallQual + vBsmtFinSF1,  
                data = entrena,
                distribution = 'laplace',
                n.trees = 500, 
                interaction.depth = 4,
                shrinkage = 0.1, 
                bag.fraction = 0.5,
                train.fraction = 0.75)

Podemos calcular a mano la gráfica de dependencia parcial para el tamaño de la “General Living Area”. Seleccionamos las variables:

dat_dp <- entrena %>% select(vGrLivArea, vNeighborhood, vOverallQual, vBsmtFinSF1)

Ahora consideramos el rango de la variable para establecer en dónde vamos evaluar las función de dependiencia parcial:

cuantiles <- quantile(entrena$vGrLivArea, probs= seq(0, 1, 0.1))
cuantiles

##     0%    10%    20%    30%    40%    50%    60%    70%    80%    90% 
##  334.0  912.0 1066.6 1208.0 1339.0 1464.0 1578.0 1709.3 1869.0 2158.3 
##   100% 
## 5642.0

Por ejemplo, vamos evaluar el efecto parcial cuando vGrLivArea = 912. Hacemos

dat_dp_1 <- dat_dp %>% mutate(vGrLivArea = 912) %>%
            mutate(pred = predict(mod_2, .)) %>%
            summarise(mean_pred = mean(pred))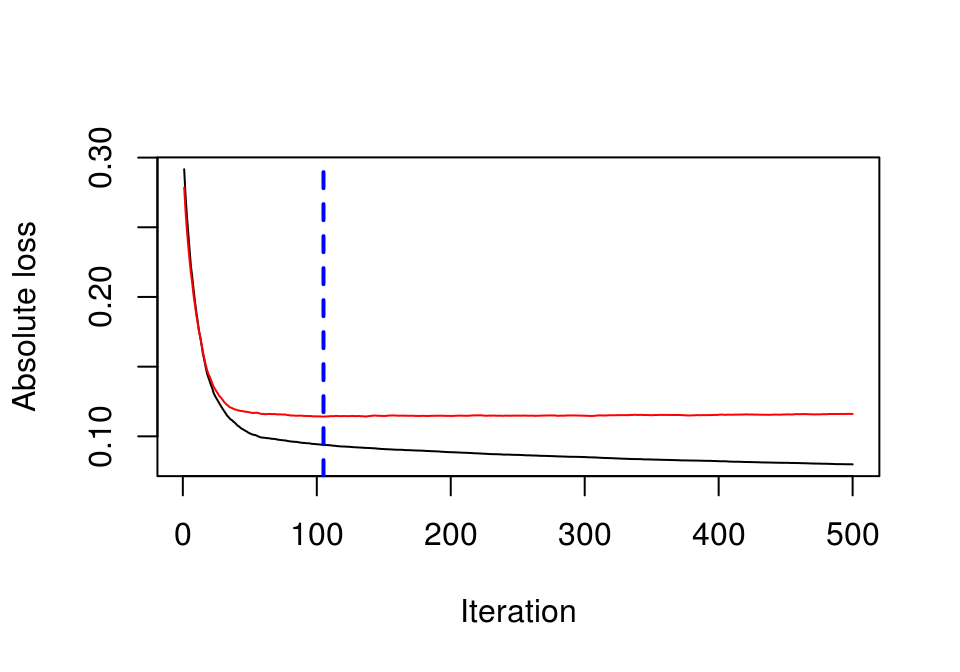

## Using 105 trees...

dat_dp_1

##   mean_pred
## 1  11.84386

Evaluamos en vGrLivArea = 1208

dat_dp_1 <- dat_dp %>% mutate(vGrLivArea = 1208) %>%
            mutate(pred = predict(mod_2, .)) %>%
            summarise(mean_pred = mean(pred))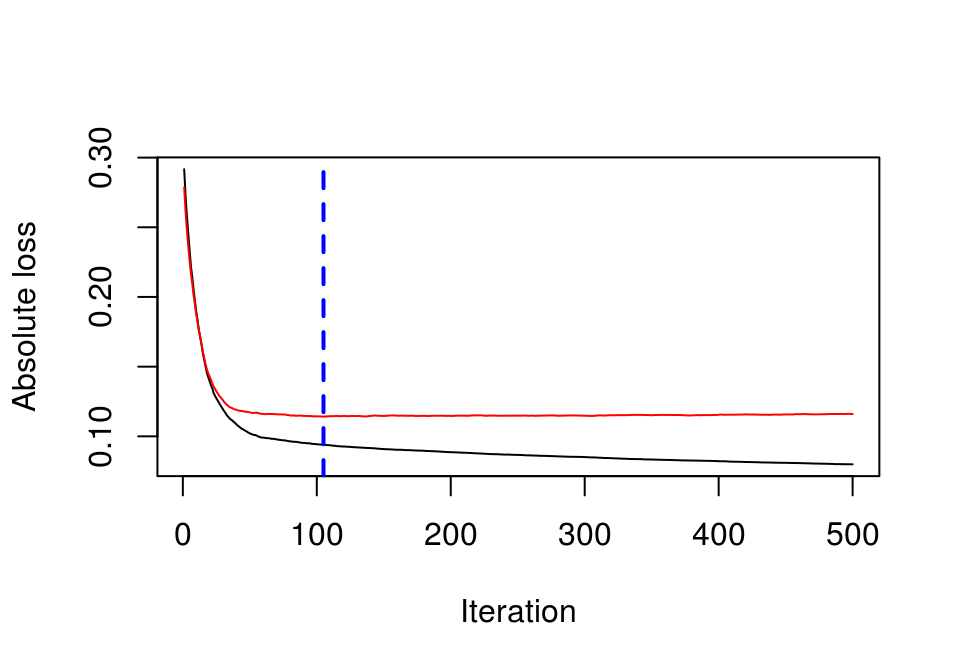

## Using 105 trees...

dat_dp_1

##   mean_pred
## 1  11.96169

(un incremento de alrededor del 10% en el precio de venta).

Hacemos todos los percentiles como sigue:

cuantiles <- quantile(entrena$vGrLivArea, probs= seq(0, 1, 0.01))

prom_parcial <- function(x, variable, df, mod){
  variable <- enquo(variable)
  variable_nom <- quo_name(variable)
  salida <- df %>% mutate(!!variable_nom := x) %>% 
    mutate(pred = predict(mod, ., n.trees = 500)) %>%
    group_by(!!variable) %>%
    summarise(f_1 = mean(pred)) 
  salida
}
dep_parcial <- map_dfr(cuantiles, 
                       ~prom_parcial(.x, vGrLivArea, entrena, mod_2))
ggplot(dep_parcial, aes(x=vGrLivArea, y = f_1)) + 
  geom_line() + geom_line() + geom_rug(sides='b')

Y transformando a las unidades originales

ggplot(dep_parcial, aes(x=vGrLivArea, y= exp(f_1))) + 
  geom_line() + geom_line() + geom_rug(sides='b')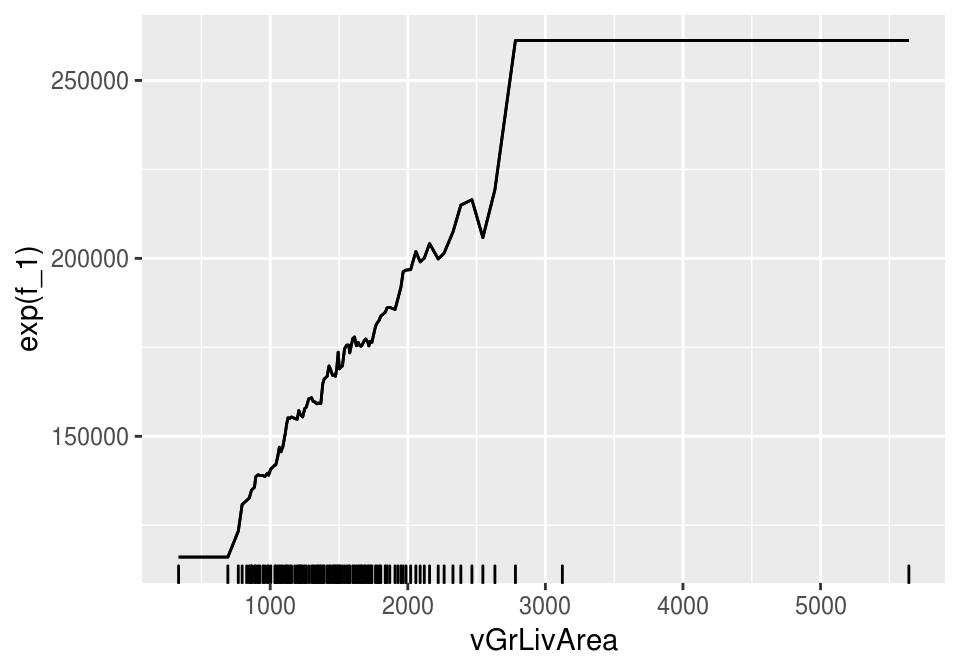

Y vemos que cuando aumenta el area de habitación, aumenta el precio. Podemos hacer esta gráfica más simple haciendo

plot(mod_2, 1) # 1 pues es vGrLivArea la primer variable

Discusión

En primer lugar, veamos qué obtenemos de la dependencia parcial cuando aplicamos al modelo lineal sin interacciones. En el caso de dos variables,

\[f_1(x_1) = E_{x_2}[f(x_1,x_2)] =E_{x_2}[a + bx_1 + cx_2)] = \mu + bx_1,\] que es equivalente al análisis marginal que hacemos en regresión lineal ( incrementos en la variable \(x_1\) con todo lo demás fijo, donde el incremento marginal de la respuesta es el coeficiente \(b\)).

Desde este punto de vista, dependencia parcial da una interpretación similar a la del análisis usual de coeficientes en regresión lineal, donde pensamos en “todo lo demás constante”.

Igualmente, si el modelo fuera aditivo de la forma \(f(x_1,x_2) = h_1(x_1) + h_2(x_2)\) obtendríamos \[f_1(x_1) = E_{x_2}[h_1(x_1) + h_2(x_2)] = \mu + h_1(x_1),\] y recuperaríamos otra vez la interpetación de “todo lo demás constante”.

Para una variable categórica las gráficas de dependencia parcial se ven como sigue. Escribimos las cantidades logarítmicas en la escala original:

dep_parcial <- plot(mod_2, 2, return.grid = TRUE) %>% arrange(y)
dep_parcial$vNeighborhood <- reorder(dep_parcial$vNeighborhood, dep_parcial$y)
ggplot(dep_parcial, aes(x = vNeighborhood, y = exp(y))) + geom_point() +
    coord_flip()

En general, si nuestro predictor depende de más variables \(f(x_1,x_2, \ldots, x_p)\) entrada. Podemos considerar las funciones \[{f}_{j}(x_j) = E_{(x_1,x_2, \ldots x_p) - x_j}[f(x_1,x_2, \ldots, x_p)],\] que es el valor esperado de \(f(x)\) fijando \(x_j\), y promediando sobre el resto de las variables. Si tenemos una muestra de entrenamiento, podríamos estimarla promediando sobre la muestra de entrenamiento

\[\bar{f}_j(x_j) = \frac{1}{n}\sum_{i=1}^n f(x_1^{(i)}, x_2^{(i)}, \ldots, x_{j-1}^{(i)},\, x_j,\, x_{j+1}^{(i)},\ldots, x_p^{(i)}).\]

Podemos hacer también gráficas de dependencia parcial para más de una variable, si fijamos un subconjunto de variables y promediamos sobre el resto.

plot(mod_2, c(1,3))

Que también podemos graficar como

grid_dp <- plot(mod_2, c(1,3), level.plot = FALSE, return.grid = TRUE)
ggplot(grid_dp, aes(x = vGrLivArea, y = y, 
        colour = vOverallQual, group = vOverallQual)) + geom_line() +
    xlim(c(0, 3000))

## Warning: Removed 5000 rows containing missing values (geom_path).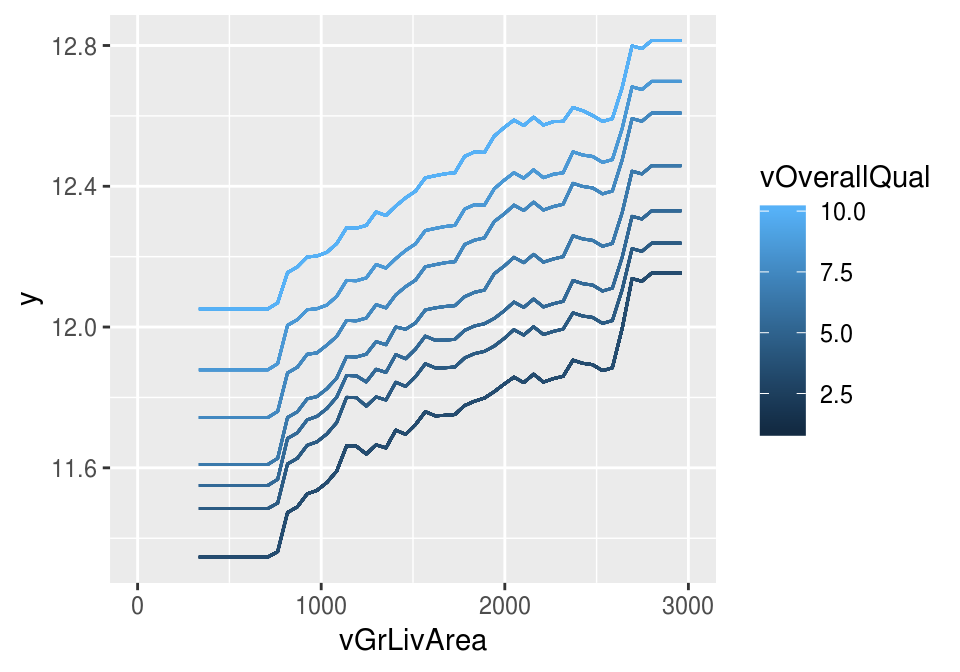

En este caso, no vemos interacciones grandes (GrLivArea y OverallQual) en nuestro modelo.

Más de interpretación

Es importante evitar la interpretación incorrecta de que la función de dependencia parcial da el valor esperado del predictor condicionado a valores de la variable cuya dependencia examinamos. Es decir, \[f_1(x_1) = E_{x_2}(f(x_1,x_2)) \neq E(f(x_1,x_2)|x_1).\] La última cantidad es un valor esperado diferente (calculado sobre la condicional de \(x_2\) dada \(x_1\)), de manera que utiliza información acerca de la relación que hay entre \(x_1\) y \(x_2\), y se puede interpretar como el valor esperado del predictor ingorando \(x_2\). La función de dependencia parcial da el efecto de \(x_1\) tomando en cuenta los efectos promedio de las otras variables.

Ejemplos

Considramos \(f(x_1,x_2) = h_1(x_1)h_2(x_2) = x_1x_2\), donde \(x_1\) y \(x_2\) tienen medias \(a_1\) y \(a_2\). La función de dependiencia parcial de \(x_1\) es (demuéstralo): \(\bar{f}_1(x_1) = a_2 x_1,\) que nos muestra el efecto de \(x_1\) promediando sobre \(x_2\). Sin embargo, la condicional de la predicción dada \(x_1\) es diferente: \[f_1(x_1) = E(x_1x_2 | x_1) = x_1 E(x_2 | x_1)\] y el valor esperado condicional puede ser una función complicada. Por ejemplo, si hay correlación lineal entre \(x_1\) y \(x_2\) podríamos tener \(E(x_2 | x_1) = ax_1 + b\), etc. Esta cantidad tiene sus usos (por ejemplo, hacer predicciones cuando no tenemos \(x_2\)), pero para entender el efecto univariado de \(x_1\) generalmente es más fácil considerar la función de dependiencia parcial.

Finalmente, nótese que cuando hay interacciones fuertes entre las variables, ningún análisis marginal (dependencia parcial o examen de coeficientes) da un resultado tan fácilmente interpretabl. La única solución es considerar el efecto conjunto de las variables que interactúan. De modo que este tipo de análisis funciona mejor cuando no hay interacciones grandes entre las variables (es cercano a un modelo aditivo con efectos no lineales).

13.9.2 Gráficas de dependencia parcial para otros modelos

Como dijimos en la introducción, las gráficas de dependiencia parcial pueden utilizarse para cualquier tipo de modelo.

13.9.2.1 Ejemplo: regresión lineal

¿Qué esperamos si aplicamos a un modelo de regresión lineal?

library(pdp)

## 
## Attaching package: 'pdp'

## The following object is masked from 'package:purrr':
## 
##     partial

mod_lm <- lm(log(vSalePrice) ~ vGrLivArea +vNeighborhood  +
                 vOverallQual + vBsmtFinSF1, entrena)
mod_lm

## 
## Call:
## lm(formula = log(vSalePrice) ~ vGrLivArea + vNeighborhood + vOverallQual + 
##     vBsmtFinSF1, data = entrena)
## 
## Coefficients:
##          (Intercept)            vGrLivArea   vNeighborhoodBrDale  
##           10.9781318             0.0002519            -0.3876381  
## vNeighborhoodBrkSide  vNeighborhoodClearCr  vNeighborhoodCollgCr  
##           -0.1931159             0.0784516             0.0131924  
## vNeighborhoodCrawfor  vNeighborhoodEdwards  vNeighborhoodGilbert  
##            0.0180111            -0.2231209             0.0006351  
##  vNeighborhoodIDOTRR  vNeighborhoodMeadowV  vNeighborhoodMitchel  
##           -0.3716332            -0.3176807            -0.0713348  
##   vNeighborhoodNAmes  vNeighborhoodNoRidge  vNeighborhoodNridgHt  
##           -0.0981734             0.0806283             0.1502544  
##  vNeighborhoodNWAmes  vNeighborhoodOldTown    vNeighborhoodOtros  
##           -0.0528433            -0.2732835            -0.1615437  
##  vNeighborhoodSawyer  vNeighborhoodSawyerW  vNeighborhoodSomerst  
##           -0.0956738            -0.0621679             0.0521564  
## vNeighborhoodStoneBr    vNeighborhoodSWISU   vNeighborhoodTimber  
##            0.1231436            -0.2302935             0.0593881  
## vNeighborhoodVeenker          vOverallQual           vBsmtFinSF1  
##            0.1294244             0.1129118             0.0001089

mod_lm %>%
    partial(pred.var = "vGrLivArea") %>%
    autoplot(rug = TRUE, train = entrena)

13.9.2.2 Ejemplo: bosque aleatorio

library(randomForest)
mod_bosque <- randomForest(log(vSalePrice) ~ vGrLivArea +vNeighborhood  +
                 vOverallQual + vBsmtFinSF1, data = entrena)
mod_bosque

## 
## Call:
##  randomForest(formula = log(vSalePrice) ~ vGrLivArea + vNeighborhood +      vOverallQual + vBsmtFinSF1, data = entrena) 
##                Type of random forest: regression
##                      Number of trees: 500
## No. of variables tried at each split: 1
## 
##           Mean of squared residuals: 0.02367802
##                     % Var explained: 85.15

mod_bosque %>%
    partial(pred.var = "vGrLivArea") %>%
    autoplot(rug = TRUE, train = entrena)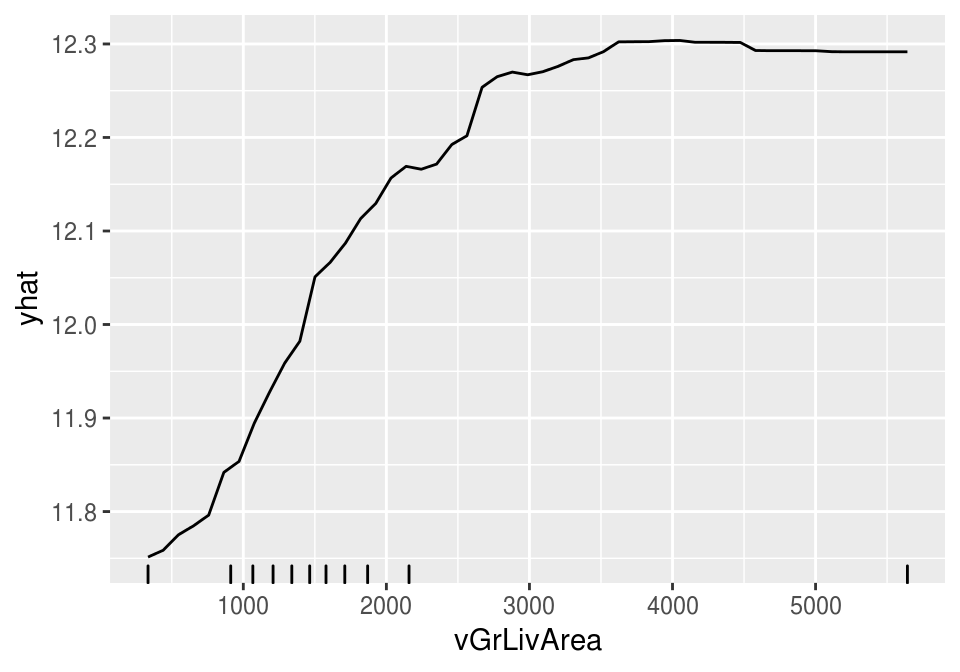

mod_bosque %>%
    partial(pred.var = c("vGrLivArea", "vOverallQual")) %>%
    autoplot(rug = TRUE, train = entrena)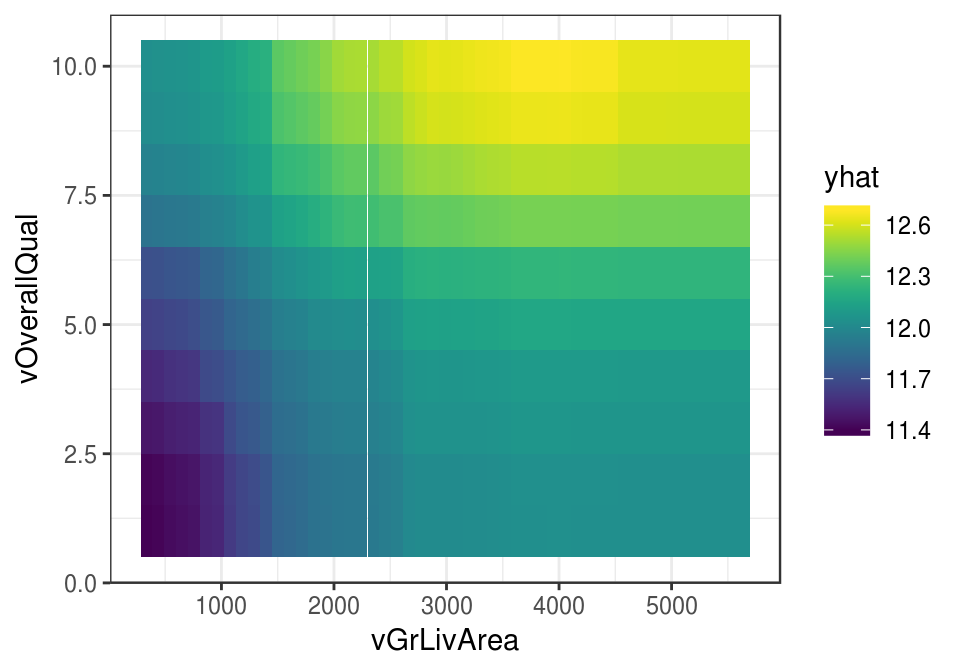

Puedes ver más técnicas en Interpretable Machine Learning, por ejemplo.

13.10 xgboost y gbm

Los paquetes xgboost y gbm parecen ser los más populares para hacer gradient boosting. xgboost, adicionalmente, parece ser más rápido y más flexible que gbm (paralelización, uso de GPU integrado). Existe una lista considerable de competencias de predicción donde el algoritmo/implementación ganadora es xgboost.

library(xgboost)

## 
## Attaching package: 'xgboost'

## The following object is masked from 'package:dplyr':
## 
##     slice

x <- entrena %>% select(-vSalePrice) %>% model.matrix(~., .)
x_entrena <- x[1:1100, ]
x_valida <- x[1101:1460, ]
set.seed(1293)
d_entrena <- xgb.DMatrix(x_entrena, label = log(entrena$vSalePrice[1:1100])) 
d_valida <- xgb.DMatrix(x_valida, label = log(entrena$vSalePrice[1101:1460])) 
watchlist <- list(eval = d_valida, train = d_entrena)
params <- list(booster = "gbtree",
               max_depth = 3, 
               eta = 0.03, 
               nthread = 1, 
               subsample = 0.75, 
               lambda = 0.001,
               objective = "reg:linear", 
               eval_metric = "mae") # error absoluto
bst <- xgb.train(params, d_entrena, nrounds = 1000, watchlist = watchlist, verbose=1)

## [1]  eval-mae:11.176984  train-mae:11.178999 
## [2]  eval-mae:10.841721  train-mae:10.843556 
## [3]  eval-mae:10.516091  train-mae:10.518085 
## [4]  eval-mae:10.200583  train-mae:10.202491 
## [5]  eval-mae:9.894920   train-mae:9.896530 
## [6]  eval-mae:9.598317   train-mae:9.599773 
## [7]  eval-mae:9.310502   train-mae:9.311866 
## [8]  eval-mae:9.031566   train-mae:9.032389 
## [9]  eval-mae:8.760724   train-mae:8.761462 
## [10] eval-mae:8.498172   train-mae:8.498637 
## [11] eval-mae:8.243278   train-mae:8.243702 
## [12] eval-mae:7.996028   train-mae:7.996329 
## [13] eval-mae:7.756287   train-mae:7.756411 
## [14] eval-mae:7.523738   train-mae:7.523695 
## [15] eval-mae:7.298147   train-mae:7.298057 
## [16] eval-mae:7.079457   train-mae:7.079143 
## [17] eval-mae:6.867540   train-mae:6.866744 
## [18] eval-mae:6.661871   train-mae:6.660701 
## [19] eval-mae:6.462197   train-mae:6.460776 
## [20] eval-mae:6.268476   train-mae:6.266927 
## [21] eval-mae:6.080146   train-mae:6.078687 
## [22] eval-mae:5.897626   train-mae:5.896358 
## [23] eval-mae:5.720685   train-mae:5.719357 
## [24] eval-mae:5.549398   train-mae:5.547802 
## [25] eval-mae:5.382868   train-mae:5.381410 
## [26] eval-mae:5.221207   train-mae:5.219763 
## [27] eval-mae:5.064470   train-mae:5.063203 
## [28] eval-mae:4.912503   train-mae:4.911200 
## [29] eval-mae:4.764926   train-mae:4.763807 
## [30] eval-mae:4.622063   train-mae:4.620884 
## [31] eval-mae:4.483413   train-mae:4.482223 
## [32] eval-mae:4.348776   train-mae:4.347674 
## [33] eval-mae:4.218169   train-mae:4.217224 
## [34] eval-mae:4.091733   train-mae:4.090778 
## [35] eval-mae:3.968975   train-mae:3.968010 
## [36] eval-mae:3.849841   train-mae:3.848888 
## [37] eval-mae:3.734298   train-mae:3.733345 
## [38] eval-mae:3.622312   train-mae:3.621352 
## [39] eval-mae:3.513997   train-mae:3.512828 
## [40] eval-mae:3.408348   train-mae:3.407215 
## [41] eval-mae:3.306162   train-mae:3.304984 
## [42] eval-mae:3.206973   train-mae:3.205757 
## [43] eval-mae:3.110841   train-mae:3.109580 
## [44] eval-mae:3.017576   train-mae:3.016211 
## [45] eval-mae:2.926954   train-mae:2.925621 
## [46] eval-mae:2.839241   train-mae:2.837812 
## [47] eval-mae:2.754123   train-mae:2.752701 
## [48] eval-mae:2.671518   train-mae:2.670100 
## [49] eval-mae:2.591545   train-mae:2.590034 
## [50] eval-mae:2.513927   train-mae:2.512405 
## [51] eval-mae:2.438531   train-mae:2.437090 
## [52] eval-mae:2.365263   train-mae:2.363928 
## [53] eval-mae:2.294239   train-mae:2.292855 
## [54] eval-mae:2.225363   train-mae:2.224102 
## [55] eval-mae:2.158767   train-mae:2.157321 
## [56] eval-mae:2.093980   train-mae:2.092589 
## [57] eval-mae:2.031284   train-mae:2.029821 
## [58] eval-mae:1.970396   train-mae:1.969090 
## [59] eval-mae:1.911263   train-mae:1.910023 
## [60] eval-mae:1.854034   train-mae:1.852790 
## [61] eval-mae:1.798455   train-mae:1.797090 
## [62] eval-mae:1.744618   train-mae:1.743325 
## [63] eval-mae:1.692358   train-mae:1.691019 
## [64] eval-mae:1.641327   train-mae:1.640058 
## [65] eval-mae:1.592239   train-mae:1.590907 
## [66] eval-mae:1.544698   train-mae:1.543235 
## [67] eval-mae:1.498477   train-mae:1.496958 
## [68] eval-mae:1.453635   train-mae:1.452130 
## [69] eval-mae:1.409772   train-mae:1.408428 
## [70] eval-mae:1.367715   train-mae:1.366239 
## [71] eval-mae:1.326800   train-mae:1.325253 
## [72] eval-mae:1.287248   train-mae:1.285523 
## [73] eval-mae:1.248763   train-mae:1.246932 
## [74] eval-mae:1.211261   train-mae:1.209524 
## [75] eval-mae:1.174987   train-mae:1.173262 
## [76] eval-mae:1.139906   train-mae:1.138175 
## [77] eval-mae:1.105752   train-mae:1.104045 
## [78] eval-mae:1.072770   train-mae:1.070972 
## [79] eval-mae:1.040598   train-mae:1.038826 
## [80] eval-mae:1.009650   train-mae:1.007721 
## [81] eval-mae:0.979265   train-mae:0.977407 
## [82] eval-mae:0.950001   train-mae:0.948159 
## [83] eval-mae:0.921491   train-mae:0.919640 
## [84] eval-mae:0.894094   train-mae:0.892078 
## [85] eval-mae:0.867323   train-mae:0.865286 
## [86] eval-mae:0.841607   train-mae:0.839350 
## [87] eval-mae:0.816515   train-mae:0.814126 
## [88] eval-mae:0.792066   train-mae:0.789763 
## [89] eval-mae:0.768292   train-mae:0.766059 
## [90] eval-mae:0.745335   train-mae:0.743182 
## [91] eval-mae:0.723135   train-mae:0.720921 
## [92] eval-mae:0.701431   train-mae:0.699273 
## [93] eval-mae:0.680305   train-mae:0.678268 
## [94] eval-mae:0.659951   train-mae:0.657979 
## [95] eval-mae:0.640289   train-mae:0.638384 
## [96] eval-mae:0.621096   train-mae:0.619237 
## [97] eval-mae:0.602619   train-mae:0.600687 
## [98] eval-mae:0.584839   train-mae:0.582761 
## [99] eval-mae:0.567640   train-mae:0.565343 
## [100]    eval-mae:0.550959   train-mae:0.548542 
## [101]    eval-mae:0.534757   train-mae:0.532259 
## [102]    eval-mae:0.519005   train-mae:0.516405 
## [103]    eval-mae:0.503871   train-mae:0.501128 
## [104]    eval-mae:0.489255   train-mae:0.486071 
## [105]    eval-mae:0.475083   train-mae:0.471560 
## [106]    eval-mae:0.461362   train-mae:0.457412 
## [107]    eval-mae:0.448123   train-mae:0.443822 
## [108]    eval-mae:0.435431   train-mae:0.430689 
## [109]    eval-mae:0.422947   train-mae:0.418007 
## [110]    eval-mae:0.410675   train-mae:0.405594 
## [111]    eval-mae:0.399015   train-mae:0.393689 
## [112]    eval-mae:0.387629   train-mae:0.382120 
## [113]    eval-mae:0.376682   train-mae:0.370912 
## [114]    eval-mae:0.366002   train-mae:0.359868 
## [115]    eval-mae:0.355613   train-mae:0.349159 
## [116]    eval-mae:0.345714   train-mae:0.338928 
## [117]    eval-mae:0.336081   train-mae:0.328886 
## [118]    eval-mae:0.326819   train-mae:0.319230 
## [119]    eval-mae:0.317691   train-mae:0.309853 
## [120]    eval-mae:0.308935   train-mae:0.300856 
## [121]    eval-mae:0.300444   train-mae:0.292126 
## [122]    eval-mae:0.292296   train-mae:0.283533 
## [123]    eval-mae:0.284549   train-mae:0.275342 
## [124]    eval-mae:0.277110   train-mae:0.267480 
## [125]    eval-mae:0.269827   train-mae:0.259787 
## [126]    eval-mae:0.262780   train-mae:0.252439 
## [127]    eval-mae:0.255950   train-mae:0.245250 
## [128]    eval-mae:0.249369   train-mae:0.238362 
## [129]    eval-mae:0.242996   train-mae:0.231782 
## [130]    eval-mae:0.236763   train-mae:0.225267 
## [131]    eval-mae:0.230745   train-mae:0.219100 
## [132]    eval-mae:0.225008   train-mae:0.213131 
## [133]    eval-mae:0.219477   train-mae:0.207348 
## [134]    eval-mae:0.214161   train-mae:0.201821 
## [135]    eval-mae:0.208863   train-mae:0.196452 
## [136]    eval-mae:0.203891   train-mae:0.191283 
## [137]    eval-mae:0.198914   train-mae:0.186304 
## [138]    eval-mae:0.194195   train-mae:0.181375 
## [139]    eval-mae:0.189724   train-mae:0.176576 
## [140]    eval-mae:0.185307   train-mae:0.171958 
## [141]    eval-mae:0.181102   train-mae:0.167600 
## [142]    eval-mae:0.177018   train-mae:0.163403 
## [143]    eval-mae:0.173138   train-mae:0.159351 
## [144]    eval-mae:0.169522   train-mae:0.155450 
## [145]    eval-mae:0.165944   train-mae:0.151665 
## [146]    eval-mae:0.162522   train-mae:0.148044 
## [147]    eval-mae:0.159126   train-mae:0.144454 
## [148]    eval-mae:0.155916   train-mae:0.140983 
## [149]    eval-mae:0.152798   train-mae:0.137733 
## [150]    eval-mae:0.149890   train-mae:0.134611 
## [151]    eval-mae:0.147011   train-mae:0.131581 
## [152]    eval-mae:0.144343   train-mae:0.128727 
## [153]    eval-mae:0.141851   train-mae:0.126030 
## [154]    eval-mae:0.139432   train-mae:0.123388 
## [155]    eval-mae:0.137020   train-mae:0.120825 
## [156]    eval-mae:0.134766   train-mae:0.118328 
## [157]    eval-mae:0.132575   train-mae:0.115898 
## [158]    eval-mae:0.130664   train-mae:0.113702 
## [159]    eval-mae:0.128784   train-mae:0.111465 
## [160]    eval-mae:0.126796   train-mae:0.109349 
## [161]    eval-mae:0.125017   train-mae:0.107313 
## [162]    eval-mae:0.123313   train-mae:0.105365 
## [163]    eval-mae:0.121812   train-mae:0.103522 
## [164]    eval-mae:0.120360   train-mae:0.101748 
## [165]    eval-mae:0.118789   train-mae:0.100075 
## [166]    eval-mae:0.117342   train-mae:0.098434 
## [167]    eval-mae:0.116027   train-mae:0.096974 
## [168]    eval-mae:0.114808   train-mae:0.095542 
## [169]    eval-mae:0.113652   train-mae:0.094151 
## [170]    eval-mae:0.112540   train-mae:0.092748 
## [171]    eval-mae:0.111490   train-mae:0.091464 
## [172]    eval-mae:0.110391   train-mae:0.090240 
## [173]    eval-mae:0.109336   train-mae:0.089060 
## [174]    eval-mae:0.108291   train-mae:0.087905 
## [175]    eval-mae:0.107341   train-mae:0.086859 
## [176]    eval-mae:0.106423   train-mae:0.085829 
## [177]    eval-mae:0.105520   train-mae:0.084811 
## [178]    eval-mae:0.104731   train-mae:0.083838 
## [179]    eval-mae:0.104073   train-mae:0.083000 
## [180]    eval-mae:0.103307   train-mae:0.082091 
## [181]    eval-mae:0.102615   train-mae:0.081298 
## [182]    eval-mae:0.102002   train-mae:0.080498 
## [183]    eval-mae:0.101427   train-mae:0.079755 
## [184]    eval-mae:0.100969   train-mae:0.079049 
## [185]    eval-mae:0.100446   train-mae:0.078360 
## [186]    eval-mae:0.100050   train-mae:0.077707 
## [187]    eval-mae:0.099440   train-mae:0.077120 
## [188]    eval-mae:0.098967   train-mae:0.076555 
## [189]    eval-mae:0.098478   train-mae:0.075945 
## [190]    eval-mae:0.098064   train-mae:0.075435 
## [191]    eval-mae:0.097584   train-mae:0.074891 
## [192]    eval-mae:0.097268   train-mae:0.074412 
## [193]    eval-mae:0.096946   train-mae:0.073957 
## [194]    eval-mae:0.096569   train-mae:0.073517 
## [195]    eval-mae:0.096221   train-mae:0.073024 
## [196]    eval-mae:0.095884   train-mae:0.072631 
## [197]    eval-mae:0.095583   train-mae:0.072257 
## [198]    eval-mae:0.095326   train-mae:0.071892 
## [199]    eval-mae:0.095087   train-mae:0.071487 
## [200]    eval-mae:0.094727   train-mae:0.071093 
## [201]    eval-mae:0.094426   train-mae:0.070704 
## [202]    eval-mae:0.094213   train-mae:0.070354 
## [203]    eval-mae:0.093980   train-mae:0.070053 
## [204]    eval-mae:0.093653   train-mae:0.069705 
## [205]    eval-mae:0.093427   train-mae:0.069476 
## [206]    eval-mae:0.093285   train-mae:0.069242 
## [207]    eval-mae:0.093102   train-mae:0.068947 
## [208]    eval-mae:0.092898   train-mae:0.068708 
## [209]    eval-mae:0.092622   train-mae:0.068512 
## [210]    eval-mae:0.092443   train-mae:0.068279 
## [211]    eval-mae:0.092221   train-mae:0.068082 
## [212]    eval-mae:0.092098   train-mae:0.067902 
## [213]    eval-mae:0.091922   train-mae:0.067684 
## [214]    eval-mae:0.091705   train-mae:0.067478 
## [215]    eval-mae:0.091618   train-mae:0.067311 
## [216]    eval-mae:0.091529   train-mae:0.067056 
## [217]    eval-mae:0.091330   train-mae:0.066887 
## [218]    eval-mae:0.091146   train-mae:0.066725 
## [219]    eval-mae:0.091042   train-mae:0.066575 
## [220]    eval-mae:0.090911   train-mae:0.066396 
## [221]    eval-mae:0.090879   train-mae:0.066248 
## [222]    eval-mae:0.090784   train-mae:0.066083 
## [223]    eval-mae:0.090649   train-mae:0.065939 
## [224]    eval-mae:0.090566   train-mae:0.065818 
## [225]    eval-mae:0.090553   train-mae:0.065679 
## [226]    eval-mae:0.090387   train-mae:0.065510 
## [227]    eval-mae:0.090297   train-mae:0.065415 
## [228]    eval-mae:0.090133   train-mae:0.065294 
## [229]    eval-mae:0.090028   train-mae:0.065166 
## [230]    eval-mae:0.089975   train-mae:0.065034 
## [231]    eval-mae:0.089858   train-mae:0.064864 
## [232]    eval-mae:0.089758   train-mae:0.064732 
## [233]    eval-mae:0.089635   train-mae:0.064615 
## [234]    eval-mae:0.089514   train-mae:0.064502 
## [235]    eval-mae:0.089433   train-mae:0.064429 
## [236]    eval-mae:0.089307   train-mae:0.064289 
## [237]    eval-mae:0.089243   train-mae:0.064163 
## [238]    eval-mae:0.089158   train-mae:0.064053 
## [239]    eval-mae:0.089103   train-mae:0.063912 
## [240]    eval-mae:0.088984   train-mae:0.063769 
## [241]    eval-mae:0.088899   train-mae:0.063658 
## [242]    eval-mae:0.088844   train-mae:0.063538 
## [243]    eval-mae:0.088773   train-mae:0.063402 
## [244]    eval-mae:0.088694   train-mae:0.063309 
## [245]    eval-mae:0.088552   train-mae:0.063216 
## [246]    eval-mae:0.088483   train-mae:0.063079 
## [247]    eval-mae:0.088426   train-mae:0.062929 
## [248]    eval-mae:0.088428   train-mae:0.062880 
## [249]    eval-mae:0.088324   train-mae:0.062803 
## [250]    eval-mae:0.088255   train-mae:0.062691 
## [251]    eval-mae:0.088286   train-mae:0.062589 
## [252]    eval-mae:0.088173   train-mae:0.062481 
## [253]    eval-mae:0.088107   train-mae:0.062389 
## [254]    eval-mae:0.088114   train-mae:0.062245 
## [255]    eval-mae:0.087986   train-mae:0.062171 
## [256]    eval-mae:0.087940   train-mae:0.062072 
## [257]    eval-mae:0.087850   train-mae:0.061937 
## [258]    eval-mae:0.087858   train-mae:0.061872 
## [259]    eval-mae:0.087836   train-mae:0.061784 
## [260]    eval-mae:0.087886   train-mae:0.061682 
## [261]    eval-mae:0.087875   train-mae:0.061586 
## [262]    eval-mae:0.087792   train-mae:0.061518 
## [263]    eval-mae:0.087855   train-mae:0.061449 
## [264]    eval-mae:0.087852   train-mae:0.061385 
## [265]    eval-mae:0.087874   train-mae:0.061345 
## [266]    eval-mae:0.087845   train-mae:0.061241 
## [267]    eval-mae:0.087827   train-mae:0.061160 
## [268]    eval-mae:0.087786   train-mae:0.061073 
## [269]    eval-mae:0.087769   train-mae:0.060986 
## [270]    eval-mae:0.087661   train-mae:0.060906 
## [271]    eval-mae:0.087615   train-mae:0.060839 
## [272]    eval-mae:0.087578   train-mae:0.060745 
## [273]    eval-mae:0.087529   train-mae:0.060659 
## [274]    eval-mae:0.087554   train-mae:0.060569 
## [275]    eval-mae:0.087489   train-mae:0.060491 
## [276]    eval-mae:0.087411   train-mae:0.060398 
## [277]    eval-mae:0.087333   train-mae:0.060327 
## [278]    eval-mae:0.087272   train-mae:0.060290 
## [279]    eval-mae:0.087254   train-mae:0.060206 
## [280]    eval-mae:0.087197   train-mae:0.060154 
## [281]    eval-mae:0.087200   train-mae:0.060103 
## [282]    eval-mae:0.087172   train-mae:0.060053 
## [283]    eval-mae:0.087125   train-mae:0.059954 
## [284]    eval-mae:0.087026   train-mae:0.059857 
## [285]    eval-mae:0.086999   train-mae:0.059762 
## [286]    eval-mae:0.086915   train-mae:0.059643 
## [287]    eval-mae:0.086855   train-mae:0.059590 
## [288]    eval-mae:0.086838   train-mae:0.059497 
## [289]    eval-mae:0.086809   train-mae:0.059417 
## [290]    eval-mae:0.086732   train-mae:0.059345 
## [291]    eval-mae:0.086776   train-mae:0.059269 
## [292]    eval-mae:0.086760   train-mae:0.059201 
## [293]    eval-mae:0.086720   train-mae:0.059145 
## [294]    eval-mae:0.086673   train-mae:0.059100 
## [295]    eval-mae:0.086609   train-mae:0.059041 
## [296]    eval-mae:0.086595   train-mae:0.058986 
## [297]    eval-mae:0.086593   train-mae:0.058957 
## [298]    eval-mae:0.086586   train-mae:0.058895 
## [299]    eval-mae:0.086577   train-mae:0.058870 
## [300]    eval-mae:0.086516   train-mae:0.058809 
## [301]    eval-mae:0.086485   train-mae:0.058778 
## [302]    eval-mae:0.086479   train-mae:0.058720 
## [303]    eval-mae:0.086427   train-mae:0.058670 
## [304]    eval-mae:0.086438   train-mae:0.058585 
## [305]    eval-mae:0.086284   train-mae:0.058460 
## [306]    eval-mae:0.086287   train-mae:0.058395 
## [307]    eval-mae:0.086234   train-mae:0.058296 
## [308]    eval-mae:0.086151   train-mae:0.058170 
## [309]    eval-mae:0.086172   train-mae:0.058146 
## [310]    eval-mae:0.086082   train-mae:0.058028 
## [311]    eval-mae:0.086119   train-mae:0.057975 
## [312]    eval-mae:0.085976   train-mae:0.057914 
## [313]    eval-mae:0.086000   train-mae:0.057830 
## [314]    eval-mae:0.085938   train-mae:0.057790 
## [315]    eval-mae:0.085945   train-mae:0.057748 
## [316]    eval-mae:0.085901   train-mae:0.057673 
## [317]    eval-mae:0.085880   train-mae:0.057618 
## [318]    eval-mae:0.085865   train-mae:0.057565 
## [319]    eval-mae:0.085865   train-mae:0.057540 
## [320]    eval-mae:0.085835   train-mae:0.057481 
## [321]    eval-mae:0.085732   train-mae:0.057387 
## [322]    eval-mae:0.085633   train-mae:0.057302 
## [323]    eval-mae:0.085625   train-mae:0.057261 
## [324]    eval-mae:0.085565   train-mae:0.057225 
## [325]    eval-mae:0.085518   train-mae:0.057109 
## [326]    eval-mae:0.085518   train-mae:0.057035 
## [327]    eval-mae:0.085509   train-mae:0.056989 
## [328]    eval-mae:0.085450   train-mae:0.056925 
## [329]    eval-mae:0.085354   train-mae:0.056854 
## [330]    eval-mae:0.085405   train-mae:0.056818 
## [331]    eval-mae:0.085403   train-mae:0.056759 
## [332]    eval-mae:0.085380   train-mae:0.056720 
## [333]    eval-mae:0.085301   train-mae:0.056663 
## [334]    eval-mae:0.085302   train-mae:0.056629 
## [335]    eval-mae:0.085303   train-mae:0.056604 
## [336]    eval-mae:0.085306   train-mae:0.056546 
## [337]    eval-mae:0.085299   train-mae:0.056521 
## [338]    eval-mae:0.085303   train-mae:0.056471 
## [339]    eval-mae:0.085293   train-mae:0.056430 
## [340]    eval-mae:0.085250   train-mae:0.056383 
## [341]    eval-mae:0.085262   train-mae:0.056357 
## [342]    eval-mae:0.085198   train-mae:0.056260 
## [343]    eval-mae:0.085143   train-mae:0.056180 
## [344]    eval-mae:0.085119   train-mae:0.056119 
## [345]    eval-mae:0.085114   train-mae:0.056049 
## [346]    eval-mae:0.085076   train-mae:0.055955 
## [347]    eval-mae:0.085052   train-mae:0.055891 
## [348]    eval-mae:0.084995   train-mae:0.055784 
## [349]    eval-mae:0.084884   train-mae:0.055763 
## [350]    eval-mae:0.084881   train-mae:0.055723 
## [351]    eval-mae:0.084850   train-mae:0.055677 
## [352]    eval-mae:0.084835   train-mae:0.055634 
## [353]    eval-mae:0.084813   train-mae:0.055604 
## [354]    eval-mae:0.084814   train-mae:0.055518 
## [355]    eval-mae:0.084729   train-mae:0.055429 
## [356]    eval-mae:0.084664   train-mae:0.055366 
## [357]    eval-mae:0.084641   train-mae:0.055308 
## [358]    eval-mae:0.084652   train-mae:0.055266 
## [359]    eval-mae:0.084666   train-mae:0.055200 
## [360]    eval-mae:0.084570   train-mae:0.055146 
## [361]    eval-mae:0.084525   train-mae:0.055081 
## [362]    eval-mae:0.084480   train-mae:0.055013 
## [363]    eval-mae:0.084481   train-mae:0.054947 
## [364]    eval-mae:0.084424   train-mae:0.054909 
## [365]    eval-mae:0.084447   train-mae:0.054874 
## [366]    eval-mae:0.084462   train-mae:0.054830 
## [367]    eval-mae:0.084453   train-mae:0.054784 
## [368]    eval-mae:0.084497   train-mae:0.054713 
## [369]    eval-mae:0.084524   train-mae:0.054628 
## [370]    eval-mae:0.084564   train-mae:0.054578 
## [371]    eval-mae:0.084652   train-mae:0.054503 
## [372]    eval-mae:0.084584   train-mae:0.054418 
## [373]    eval-mae:0.084584   train-mae:0.054359 
## [374]    eval-mae:0.084543   train-mae:0.054309 
## [375]    eval-mae:0.084549   train-mae:0.054245 
## [376]    eval-mae:0.084527   train-mae:0.054191 
## [377]    eval-mae:0.084571   train-mae:0.054131 
## [378]    eval-mae:0.084512   train-mae:0.054093 
## [379]    eval-mae:0.084489   train-mae:0.054033 
## [380]    eval-mae:0.084500   train-mae:0.053985 
## [381]    eval-mae:0.084476   train-mae:0.053950 
## [382]    eval-mae:0.084487   train-mae:0.053913 
## [383]    eval-mae:0.084448   train-mae:0.053867 
## [384]    eval-mae:0.084456   train-mae:0.053785 
## [385]    eval-mae:0.084410   train-mae:0.053715 
## [386]    eval-mae:0.084386   train-mae:0.053668 
## [387]    eval-mae:0.084407   train-mae:0.053649 
## [388]    eval-mae:0.084424   train-mae:0.053626 
## [389]    eval-mae:0.084410   train-mae:0.053594 
## [390]    eval-mae:0.084467   train-mae:0.053542 
## [391]    eval-mae:0.084463   train-mae:0.053521 
## [392]    eval-mae:0.084370   train-mae:0.053448 
## [393]    eval-mae:0.084482   train-mae:0.053389 
## [394]    eval-mae:0.084497   train-mae:0.053355 
## [395]    eval-mae:0.084482   train-mae:0.053313 
## [396]    eval-mae:0.084498   train-mae:0.053266 
## [397]    eval-mae:0.084478   train-mae:0.053233 
## [398]    eval-mae:0.084425   train-mae:0.053193 
## [399]    eval-mae:0.084415   train-mae:0.053149 
## [400]    eval-mae:0.084407   train-mae:0.053104 
## [401]    eval-mae:0.084395   train-mae:0.053061 
## [402]    eval-mae:0.084426   train-mae:0.053023 
## [403]    eval-mae:0.084408   train-mae:0.052971 
## [404]    eval-mae:0.084358   train-mae:0.052871 
## [405]    eval-mae:0.084301   train-mae:0.052844 
## [406]    eval-mae:0.084331   train-mae:0.052780 
## [407]    eval-mae:0.084369   train-mae:0.052714 
## [408]    eval-mae:0.084420   train-mae:0.052650 
## [409]    eval-mae:0.084449   train-mae:0.052608 
## [410]    eval-mae:0.084383   train-mae:0.052540 
## [411]    eval-mae:0.084424   train-mae:0.052486 
## [412]    eval-mae:0.084369   train-mae:0.052419 
## [413]    eval-mae:0.084357   train-mae:0.052369 
## [414]    eval-mae:0.084351   train-mae:0.052343 
## [415]    eval-mae:0.084340   train-mae:0.052329 
## [416]    eval-mae:0.084311   train-mae:0.052281 
## [417]    eval-mae:0.084291   train-mae:0.052225 
## [418]    eval-mae:0.084283   train-mae:0.052165 
## [419]    eval-mae:0.084310   train-mae:0.052132 
## [420]    eval-mae:0.084325   train-mae:0.052103 
## [421]    eval-mae:0.084254   train-mae:0.052044 
## [422]    eval-mae:0.084209   train-mae:0.051979 
## [423]    eval-mae:0.084190   train-mae:0.051961 
## [424]    eval-mae:0.084179   train-mae:0.051901 
## [425]    eval-mae:0.084110   train-mae:0.051819 
## [426]    eval-mae:0.084115   train-mae:0.051767 
## [427]    eval-mae:0.084119   train-mae:0.051744 
## [428]    eval-mae:0.084201   train-mae:0.051716 
## [429]    eval-mae:0.084185   train-mae:0.051659 
## [430]    eval-mae:0.084138   train-mae:0.051643 
## [431]    eval-mae:0.084084   train-mae:0.051593 
## [432]    eval-mae:0.084070   train-mae:0.051544 
## [433]    eval-mae:0.084097   train-mae:0.051488 
## [434]    eval-mae:0.084022   train-mae:0.051436 
## [435]    eval-mae:0.084042   train-mae:0.051411 
## [436]    eval-mae:0.084057   train-mae:0.051396 
## [437]    eval-mae:0.084068   train-mae:0.051339 
## [438]    eval-mae:0.084071   train-mae:0.051288 
## [439]    eval-mae:0.084004   train-mae:0.051223 
## [440]    eval-mae:0.083965   train-mae:0.051140 
## [441]    eval-mae:0.083886   train-mae:0.051050 
## [442]    eval-mae:0.083863   train-mae:0.051024 
## [443]    eval-mae:0.083845   train-mae:0.050989 
## [444]    eval-mae:0.083819   train-mae:0.050962 
## [445]    eval-mae:0.083856   train-mae:0.050925 
## [446]    eval-mae:0.083814   train-mae:0.050879 
## [447]    eval-mae:0.083765   train-mae:0.050836 
## [448]    eval-mae:0.083769   train-mae:0.050787 
## [449]    eval-mae:0.083775   train-mae:0.050745 
## [450]    eval-mae:0.083750   train-mae:0.050700 
## [451]    eval-mae:0.083791   train-mae:0.050674 
## [452]    eval-mae:0.083776   train-mae:0.050637 
## [453]    eval-mae:0.083723   train-mae:0.050550 
## [454]    eval-mae:0.083803   train-mae:0.050513 
## [455]    eval-mae:0.083859   train-mae:0.050460 
## [456]    eval-mae:0.083814   train-mae:0.050408 
## [457]    eval-mae:0.083767   train-mae:0.050340 
## [458]    eval-mae:0.083771   train-mae:0.050287 
## [459]    eval-mae:0.083755   train-mae:0.050240 
## [460]    eval-mae:0.083750   train-mae:0.050189 
## [461]    eval-mae:0.083720   train-mae:0.050142 
## [462]    eval-mae:0.083717   train-mae:0.050106 
## [463]    eval-mae:0.083710   train-mae:0.050061 
## [464]    eval-mae:0.083683   train-mae:0.050015 
## [465]    eval-mae:0.083689   train-mae:0.049983 
## [466]    eval-mae:0.083666   train-mae:0.049909 
## [467]    eval-mae:0.083639   train-mae:0.049852 
## [468]    eval-mae:0.083617   train-mae:0.049820 
## [469]    eval-mae:0.083591   train-mae:0.049770 
## [470]    eval-mae:0.083577   train-mae:0.049716 
## [471]    eval-mae:0.083554   train-mae:0.049673 
## [472]    eval-mae:0.083583   train-mae:0.049596 
## [473]    eval-mae:0.083558   train-mae:0.049555 
## [474]    eval-mae:0.083495   train-mae:0.049509 
## [475]    eval-mae:0.083587   train-mae:0.049473 
## [476]    eval-mae:0.083601   train-mae:0.049437 
## [477]    eval-mae:0.083587   train-mae:0.049383 
## [478]    eval-mae:0.083559   train-mae:0.049347 
## [479]    eval-mae:0.083517   train-mae:0.049307 
## [480]    eval-mae:0.083496   train-mae:0.049250 
## [481]    eval-mae:0.083533   train-mae:0.049206 
## [482]    eval-mae:0.083537   train-mae:0.049162 
## [483]    eval-mae:0.083506   train-mae:0.049146 
## [484]    eval-mae:0.083505   train-mae:0.049081 
## [485]    eval-mae:0.083484   train-mae:0.049040 
## [486]    eval-mae:0.083516   train-mae:0.048998 
## [487]    eval-mae:0.083491   train-mae:0.048962 
## [488]    eval-mae:0.083445   train-mae:0.048926 
## [489]    eval-mae:0.083446   train-mae:0.048881 
## [490]    eval-mae:0.083456   train-mae:0.048840 
## [491]    eval-mae:0.083439   train-mae:0.048826 
## [492]    eval-mae:0.083419   train-mae:0.048768 
## [493]    eval-mae:0.083413   train-mae:0.048739 
## [494]    eval-mae:0.083410   train-mae:0.048667 
## [495]    eval-mae:0.083395   train-mae:0.048628 
## [496]    eval-mae:0.083412   train-mae:0.048589 
## [497]    eval-mae:0.083414   train-mae:0.048558 
## [498]    eval-mae:0.083424   train-mae:0.048521 
## [499]    eval-mae:0.083406   train-mae:0.048495 
## [500]    eval-mae:0.083423   train-mae:0.048462 
## [501]    eval-mae:0.083402   train-mae:0.048429 
## [502]    eval-mae:0.083383   train-mae:0.048368 
## [503]    eval-mae:0.083338   train-mae:0.048326 
## [504]    eval-mae:0.083347   train-mae:0.048276 
## [505]    eval-mae:0.083347   train-mae:0.048219 
## [506]    eval-mae:0.083345   train-mae:0.048153 
## [507]    eval-mae:0.083294   train-mae:0.048102 
## [508]    eval-mae:0.083321   train-mae:0.048060 
## [509]    eval-mae:0.083434   train-mae:0.048037 
## [510]    eval-mae:0.083403   train-mae:0.047984 
## [511]    eval-mae:0.083413   train-mae:0.047944 
## [512]    eval-mae:0.083429   train-mae:0.047920 
## [513]    eval-mae:0.083422   train-mae:0.047848 
## [514]    eval-mae:0.083424   train-mae:0.047797 
## [515]    eval-mae:0.083417   train-mae:0.047785 
## [516]    eval-mae:0.083381   train-mae:0.047721 
## [517]    eval-mae:0.083367   train-mae:0.047657 
## [518]    eval-mae:0.083448   train-mae:0.047613 
## [519]    eval-mae:0.083447   train-mae:0.047596 
## [520]    eval-mae:0.083448   train-mae:0.047582 
## [521]    eval-mae:0.083486   train-mae:0.047549 
## [522]    eval-mae:0.083497   train-mae:0.047541 
## [523]    eval-mae:0.083452   train-mae:0.047492 
## [524]    eval-mae:0.083480   train-mae:0.047451 
## [525]    eval-mae:0.083466   train-mae:0.047403 
## [526]    eval-mae:0.083412   train-mae:0.047376 
## [527]    eval-mae:0.083386   train-mae:0.047350 
## [528]    eval-mae:0.083379   train-mae:0.047307 
## [529]    eval-mae:0.083400   train-mae:0.047270 
## [530]    eval-mae:0.083399   train-mae:0.047251 
## [531]    eval-mae:0.083375   train-mae:0.047216 
## [532]    eval-mae:0.083389   train-mae:0.047145 
## [533]    eval-mae:0.083398   train-mae:0.047097 
## [534]    eval-mae:0.083554   train-mae:0.047045 
## [535]    eval-mae:0.083531   train-mae:0.046996 
## [536]    eval-mae:0.083492   train-mae:0.046947 
## [537]    eval-mae:0.083512   train-mae:0.046911 
## [538]    eval-mae:0.083471   train-mae:0.046876 
## [539]    eval-mae:0.083465   train-mae:0.046823 
## [540]    eval-mae:0.083473   train-mae:0.046812 
## [541]    eval-mae:0.083713   train-mae:0.046781 
## [542]    eval-mae:0.083704   train-mae:0.046763 
## [543]    eval-mae:0.083721   train-mae:0.046713 
## [544]    eval-mae:0.083725   train-mae:0.046696 
## [545]    eval-mae:0.083722   train-mae:0.046662 
## [546]    eval-mae:0.083720   train-mae:0.046620 
## [547]    eval-mae:0.083701   train-mae:0.046592 
## [548]    eval-mae:0.083718   train-mae:0.046556 
## [549]    eval-mae:0.083690   train-mae:0.046525 
## [550]    eval-mae:0.083672   train-mae:0.046515 
## [551]    eval-mae:0.083683   train-mae:0.046481 
## [552]    eval-mae:0.083655   train-mae:0.046449 
## [553]    eval-mae:0.083640   train-mae:0.046404 
## [554]    eval-mae:0.083666   train-mae:0.046354 
## [555]    eval-mae:0.083599   train-mae:0.046326 
## [556]    eval-mae:0.083763   train-mae:0.046306 
## [557]    eval-mae:0.083761   train-mae:0.046247 
## [558]    eval-mae:0.083770   train-mae:0.046206 
## [559]    eval-mae:0.083779   train-mae:0.046170 
## [560]    eval-mae:0.083762   train-mae:0.046133 
## [561]    eval-mae:0.083762   train-mae:0.046083 
## [562]    eval-mae:0.083710   train-mae:0.046065 
## [563]    eval-mae:0.083731   train-mae:0.046022 
## [564]    eval-mae:0.083765   train-mae:0.045998 
## [565]    eval-mae:0.083778   train-mae:0.045987 
## [566]    eval-mae:0.083797   train-mae:0.045909 
## [567]    eval-mae:0.083871   train-mae:0.045876 
## [568]    eval-mae:0.083859   train-mae:0.045829 
## [569]    eval-mae:0.083843   train-mae:0.045788 
## [570]    eval-mae:0.083819   train-mae:0.045774 
## [571]    eval-mae:0.083869   train-mae:0.045727 
## [572]    eval-mae:0.083920   train-mae:0.045674 
## [573]    eval-mae:0.083919   train-mae:0.045650 
## [574]    eval-mae:0.083938   train-mae:0.045619 
## [575]    eval-mae:0.083917   train-mae:0.045581 
## [576]    eval-mae:0.083931   train-mae:0.045545 
## [577]    eval-mae:0.083879   train-mae:0.045508 
## [578]    eval-mae:0.083853   train-mae:0.045480 
## [579]    eval-mae:0.083834   train-mae:0.045453 
## [580]    eval-mae:0.083861   train-mae:0.045425 
## [581]    eval-mae:0.083882   train-mae:0.045386 
## [582]    eval-mae:0.083881   train-mae:0.045353 
## [583]    eval-mae:0.083884   train-mae:0.045307 
## [584]    eval-mae:0.083881   train-mae:0.045272 
## [585]    eval-mae:0.083879   train-mae:0.045234 
## [586]    eval-mae:0.083839   train-mae:0.045194 
## [587]    eval-mae:0.083812   train-mae:0.045156 
## [588]    eval-mae:0.083850   train-mae:0.045141 
## [589]    eval-mae:0.083856   train-mae:0.045110 
## [590]    eval-mae:0.083834   train-mae:0.045063 
## [591]    eval-mae:0.083821   train-mae:0.045037 
## [592]    eval-mae:0.083797   train-mae:0.044993 
## [593]    eval-mae:0.083789   train-mae:0.044946 
## [594]    eval-mae:0.083779   train-mae:0.044935 
## [595]    eval-mae:0.083772   train-mae:0.044895 
## [596]    eval-mae:0.083797   train-mae:0.044883 
## [597]    eval-mae:0.083818   train-mae:0.044855 
## [598]    eval-mae:0.083830   train-mae:0.044829 
## [599]    eval-mae:0.083813   train-mae:0.044787 
## [600]    eval-mae:0.083772   train-mae:0.044749 
## [601]    eval-mae:0.083758   train-mae:0.044721 
## [602]    eval-mae:0.083731   train-mae:0.044681 
## [603]    eval-mae:0.083759   train-mae:0.044630 
## [604]    eval-mae:0.083749   train-mae:0.044590 
## [605]    eval-mae:0.083722   train-mae:0.044564 
## [606]    eval-mae:0.083730   train-mae:0.044516 
## [607]    eval-mae:0.083769   train-mae:0.044474 
## [608]    eval-mae:0.083765   train-mae:0.044426 
## [609]    eval-mae:0.083755   train-mae:0.044395 
## [610]    eval-mae:0.083184   train-mae:0.044377 
## [611]    eval-mae:0.083125   train-mae:0.044355 
## [612]    eval-mae:0.083128   train-mae:0.044330 
## [613]    eval-mae:0.083133   train-mae:0.044309 
## [614]    eval-mae:0.083118   train-mae:0.044274 
## [615]    eval-mae:0.083122   train-mae:0.044259 
## [616]    eval-mae:0.083136   train-mae:0.044192 
## [617]    eval-mae:0.083122   train-mae:0.044152 
## [618]    eval-mae:0.083146   train-mae:0.044102 
## [619]    eval-mae:0.083129   train-mae:0.044062 
## [620]    eval-mae:0.083112   train-mae:0.044038 
## [621]    eval-mae:0.083128   train-mae:0.043983 
## [622]    eval-mae:0.083160   train-mae:0.043955 
## [623]    eval-mae:0.083160   train-mae:0.043931 
## [624]    eval-mae:0.083141   train-mae:0.043882 
## [625]    eval-mae:0.083063   train-mae:0.043845 
## [626]    eval-mae:0.083058   train-mae:0.043815 
## [627]    eval-mae:0.083066   train-mae:0.043773 
## [628]    eval-mae:0.082594   train-mae:0.043764 
## [629]    eval-mae:0.082608   train-mae:0.043735 
## [630]    eval-mae:0.082599   train-mae:0.043704 
## [631]    eval-mae:0.082554   train-mae:0.043646 
## [632]    eval-mae:0.082559   train-mae:0.043611 
## [633]    eval-mae:0.082571   train-mae:0.043567 
## [634]    eval-mae:0.082574   train-mae:0.043515 
## [635]    eval-mae:0.082560   train-mae:0.043513 
## [636]    eval-mae:0.082534   train-mae:0.043489 
## [637]    eval-mae:0.082546   train-mae:0.043475 
## [638]    eval-mae:0.082504   train-mae:0.043430 
## [639]    eval-mae:0.082500   train-mae:0.043392 
## [640]    eval-mae:0.082509   train-mae:0.043369 
## [641]    eval-mae:0.082480   train-mae:0.043328 
## [642]    eval-mae:0.082465   train-mae:0.043285 
## [643]    eval-mae:0.082479   train-mae:0.043252 
## [644]    eval-mae:0.082498   train-mae:0.043217 
## [645]    eval-mae:0.082482   train-mae:0.043201 
## [646]    eval-mae:0.082426   train-mae:0.043154 
## [647]    eval-mae:0.082397   train-mae:0.043114 
## [648]    eval-mae:0.082370   train-mae:0.043101 
## [649]    eval-mae:0.082360   train-mae:0.043095 
## [650]    eval-mae:0.082347   train-mae:0.043057 
## [651]    eval-mae:0.082353   train-mae:0.043026 
## [652]    eval-mae:0.082386   train-mae:0.042987 
## [653]    eval-mae:0.082540   train-mae:0.042955 
## [654]    eval-mae:0.082546   train-mae:0.042921 
## [655]    eval-mae:0.082538   train-mae:0.042910 
## [656]    eval-mae:0.082519   train-mae:0.042877 
## [657]    eval-mae:0.082486   train-mae:0.042846 
## [658]    eval-mae:0.082517   train-mae:0.042802 
## [659]    eval-mae:0.082529   train-mae:0.042793 
## [660]    eval-mae:0.082736   train-mae:0.042778 
## [661]    eval-mae:0.082703   train-mae:0.042731 
## [662]    eval-mae:0.082692   train-mae:0.042679 
## [663]    eval-mae:0.082664   train-mae:0.042631 
## [664]    eval-mae:0.082711   train-mae:0.042607 
## [665]    eval-mae:0.082700   train-mae:0.042594 
## [666]    eval-mae:0.082730   train-mae:0.042547 
## [667]    eval-mae:0.082709   train-mae:0.042515 
## [668]    eval-mae:0.082710   train-mae:0.042496 
## [669]    eval-mae:0.082713   train-mae:0.042460 
## [670]    eval-mae:0.082732   train-mae:0.042417 
## [671]    eval-mae:0.082707   train-mae:0.042398 
## [672]    eval-mae:0.082714   train-mae:0.042370 
## [673]    eval-mae:0.082732   train-mae:0.042333 
## [674]    eval-mae:0.082714   train-mae:0.042310 
## [675]    eval-mae:0.082727   train-mae:0.042288 
## [676]    eval-mae:0.082659   train-mae:0.042249 
## [677]    eval-mae:0.082657   train-mae:0.042231 
## [678]    eval-mae:0.082255   train-mae:0.042229 
## [679]    eval-mae:0.082245   train-mae:0.042204 
## [680]    eval-mae:0.082245   train-mae:0.042195 
## [681]    eval-mae:0.082193   train-mae:0.042151 
## [682]    eval-mae:0.082198   train-mae:0.042120 
## [683]    eval-mae:0.082191   train-mae:0.042080 
## [684]    eval-mae:0.082182   train-mae:0.042057 
## [685]    eval-mae:0.082129   train-mae:0.042027 
## [686]    eval-mae:0.082126   train-mae:0.042013 
## [687]    eval-mae:0.082111   train-mae:0.041975 
## [688]    eval-mae:0.082122   train-mae:0.041936 
## [689]    eval-mae:0.082117   train-mae:0.041894 
## [690]    eval-mae:0.082102   train-mae:0.041851 
## [691]    eval-mae:0.082152   train-mae:0.041832 
## [692]    eval-mae:0.082135   train-mae:0.041814 
## [693]    eval-mae:0.082112   train-mae:0.041762 
## [694]    eval-mae:0.082119   train-mae:0.041745 
## [695]    eval-mae:0.082079   train-mae:0.041697 
## [696]    eval-mae:0.082064   train-mae:0.041669 
## [697]    eval-mae:0.082041   train-mae:0.041626 
## [698]    eval-mae:0.082023   train-mae:0.041618 
## [699]    eval-mae:0.081983   train-mae:0.041580 
## [700]    eval-mae:0.081974   train-mae:0.041536 
## [701]    eval-mae:0.082011   train-mae:0.041498 
## [702]    eval-mae:0.081995   train-mae:0.041478 
## [703]    eval-mae:0.082008   train-mae:0.041446 
## [704]    eval-mae:0.082004   train-mae:0.041407 
## [705]    eval-mae:0.081988   train-mae:0.041385 
## [706]    eval-mae:0.082060   train-mae:0.041361 
## [707]    eval-mae:0.082040   train-mae:0.041329 
## [708]    eval-mae:0.082032   train-mae:0.041314 
## [709]    eval-mae:0.082054   train-mae:0.041304 
## [710]    eval-mae:0.082058   train-mae:0.041294 
## [711]    eval-mae:0.082060   train-mae:0.041238 
## [712]    eval-mae:0.082092   train-mae:0.041209 
## [713]    eval-mae:0.082079   train-mae:0.041165 
## [714]    eval-mae:0.082047   train-mae:0.041141 
## [715]    eval-mae:0.082048   train-mae:0.041120 
## [716]    eval-mae:0.082037   train-mae:0.041067 
## [717]    eval-mae:0.082029   train-mae:0.041033 
## [718]    eval-mae:0.082039   train-mae:0.041027 
## [719]    eval-mae:0.082013   train-mae:0.040986 
## [720]    eval-mae:0.082002   train-mae:0.040944 
## [721]    eval-mae:0.081925   train-mae:0.040908 
## [722]    eval-mae:0.081925   train-mae:0.040875 
## [723]    eval-mae:0.081958   train-mae:0.040859 
## [724]    eval-mae:0.081934   train-mae:0.040849 
## [725]    eval-mae:0.081981   train-mae:0.040810 
## [726]    eval-mae:0.081994   train-mae:0.040791 
## [727]    eval-mae:0.082016   train-mae:0.040765 
## [728]    eval-mae:0.082013   train-mae:0.040733 
## [729]    eval-mae:0.081985   train-mae:0.040709 
## [730]    eval-mae:0.081995   train-mae:0.040694 
## [731]    eval-mae:0.081950   train-mae:0.040663 
## [732]    eval-mae:0.081951   train-mae:0.040627 
## [733]    eval-mae:0.081946   train-mae:0.040607 
## [734]    eval-mae:0.081970   train-mae:0.040578 
## [735]    eval-mae:0.081972   train-mae:0.040551 
## [736]    eval-mae:0.081967   train-mae:0.040527 
## [737]    eval-mae:0.081953   train-mae:0.040493 
## [738]    eval-mae:0.081934   train-mae:0.040466 
## [739]    eval-mae:0.081940   train-mae:0.040443 
## [740]    eval-mae:0.081721   train-mae:0.040430 
## [741]    eval-mae:0.081709   train-mae:0.040379 
## [742]    eval-mae:0.081655   train-mae:0.040355 
## [743]    eval-mae:0.081632   train-mae:0.040331 
## [744]    eval-mae:0.081617   train-mae:0.040299 
## [745]    eval-mae:0.081620   train-mae:0.040286 
## [746]    eval-mae:0.081607   train-mae:0.040255 
## [747]    eval-mae:0.081590   train-mae:0.040207 
## [748]    eval-mae:0.081606   train-mae:0.040176 
## [749]    eval-mae:0.081599   train-mae:0.040151 
## [750]    eval-mae:0.081551   train-mae:0.040120 
## [751]    eval-mae:0.081543   train-mae:0.040106 
## [752]    eval-mae:0.081548   train-mae:0.040084 
## [753]    eval-mae:0.081553   train-mae:0.040057 
## [754]    eval-mae:0.081546   train-mae:0.040025 
## [755]    eval-mae:0.081541   train-mae:0.040000 
## [756]    eval-mae:0.081525   train-mae:0.039966 
## [757]    eval-mae:0.081550   train-mae:0.039926 
## [758]    eval-mae:0.081532   train-mae:0.039901 
## [759]    eval-mae:0.081501   train-mae:0.039869 
## [760]    eval-mae:0.081517   train-mae:0.039809 
## [761]    eval-mae:0.081492   train-mae:0.039765 
## [762]    eval-mae:0.081460   train-mae:0.039740 
## [763]    eval-mae:0.081411   train-mae:0.039709 
## [764]    eval-mae:0.081407   train-mae:0.039686 
## [765]    eval-mae:0.081346   train-mae:0.039653 
## [766]    eval-mae:0.081360   train-mae:0.039632 
## [767]    eval-mae:0.081332   train-mae:0.039603 
## [768]    eval-mae:0.081325   train-mae:0.039587 
## [769]    eval-mae:0.081310   train-mae:0.039555 
## [770]    eval-mae:0.081299   train-mae:0.039524 
## [771]    eval-mae:0.081338   train-mae:0.039502 
## [772]    eval-mae:0.081322   train-mae:0.039479 
## [773]    eval-mae:0.081322   train-mae:0.039471 
## [774]    eval-mae:0.081343   train-mae:0.039420 
## [775]    eval-mae:0.081323   train-mae:0.039392 
## [776]    eval-mae:0.081451   train-mae:0.039358 
## [777]    eval-mae:0.081454   train-mae:0.039340 
## [778]    eval-mae:0.081474   train-mae:0.039315 
## [779]    eval-mae:0.081465   train-mae:0.039286 
## [780]    eval-mae:0.081457   train-mae:0.039251 
## [781]    eval-mae:0.081455   train-mae:0.039237 
## [782]    eval-mae:0.081433   train-mae:0.039222 
## [783]    eval-mae:0.081434   train-mae:0.039198 
## [784]    eval-mae:0.081321   train-mae:0.039180 
## [785]    eval-mae:0.081348   train-mae:0.039128 
## [786]    eval-mae:0.081348   train-mae:0.039094 
## [787]    eval-mae:0.081357   train-mae:0.039076 
## [788]    eval-mae:0.081360   train-mae:0.039037 
## [789]    eval-mae:0.081355   train-mae:0.039030 
## [790]    eval-mae:0.081338   train-mae:0.038997 
## [791]    eval-mae:0.081296   train-mae:0.038952 
## [792]    eval-mae:0.081285   train-mae:0.038913 
## [793]    eval-mae:0.081278   train-mae:0.038890 
## [794]    eval-mae:0.081243   train-mae:0.038857 
## [795]    eval-mae:0.081208   train-mae:0.038838 
## [796]    eval-mae:0.081219   train-mae:0.038809 
## [797]    eval-mae:0.081215   train-mae:0.038795 
## [798]    eval-mae:0.081219   train-mae:0.038766 
## [799]    eval-mae:0.081235   train-mae:0.038741 
## [800]    eval-mae:0.081238   train-mae:0.038708 
## [801]    eval-mae:0.081194   train-mae:0.038675 
## [802]    eval-mae:0.081198   train-mae:0.038649 
## [803]    eval-mae:0.081176   train-mae:0.038638 
## [804]    eval-mae:0.081195   train-mae:0.038616 
## [805]    eval-mae:0.081199   train-mae:0.038605 
## [806]    eval-mae:0.081239   train-mae:0.038563 
## [807]    eval-mae:0.081191   train-mae:0.038522 
## [808]    eval-mae:0.081174   train-mae:0.038497 
## [809]    eval-mae:0.081168   train-mae:0.038456 
## [810]    eval-mae:0.081173   train-mae:0.038423 
## [811]    eval-mae:0.081171   train-mae:0.038400 
## [812]    eval-mae:0.081180   train-mae:0.038372 
## [813]    eval-mae:0.081186   train-mae:0.038345 
## [814]    eval-mae:0.081191   train-mae:0.038308 
## [815]    eval-mae:0.081176   train-mae:0.038267 
## [816]    eval-mae:0.081134   train-mae:0.038246 
## [817]    eval-mae:0.081134   train-mae:0.038245 
## [818]    eval-mae:0.081116   train-mae:0.038208 
## [819]    eval-mae:0.081122   train-mae:0.038193 
## [820]    eval-mae:0.081122   train-mae:0.038181 
## [821]    eval-mae:0.081108   train-mae:0.038160 
## [822]    eval-mae:0.081066   train-mae:0.038127 
## [823]    eval-mae:0.081006   train-mae:0.038104 
## [824]    eval-mae:0.080996   train-mae:0.038099 
## [825]    eval-mae:0.080992   train-mae:0.038055 
## [826]    eval-mae:0.081000   train-mae:0.038045 
## [827]    eval-mae:0.081026   train-mae:0.038005 
## [828]    eval-mae:0.081042   train-mae:0.037976 
## [829]    eval-mae:0.081048   train-mae:0.037961 
## [830]    eval-mae:0.081036   train-mae:0.037942 
## [831]    eval-mae:0.081047   train-mae:0.037905 
## [832]    eval-mae:0.081007   train-mae:0.037888 
## [833]    eval-mae:0.081037   train-mae:0.037862 
## [834]    eval-mae:0.081004   train-mae:0.037845 
## [835]    eval-mae:0.081014   train-mae:0.037795 
## [836]    eval-mae:0.080995   train-mae:0.037767 
## [837]    eval-mae:0.080989   train-mae:0.037734 
## [838]    eval-mae:0.080951   train-mae:0.037716 
## [839]    eval-mae:0.080926   train-mae:0.037657 
## [840]    eval-mae:0.080914   train-mae:0.037630 
## [841]    eval-mae:0.080921   train-mae:0.037595 
## [842]    eval-mae:0.080914   train-mae:0.037580 
## [843]    eval-mae:0.080885   train-mae:0.037561 
## [844]    eval-mae:0.080898   train-mae:0.037552 
## [845]    eval-mae:0.080906   train-mae:0.037534 
## [846]    eval-mae:0.080894   train-mae:0.037504 
## [847]    eval-mae:0.080900   train-mae:0.037472 
## [848]    eval-mae:0.080901   train-mae:0.037456 
## [849]    eval-mae:0.080900   train-mae:0.037432 
## [850]    eval-mae:0.080889   train-mae:0.037425 
## [851]    eval-mae:0.080876   train-mae:0.037384 
## [852]    eval-mae:0.080868   train-mae:0.037361 
## [853]    eval-mae:0.080866   train-mae:0.037343 
## [854]    eval-mae:0.080818   train-mae:0.037305 
## [855]    eval-mae:0.080843   train-mae:0.037285 
## [856]    eval-mae:0.080827   train-mae:0.037247 
## [857]    eval-mae:0.080838   train-mae:0.037215 
## [858]    eval-mae:0.080844   train-mae:0.037182 
## [859]    eval-mae:0.080832   train-mae:0.037158 
## [860]    eval-mae:0.080888   train-mae:0.037131 
## [861]    eval-mae:0.080927   train-mae:0.037107 
## [862]    eval-mae:0.080920   train-mae:0.037061 
## [863]    eval-mae:0.080911   train-mae:0.037031 
## [864]    eval-mae:0.080905   train-mae:0.036995 
## [865]    eval-mae:0.080919   train-mae:0.036978 
## [866]    eval-mae:0.080915   train-mae:0.036956 
## [867]    eval-mae:0.080922   train-mae:0.036923 
## [868]    eval-mae:0.080952   train-mae:0.036889 
## [869]    eval-mae:0.080953   train-mae:0.036857 
## [870]    eval-mae:0.080890   train-mae:0.036809 
## [871]    eval-mae:0.080880   train-mae:0.036796 
## [872]    eval-mae:0.080865   train-mae:0.036770 
## [873]    eval-mae:0.080851   train-mae:0.036742 
## [874]    eval-mae:0.080848   train-mae:0.036699 
## [875]    eval-mae:0.080831   train-mae:0.036693 
## [876]    eval-mae:0.080819   train-mae:0.036662 
## [877]    eval-mae:0.080816   train-mae:0.036639 
## [878]    eval-mae:0.080817   train-mae:0.036610 
## [879]    eval-mae:0.080853   train-mae:0.036578 
## [880]    eval-mae:0.080859   train-mae:0.036565 
## [881]    eval-mae:0.080858   train-mae:0.036533 
## [882]    eval-mae:0.080855   train-mae:0.036494 
## [883]    eval-mae:0.080840   train-mae:0.036474 
## [884]    eval-mae:0.080839   train-mae:0.036462 
## [885]    eval-mae:0.080828   train-mae:0.036437 
## [886]    eval-mae:0.080783   train-mae:0.036398 
## [887]    eval-mae:0.080783   train-mae:0.036363 
## [888]    eval-mae:0.080781   train-mae:0.036339 
## [889]    eval-mae:0.080789   train-mae:0.036333 
## [890]    eval-mae:0.080756   train-mae:0.036293 
## [891]    eval-mae:0.080767   train-mae:0.036256 
## [892]    eval-mae:0.080778   train-mae:0.036230 
## [893]    eval-mae:0.080791   train-mae:0.036200 
## [894]    eval-mae:0.080790   train-mae:0.036175 
## [895]    eval-mae:0.080790   train-mae:0.036152 
## [896]    eval-mae:0.080791   train-mae:0.036121 
## [897]    eval-mae:0.080788   train-mae:0.036099 
## [898]    eval-mae:0.080779   train-mae:0.036068 
## [899]    eval-mae:0.080804   train-mae:0.036035 
## [900]    eval-mae:0.080797   train-mae:0.036011 
## [901]    eval-mae:0.080786   train-mae:0.035976 
## [902]    eval-mae:0.080790   train-mae:0.035943 
## [903]    eval-mae:0.080781   train-mae:0.035902 
## [904]    eval-mae:0.080767   train-mae:0.035876 
## [905]    eval-mae:0.080753   train-mae:0.035863 
## [906]    eval-mae:0.080769   train-mae:0.035848 
## [907]    eval-mae:0.080891   train-mae:0.035827 
## [908]    eval-mae:0.080911   train-mae:0.035775 
## [909]    eval-mae:0.080912   train-mae:0.035729 
## [910]    eval-mae:0.080923   train-mae:0.035712 
## [911]    eval-mae:0.080928   train-mae:0.035680 
## [912]    eval-mae:0.080901   train-mae:0.035669 
## [913]    eval-mae:0.080920   train-mae:0.035649 
## [914]    eval-mae:0.080902   train-mae:0.035630 
## [915]    eval-mae:0.080925   train-mae:0.035594 
## [916]    eval-mae:0.080898   train-mae:0.035575 
## [917]    eval-mae:0.080903   train-mae:0.035552 
## [918]    eval-mae:0.081019   train-mae:0.035543 
## [919]    eval-mae:0.081006   train-mae:0.035508 
## [920]    eval-mae:0.081035   train-mae:0.035461 
## [921]    eval-mae:0.081015   train-mae:0.035436 
## [922]    eval-mae:0.081013   train-mae:0.035406 
## [923]    eval-mae:0.080998   train-mae:0.035371 
## [924]    eval-mae:0.080992   train-mae:0.035346 
## [925]    eval-mae:0.080968   train-mae:0.035323 
## [926]    eval-mae:0.080941   train-mae:0.035300 
## [927]    eval-mae:0.080940   train-mae:0.035269 
## [928]    eval-mae:0.080921   train-mae:0.035256 
## [929]    eval-mae:0.080920   train-mae:0.035243 
## [930]    eval-mae:0.080942   train-mae:0.035210 
## [931]    eval-mae:0.080951   train-mae:0.035189 
## [932]    eval-mae:0.080991   train-mae:0.035158 
## [933]    eval-mae:0.080865   train-mae:0.035144 
## [934]    eval-mae:0.080879   train-mae:0.035121 
## [935]    eval-mae:0.080883   train-mae:0.035085 
## [936]    eval-mae:0.080880   train-mae:0.035056 
## [937]    eval-mae:0.080885   train-mae:0.035024 
## [938]    eval-mae:0.080903   train-mae:0.034991 
## [939]    eval-mae:0.080995   train-mae:0.034968 
## [940]    eval-mae:0.081014   train-mae:0.034942 
## [941]    eval-mae:0.081009   train-mae:0.034920 
## [942]    eval-mae:0.081000   train-mae:0.034892 
## [943]    eval-mae:0.080989   train-mae:0.034861 
## [944]    eval-mae:0.081009   train-mae:0.034863 
## [945]    eval-mae:0.081009   train-mae:0.034845 
## [946]    eval-mae:0.080985   train-mae:0.034808 
## [947]    eval-mae:0.080977   train-mae:0.034772 
## [948]    eval-mae:0.081004   train-mae:0.034745 
## [949]    eval-mae:0.080999   train-mae:0.034696 
## [950]    eval-mae:0.081015   train-mae:0.034681 
## [951]    eval-mae:0.081012   train-mae:0.034649 
## [952]    eval-mae:0.081019   train-mae:0.034635 
## [953]    eval-mae:0.081019   train-mae:0.034628 
## [954]    eval-mae:0.081012   train-mae:0.034602 
## [955]    eval-mae:0.081014   train-mae:0.034561 
## [956]    eval-mae:0.081027   train-mae:0.034521 
## [957]    eval-mae:0.081019   train-mae:0.034492 
## [958]    eval-mae:0.081032   train-mae:0.034465 
## [959]    eval-mae:0.081021   train-mae:0.034441 
## [960]    eval-mae:0.081023   train-mae:0.034426 
## [961]    eval-mae:0.081008   train-mae:0.034410 
## [962]    eval-mae:0.081013   train-mae:0.034393 
## [963]    eval-mae:0.081018   train-mae:0.034386 
## [964]    eval-mae:0.081015   train-mae:0.034352 
## [965]    eval-mae:0.080996   train-mae:0.034339 
## [966]    eval-mae:0.081023   train-mae:0.034321 
## [967]    eval-mae:0.081046   train-mae:0.034300 
## [968]    eval-mae:0.081037   train-mae:0.034290 
## [969]    eval-mae:0.081045   train-mae:0.034268 
## [970]    eval-mae:0.081048   train-mae:0.034238 
## [971]    eval-mae:0.081015   train-mae:0.034224 
## [972]    eval-mae:0.081020   train-mae:0.034200 
## [973]    eval-mae:0.081022   train-mae:0.034190 
## [974]    eval-mae:0.081010   train-mae:0.034161 
## [975]    eval-mae:0.081000   train-mae:0.034127 
## [976]    eval-mae:0.080990   train-mae:0.034102 
## [977]    eval-mae:0.080977   train-mae:0.034080 
## [978]    eval-mae:0.080960   train-mae:0.034067 
## [979]    eval-mae:0.080949   train-mae:0.034053 
## [980]    eval-mae:0.080940   train-mae:0.034017 
## [981]    eval-mae:0.080915   train-mae:0.033997 
## [982]    eval-mae:0.080893   train-mae:0.033971 
## [983]    eval-mae:0.080912   train-mae:0.033962 
## [984]    eval-mae:0.080910   train-mae:0.033948 
## [985]    eval-mae:0.080915   train-mae:0.033927 
## [986]    eval-mae:0.080915   train-mae:0.033923 
## [987]    eval-mae:0.080909   train-mae:0.033910 
## [988]    eval-mae:0.080936   train-mae:0.033896 
## [989]    eval-mae:0.080937   train-mae:0.033895 
## [990]    eval-mae:0.080934   train-mae:0.033880 
## [991]    eval-mae:0.080933   train-mae:0.033856 
## [992]    eval-mae:0.080948   train-mae:0.033830 
## [993]    eval-mae:0.080964   train-mae:0.033823 
## [994]    eval-mae:0.080979   train-mae:0.033783 
## [995]    eval-mae:0.080932   train-mae:0.033746 
## [996]    eval-mae:0.080966   train-mae:0.033725 
## [997]    eval-mae:0.080970   train-mae:0.033710 
## [998]    eval-mae:0.080980   train-mae:0.033682 
## [999]    eval-mae:0.080963   train-mae:0.033658 
## [1000]   eval-mae:0.080967   train-mae:0.033639

eval <- bst$evaluation_log %>% gather(tipo, rmse, -iter)
ggplot(eval, aes(x=iter, y=rmse, colour=tipo, group= tipo)) + geom_line() +
  scale_y_log10()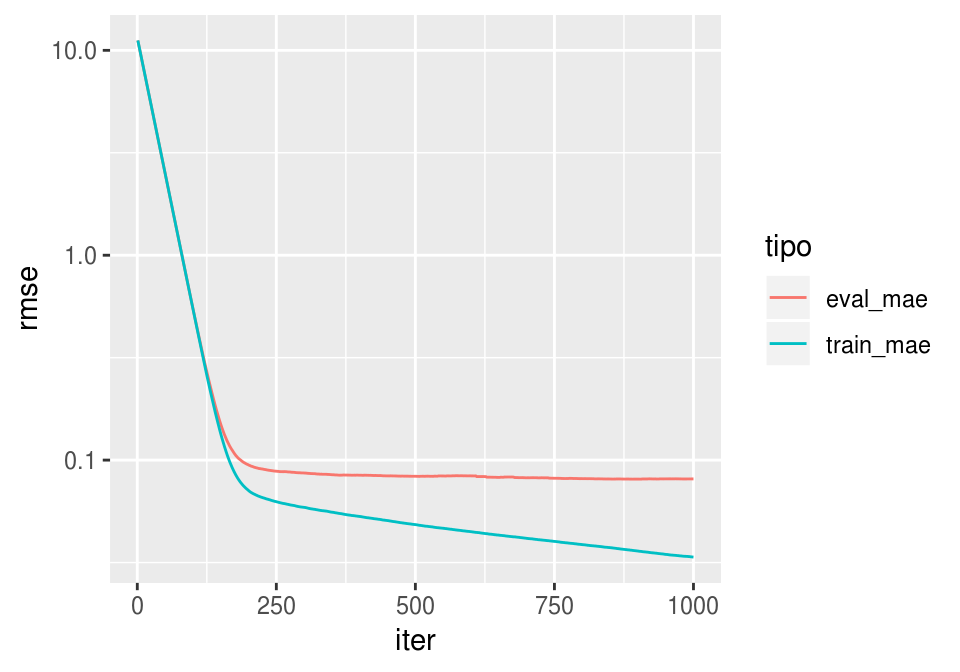

References

Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2017. The Elements of Statistical Learning. Springer Series in Statistics. Springer New York Inc. http://web.stanford.edu/~hastie/ElemStatLearn/.