12  Aplicaciones de modelos de espacio de estados

Código 
library(tidyverse)
library(kableExtra)
library(DiagrammeR)
library(CausalImpact)
locale <- Sys.setlocale("LC_TIME", "es_ES.UTF-8")
library(lubridate)
library(tsibble)
library(feasts)
ggplot2::theme_set(ggplot2::theme_light())

12.1 Pronósticos

Consideramos un ejemplo de Hyndman y Athanasopoulos (2014) en la esta sección, donde buscamos hacer pronósticos de empleo en Estados Unidos. Consideramos los datos de entretenimiento y hospitalidad:

load("../datos/us_employment.rda")
ent_hosp_tbl <- filter(us_employment, 
  Title == "Leisure and Hospitality") |> 
  filter_index("2000-01" ~ . )
ent_hosp_ts <- ent_hosp_tbl |> as.ts(Employed)
#ent_hosp_ts <- log(ent_hosp_ts)
autoplot(ent_hosp_tbl, Employed)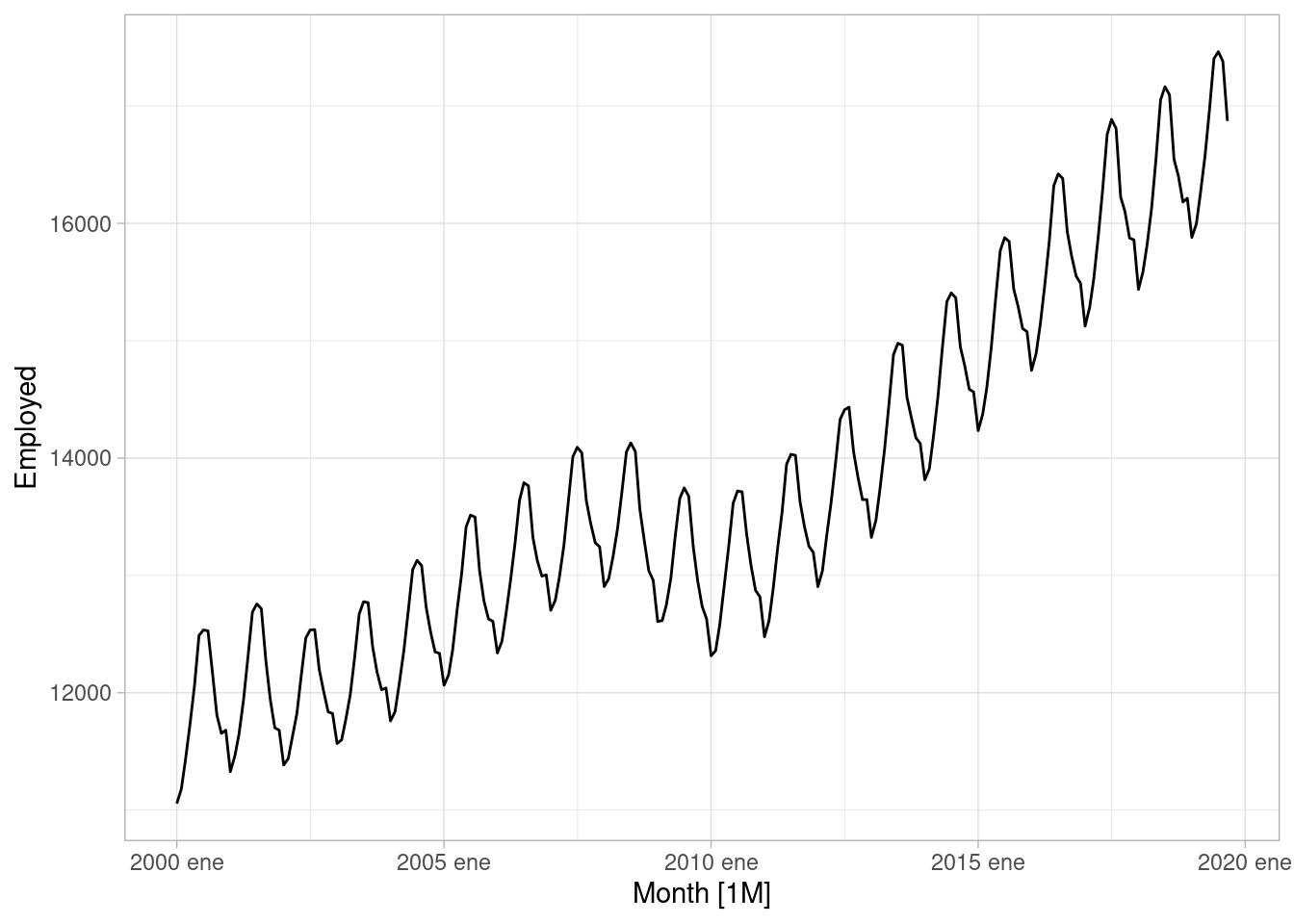

Intentaremos usar varios modelos, incluso algunos que claramente no son correctos:

  1. Nivel local
  2. Nivel local y tendencia
  3. Nivel local con estacionalidad (12 meses)
  4. Nivel local con tendencia y estacionalidad (12 meses)
  5. Nivel semilocal con tendencia y estacionalidad
  6. Nivel semilocal con tendencia, estacionalidad, y una componente autoregresiva.

En este ejemplo usaremos el paquete bsts que implementa modelos de espacio de estados usuales de manera relativamente fácil y rápida (aunque es necesario hacer diagnósticos aparte), y tiene algunas funciones convenientes para evaluar pronósticos.

library(bsts)
set.seed(998)
#inicial_nivel <- NormalPrior(11000, 1500, initial.value = 11000)
mod_spec_1 <- AddLocalLevel(list(), y = ent_hosp_ts)
mod_spec_2 <- AddLocalLinearTrend(list(), y = ent_hosp_ts)
mod_spec_3 <- AddLocalLevel(list(), y = ent_hosp_ts) |> 
  AddSeasonal(nseasons = 12, y = ent_hosp_ts)
mod_spec_4 <- AddLocalLinearTrend(list(), y = ent_hosp_ts) |> 
  AddSeasonal(nseasons = 12, y = ent_hosp_ts) 
mod_spec_5 <- AddSemilocalLinearTrend(list(), y = ent_hosp_ts) |> 
  AddSeasonal(nseasons = 12, y = ent_hosp_ts) 
mod_spec_6 <- AddSemilocalLinearTrend(list(), y = ent_hosp_ts) |> 
  AddSeasonal(nseasons = 12, y = ent_hosp_ts) |> 
  AddAr(lags = 2, y = ent_hosp_ts)
specs <- list(mod_spec_1, mod_spec_2, mod_spec_3, mod_spec_4, mod_spec_5, mod_spec_6)
ajustes <- map(specs, function(spec){
  bsts(ent_hosp_ts, spec, niter = 40000, ping = 10000)
})
=-=-=-=-= Iteration 0 Wed May 15 13:32:59 2024 =-=-=-=-=
=-=-=-=-= Iteration 10000 Wed May 15 13:33:08 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Wed May 15 13:33:18 2024 =-=-=-=-=
=-=-=-=-= Iteration 30000 Wed May 15 13:33:27 2024 =-=-=-=-=
=-=-=-=-= Iteration 0 Wed May 15 13:33:36 2024 =-=-=-=-=
=-=-=-=-= Iteration 10000 Wed May 15 13:33:48 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Wed May 15 13:33:59 2024 =-=-=-=-=
=-=-=-=-= Iteration 30000 Wed May 15 13:34:11 2024 =-=-=-=-=
=-=-=-=-= Iteration 0 Wed May 15 13:34:22 2024 =-=-=-=-=
=-=-=-=-= Iteration 10000 Wed May 15 13:34:48 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Wed May 15 13:35:14 2024 =-=-=-=-=
=-=-=-=-= Iteration 30000 Wed May 15 13:35:40 2024 =-=-=-=-=
=-=-=-=-= Iteration 0 Wed May 15 13:36:06 2024 =-=-=-=-=
=-=-=-=-= Iteration 10000 Wed May 15 13:36:38 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Wed May 15 13:37:10 2024 =-=-=-=-=
=-=-=-=-= Iteration 30000 Wed May 15 13:37:42 2024 =-=-=-=-=
=-=-=-=-= Iteration 0 Wed May 15 13:38:14 2024 =-=-=-=-=
=-=-=-=-= Iteration 10000 Wed May 15 13:38:47 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Wed May 15 13:39:19 2024 =-=-=-=-=
=-=-=-=-= Iteration 30000 Wed May 15 13:39:51 2024 =-=-=-=-=
=-=-=-=-= Iteration 0 Wed May 15 13:40:23 2024 =-=-=-=-=
=-=-=-=-= Iteration 10000 Wed May 15 13:41:08 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Wed May 15 13:41:54 2024 =-=-=-=-=
=-=-=-=-= Iteration 30000 Wed May 15 13:42:39 2024 =-=-=-=-=

En primer lugar, podemos comparar las predicciones a un paso de cada modelo. En este caso, los modelos 3 y 4 son claramente superiores a 1 y 2 en desempeño a un paso. El mejor modelo en desempeño a un paso es el modelo 4, por la tendencia lineal de la serie.

CompareBstsModels(ajustes, burn = 20000)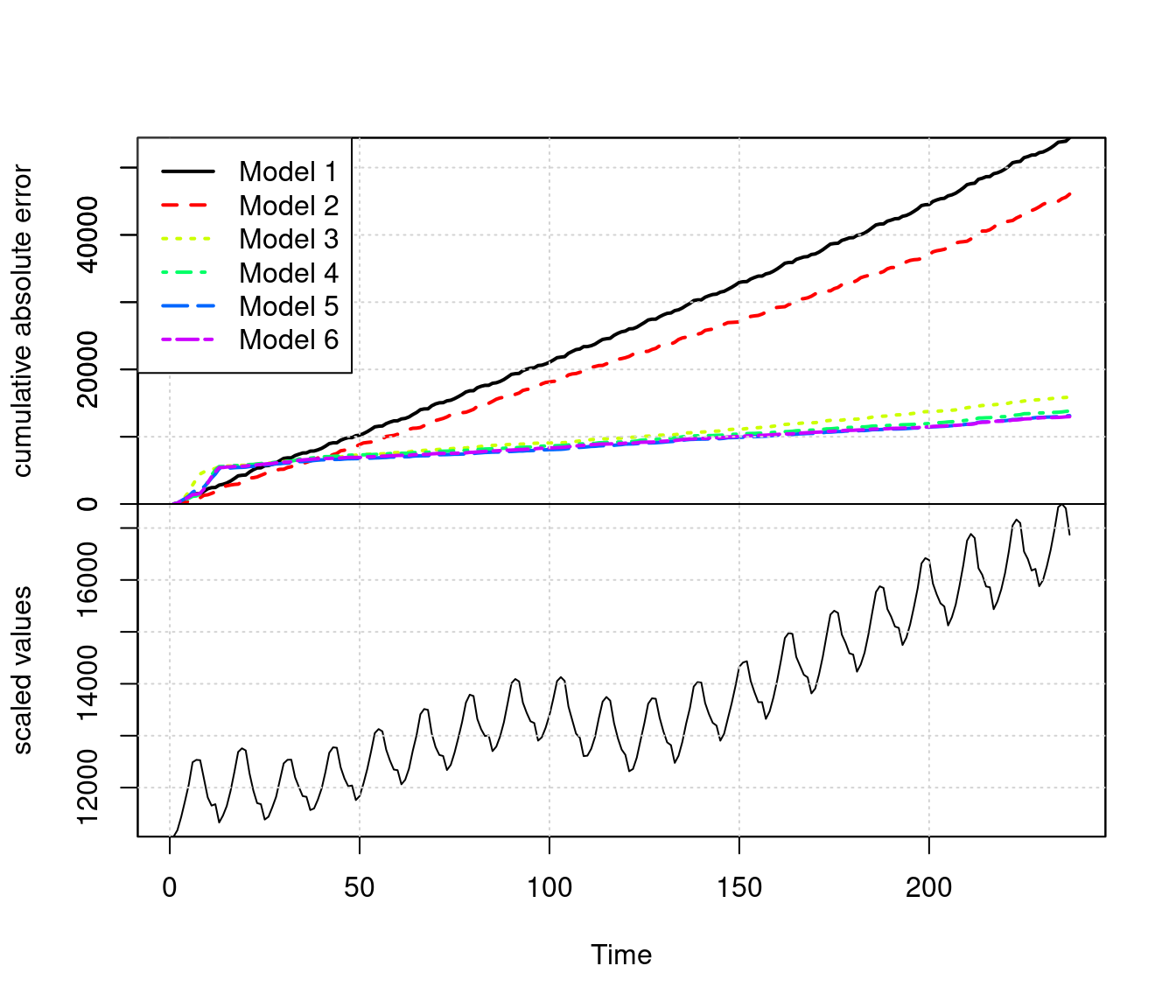

ajuste <- ajustes[[6]]
plot(ajuste, "components")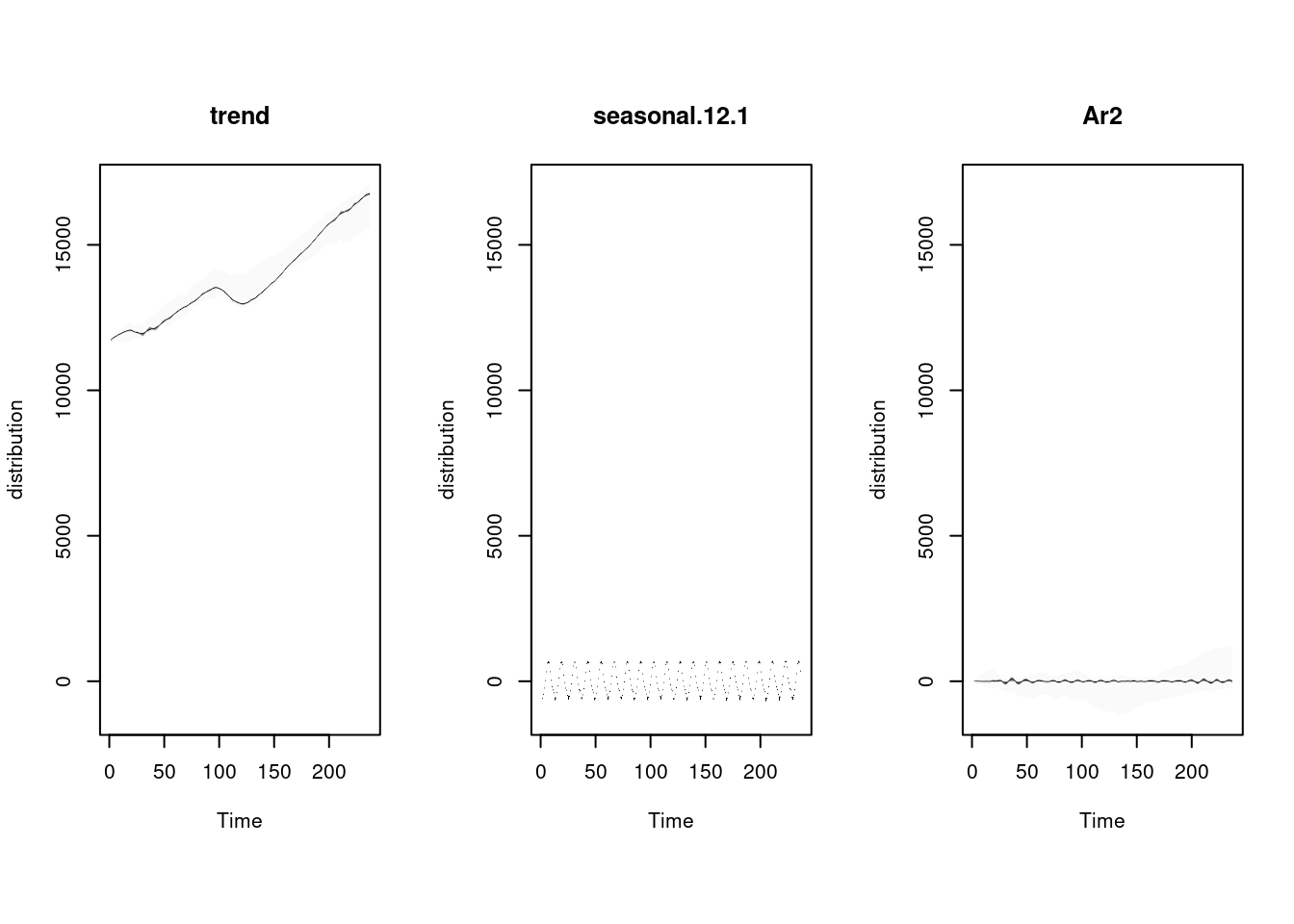

pred_errors_tbl <- 
  bsts.prediction.errors(ajuste, burn = 20000)$in.sample |> 
  t() |> as_tibble() |>
  mutate(t = 1: length(ent_hosp_ts)) |> 
  pivot_longer(-c(t), names_to = "sim", values_to = "valor") |>
  group_by(t) |> 
  summarise(valor = mean(valor)) |> 
  as_tsibble(index = t)
Warning: The `x` argument of `as_tibble.matrix()` must have unique column names if
`.name_repair` is omitted as of tibble 2.0.0.
ℹ Using compatibility `.name_repair`.
# filtramos a partir de 12 meses (mínimo requerido para
# estimar estacionalidad):
ACF(pred_errors_tbl |> filter(t > 12), valor, lag_max = 20) |> 
  autoplot() + ylim(c(-1,1))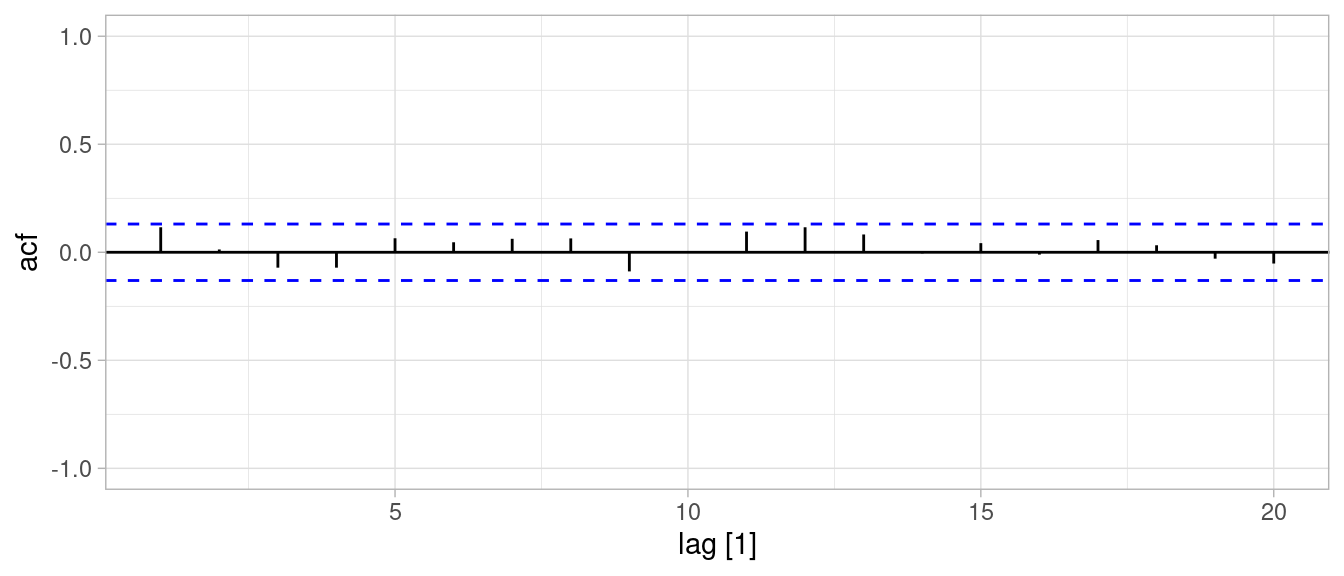

Ahora podemos hacer pronósticos:

ajuste <- ajustes[[6]]
pred <- predict(ajuste, horizon = 36, burn = 30000)
  plot(pred)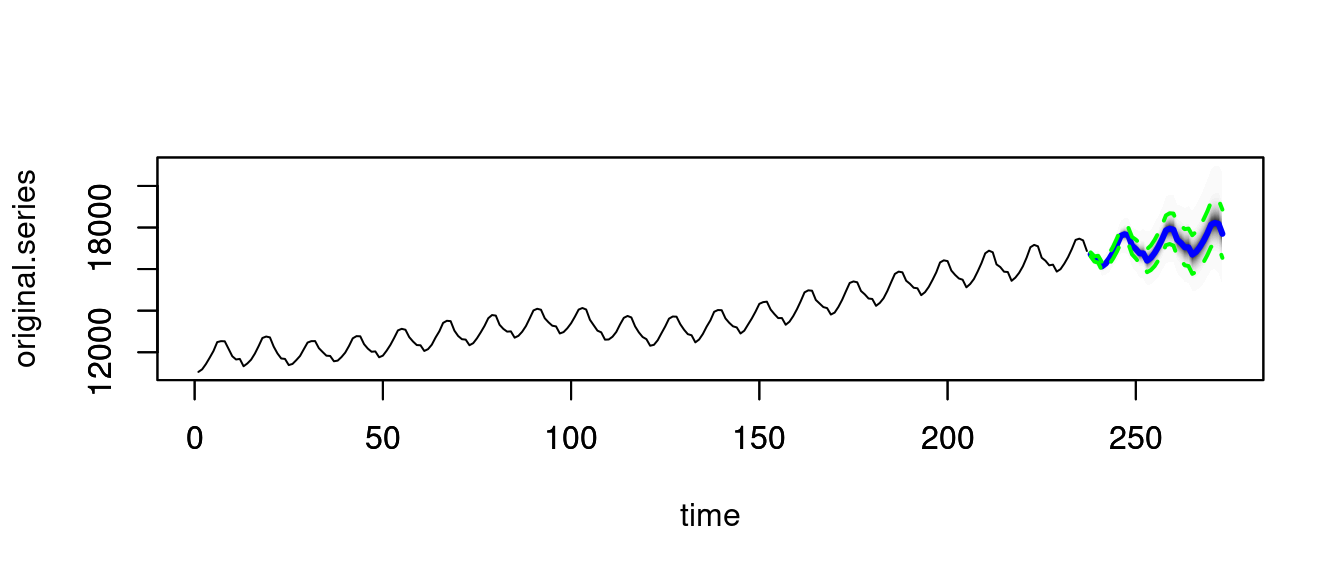

Podemos hacer también pronósticos agregados. Como tenemos simulaciones de los pronósticos, esto es fácil, incluyendo intervalos predictivos. En el siguiente ejemplo, hacemos un intervalo para la suma de los 36 meses que pronosticamos:

pred$distribution |> dim()
[1] 10000    36
apply(pred$distribution, 1, sum) |> qplot()
Warning: `qplot()` was deprecated in ggplot2 3.4.0.
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.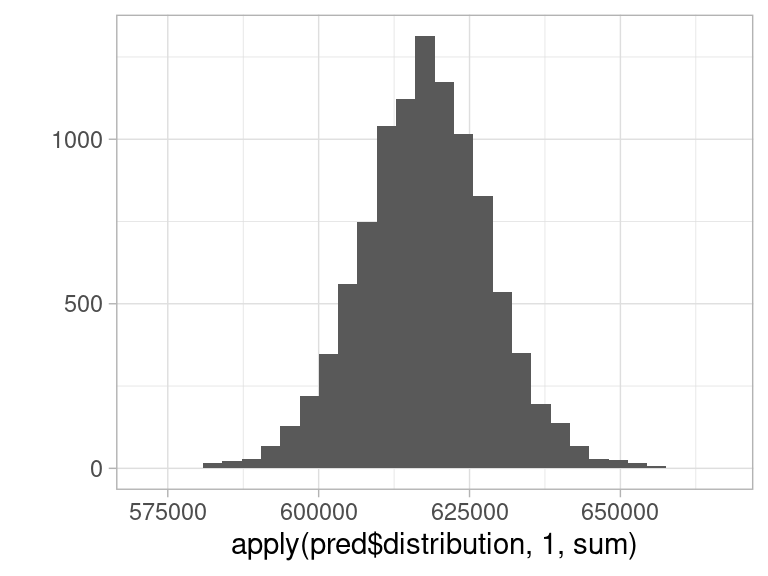

print("Intervalo de 90% para el agregado:")
[1] "Intervalo de 90% para el agregado:"
apply(pred$distribution, 1, sum) |> quantile(c(0.05, 0.50, 0.95))
      5%      50%      95% 
600267.7 617692.1 635036.2

12.2 Análisis de datos diarios

Consideremos por ejemplo la siguiente serie de nacimientos por día en México (ver la sección de introducción de series de tiempo):

natalidad_tbl <- read_rds("../datos/natalidad.rds") |> 
  ungroup() |> 
  arrange(fecha) |> 
  filter(fecha >= ymd("2008-01-01")) |> 
  mutate(nacimientos = log(n)) |> 
  select(-fecha_str, -n) |> 
  as_tsibble(index = fecha)
y <- natalidad_tbl |> as.ts(frequency = 365.25)
y <- zoo(natalidad_tbl$nacimientos, natalidad_tbl$fecha)
natalidad_tbl <- natalidad_tbl |> 
  mutate(feb_29 = as.numeric(month(fecha)==2 & day(fecha) == 29))
feb_29 <- natalidad_tbl$feb_29
mar_1_feb_29 <- lag(feb_29, default = 0)

En este caso, es necesario:

  • Agregar estacionalidad con periodo de 7 días
  • Agregar estacionalidad con periodo de 1 año
  • Agregar efectos de días de asueto, incluyendo posibles efectos que no ocurren solamente el día en cuestión, sino en los “hombros” del día (unos días antes o después).

La estacionalidad anual la modelamos con armónicos de periodo 365.25, es decir, con \(\lambda_j = 2\pi j /365.25\). Cada armónico agrega dos coeficientes al espacio de estados.

Estacionalidad trigonométrica

Supongamos que queremos modelar estacionalidad anual para datos mensuales usando armónicos. El primer armónico tiene un ciclo de 12 meses, así que ponemos \[\lambda_1 = 2\pi /12 = \pi/6\] Consideramos las funciones

\[f_1(t) = a\cos(\lambda_1 t) + b \sin(\lambda_1 t)\]

Con el tamaño de a y b se define la amplitud, y la fase depende de los tamaños relativos de \(a\) y \(b\). Esto lo podemos ver, por ejemplo, notando que \(a\sin x + b\cos x = \sqrt{a^2 + b^2}\sin(x + \alpha)\).

arm_1 <- tibble(t=1:25) |> 
  mutate(f_1 = -2 * cos(t * pi / 6) + 4 * sin(t * pi / 6)) |> 
  mutate(n = 1) |> 
bind_rows(
  tibble(t=1:25) |> 
  mutate(f_1 = 0.5 * cos(t * pi / 6) + 0.1 * sin(t * pi / 6)) |> 
  mutate(n = 2)
) 
ggplot(arm_1, aes(x = t, y = f_1, colour = factor(n))) + geom_line() + 
  geom_point() +
  geom_vline(xintercept = c(1, 13, 25))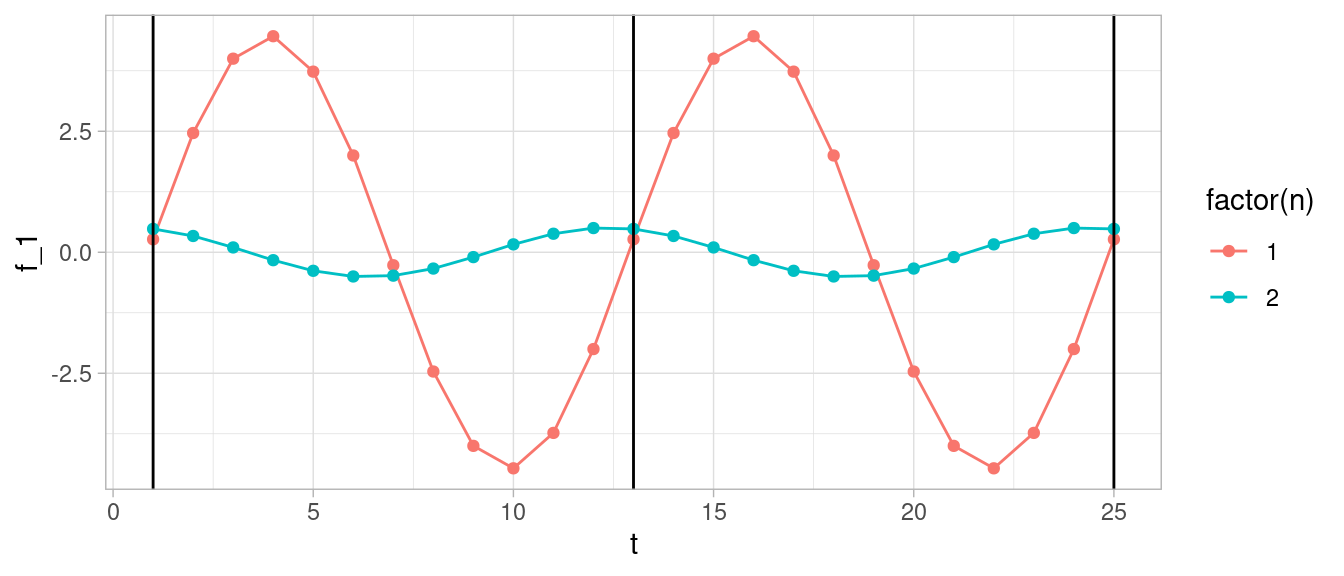

Podemos considerar armónicos más altos. El siguiente es

\[f_2(t) = f_1(t) + a_2\cos(2\lambda_1 t) + b_2 \sin(2\lambda_1 t)\] para obtener una funciones como las que siguen:

arm_2 <- arm_1 |> 
  mutate(f_2 = f_1 + -3 * cos(2 * t * pi / 6) + 2 * sin(2 * t * pi / 6))
ggplot(arm_2, aes(x = t, y = f_2, colour = factor(n))) + geom_line() + 
  geom_point() +
  geom_vline(xintercept = c(1, 13, 25))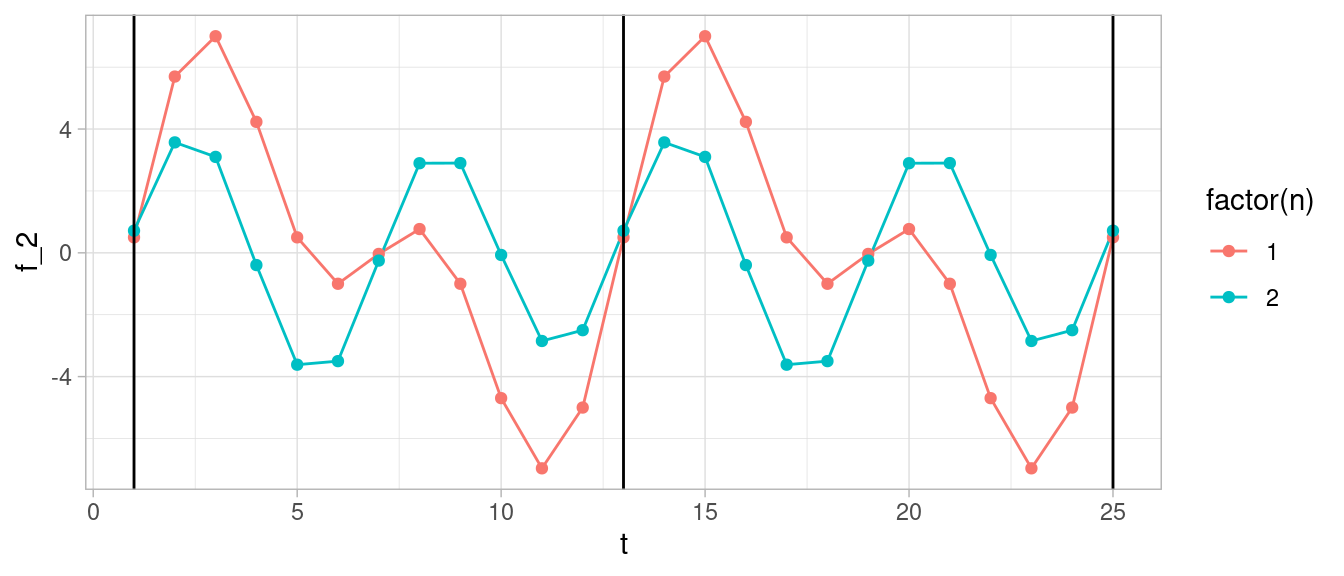

Y así sucesivamente. Cualquier función periodica puede aproximarse bien mediante una suma de cosenos y senos, siempre y cuando utilicemos suficientes armónicos.

Nota que en los ejemplos de arriba necesitamos dos coeficientes para cada armónico. La componente estacional del modelo podemos escribirla como (para estacionalidad constante):

\[\gamma_t = \sum_{j=1}^L (a_j \cos(\lambda_j t) + a^*_j \sin(\lambda_jt)).\] Y hacemos estocásticas estas componentes sustituyendo \[a_{j,t+1} = a_{j,t} + \omega_{j,t}, a^*_{j,t+1} = a^*_{j,t} + \omega^*_{j,t}\] donde las \(\omega,\omega^*\) son normales independientes con varianza \(\sigma_\omega^2\).

Esta es la forma más simple de agregar estacionalidad trigonométrica, pero tiene la desventaja de que los errores que agregamos se multiplican después por senos y cosenos, lo cual quiere decir que su efecto no es igual en diferentes partes del periodo. La otra forma más usual puedes verla en la ayuda de AddTrig de bsts o en la sección 3.2.1 de Durbin y Koopman (2001).

Nuestra primera parte del modelo es entonces (donde podemos ajustar el número de frecuencias o armónicos que incluímos comparando los modelos producidos):

modelo_natalidad_1 <- AddLocalLevel(list(), y = y) |> 
  AddSeasonal(nseasons = 7, y = y) |> 
  AddTrig(period = 365.25, frequencies = 1:3, y = y)

12.2.1 Días de asueto

Definiremos componentes para algunos de los días de asueto/especiales más importantes, considerando que su efecto puede ir más allá del día particular. En la versión estática, tenemos un coeficiente distinto para cada uno de esos días en la ventana que hayamos elegido:

año_nuevo <- NamedHoliday(holiday.name = "NewYearsDay", days.before = 4,
                          days.after = 4)
navidad <- NamedHoliday(holiday.name = "Christmas", days.before = 4,
                        days.after = 4)
pascua <- NamedHoliday(holiday.name = "EasterSunday", 
                       days.after = 5, days.before = 5)
feb_14 <- NamedHoliday(holiday.name = "ValentinesDay", 
                       days.after = 3, days.before = 3)
halloween <- NamedHoliday(holiday.name = "Halloween", 
                       days.after = 5, days.before = 5)
sept_16 <- FixedDateHoliday(holiday.name = "Independencia", 
                        month = "September", day = 16, days.before = 2,
                        days.after = 2)
mayo_1 <- FixedDateHoliday(holiday.name = "Trabajo",
                       month = "May", day = 1, days.before = 2,
                       days.after = 2)

Y nuestro modelo es entonces, agregando también un coeficiente para febrero 29 y marzo 1 cuando sigue de 29 de febrero:

modelo_natalidad <- AddLocalLevel(list(), y = y) |> 
  AddSeasonal(nseasons = 7, y = y) |> 
  AddTrig(period = 365.25, frequencies = 1:3, y = y) |> 
  AddRandomWalkHoliday(holiday = año_nuevo, y = y) |> 
  AddRandomWalkHoliday(holiday = navidad, y = y,) |> 
  AddRandomWalkHoliday(holiday = pascua, y = y) |> 
  AddRandomWalkHoliday(holiday = feb_14, y = y) |> 
  AddRandomWalkHoliday(holiday = halloween, y = y) |> 
  AddRandomWalkHoliday(holiday = sept_16, y = y) |>
  AddRandomWalkHoliday(holiday = mayo_1, y = y) |> 
  AddDynamicRegression(y ~ feb_29 + mar_1_feb_29)
#ajuste_nat <- bsts(y, modelo_natalidad, niter = 1000)
ajuste_nat <- read_rds("cache/ajuste_nat.rds")
mean_contrib <- ajuste_nat$state.contributions |> 
  apply(c(2, 3), mean)
mean_contrib_tbl <- mean_contrib |> t() |> as_tibble() |> 
  mutate(fecha = natalidad_tbl$fecha) |> 
  mutate(trend_c = trend - mean(trend)) |> 
  select(-trend) |> 
  pivot_longer(cols = c(seasonal.7.1:dynamic, trend_c),
               names_to = "componente", values_to = "valor")
ggplot(mean_contrib_tbl, aes(x = fecha, y = valor)) +
  facet_wrap(~ componente) + geom_point()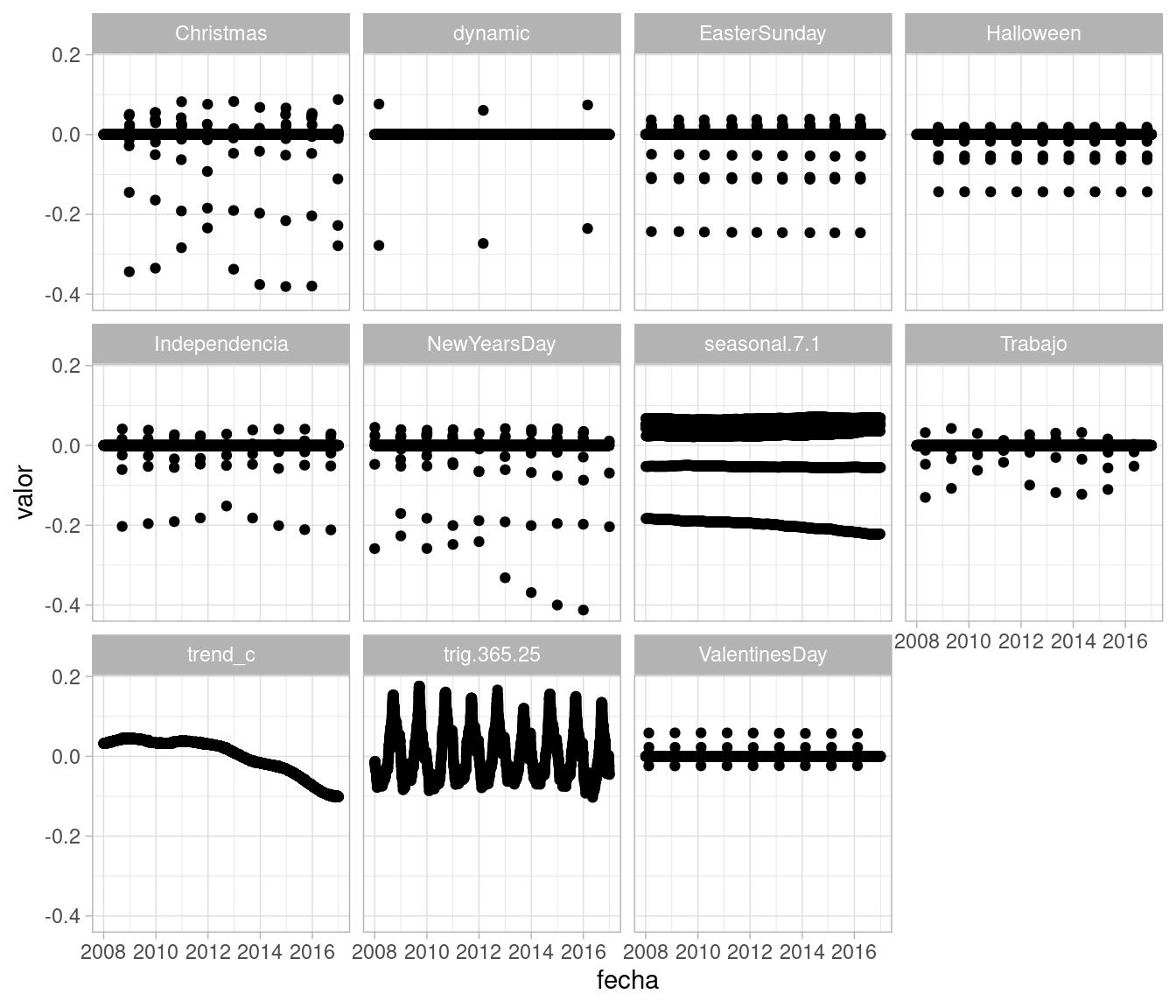

Podemos ver con más detalle cómo es el efecto de los días de asueto y sus “hombros”, tomando por ejemplo una parte 2008-2009 vemos la estructura:

ggplot(mean_contrib_tbl |> 
         filter(year(fecha) == 2009 & month(fecha) < 5 |
                year(fecha) == 2008 & month(fecha) >= 12), 
       aes(x = fecha, y = valor)) +
  facet_wrap(~ componente) + geom_line() + geom_point(size = 0.5)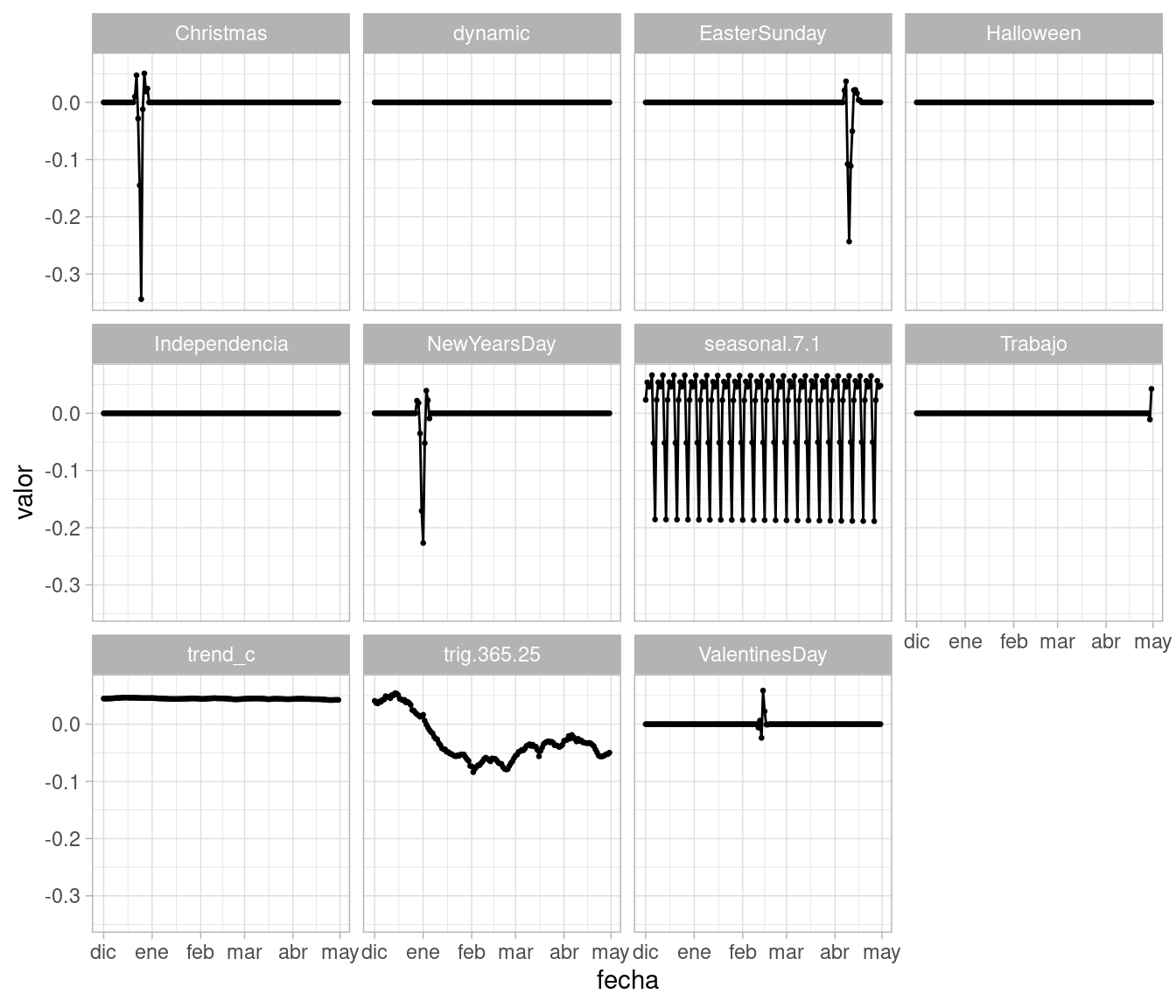

Nota: este modelo todavía requiere considerar qué otros efectos adicionales están actuando. La distribución de errores a un paso tiene colas largas, y todavía hay cierta información que podríamos usar para mejorar las predicción si consideramos la ACF de las innovaciones:

error <- ajuste_nat$one.step.prediction.errors |> apply(2, mean)
error_sin_2008 <- error[-c(1:365)]
qqnorm(error_sin_2008)
qqline(error_sin_2008)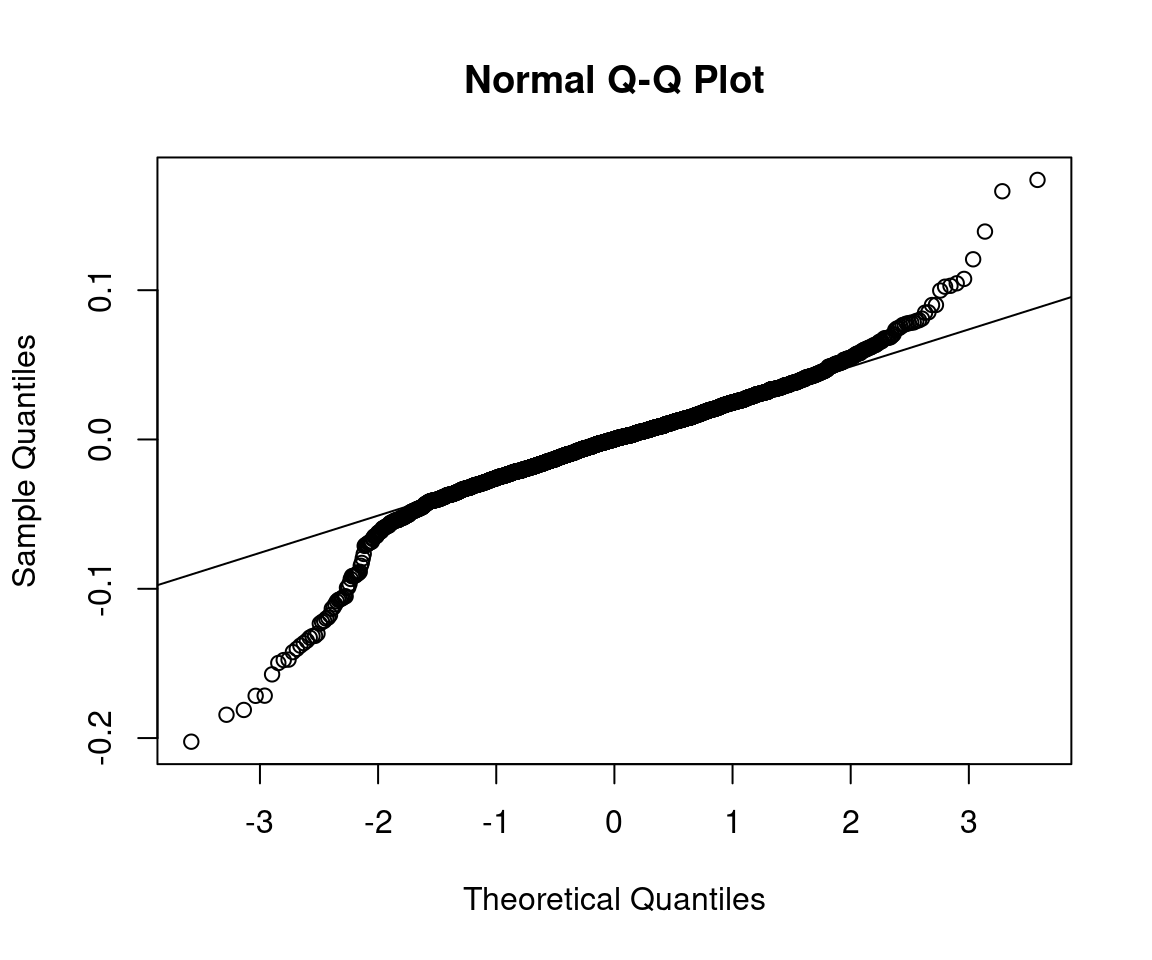

natalidad_tbl$error <- error
ACF(natalidad_tbl |> filter(year(fecha) > 2008), 
    error) |> autoplot() + ylim(c(-1,1))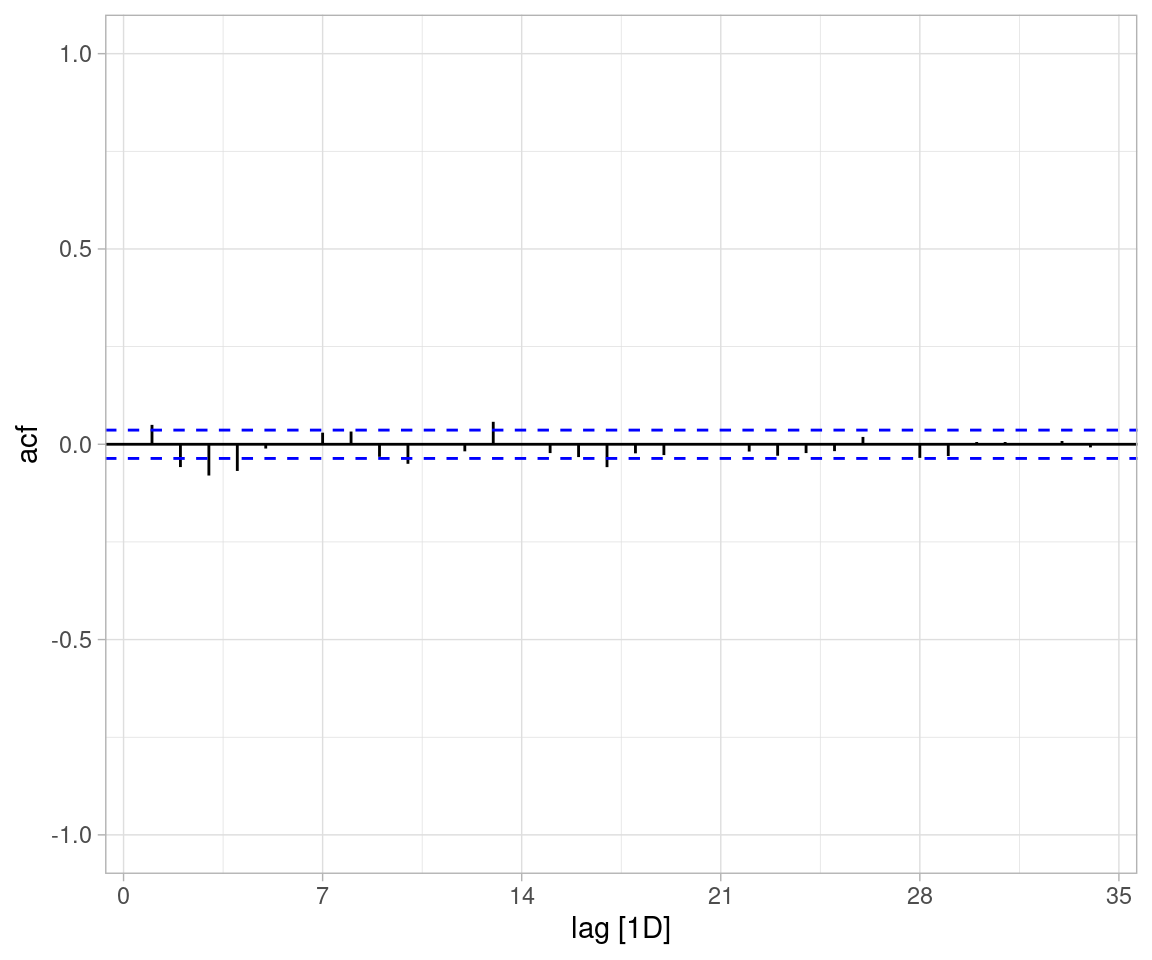

natalidad_tbl |> 
  filter(year(fecha) > 2008) |> 
  arrange(desc(abs(error))) |> 
  mutate(dia_sem = weekdays(fecha)) 
Warning: Current temporal ordering may yield unexpected results.
ℹ Suggest to sort by ``, `fecha` first.
Current temporal ordering may yield unexpected results.
ℹ Suggest to sort by ``, `fecha` first.
Current temporal ordering may yield unexpected results.
ℹ Suggest to sort by ``, `fecha` first.
# A tsibble: 2,922 x 5 [1D]
   fecha      nacimientos feb_29  error dia_sem
   <date>           <dbl>  <dbl>  <dbl> <chr>  
 1 2013-01-01        8.45      0 -0.202 martes 
 2 2009-11-02        8.64      0 -0.184 lunes  
 3 2012-12-25        8.47      0 -0.181 martes 
 4 2012-09-16        8.66      0  0.174 domingo
 5 2016-11-21        8.49      0 -0.172 lunes  
 6 2016-12-25        8.15      0  0.166 domingo
 7 2015-11-16        8.56      0 -0.157 lunes  
 8 2012-11-19        8.66      0 -0.150 lunes  
 9 2014-03-17        8.55      0 -0.148 lunes  
10 2011-11-21        8.69      0 -0.147 lunes  
# ℹ 2,912 more rows
  • En la tabla de arriba vemos que falta incluir algunos otros días de asueto, los que feriados que se mueven a los lunes.
  • También días feriados con fecha fija que caen en Domingo tienen un efecto distinto (es posible construir manualmente la serie de días de asueto excluyendo los feriados que caen en domingo, por ejemplo).

12.3 Nowcasting y uso de covariables

Nowcasting

En nowcasting buscamos predecir los valores contemporáneos de una serie de tiempo que, por retrasos en reporte, no tenemos disponibles. Usualmente utilizamos variables asociadas contemporáneas que sí están disponibles, y se trata de pronósticos a corto plazo

Un ejemplo es el indicador oportuno de actividad económica que se publica mensualmente. Este indicador busca estimar el IGAE (indicador global de actividad económica), y utiliza variables económicas, financieras y otras, disponibles al momento (mientras que el IGAE se publica con unos dos meses de retraso). Ver aquí: https://www.inegi.org.mx/investigacion/ioae/.

Una estrategia puede ser incluír variables relevantes cómo en regresión dinámica. Sin embargo, si estamos buscando entre una cantidad relativamente grande de predictores, es posible obtener mejores resultados haciendo selección de variables. En el caso de bsts se utiliza una inicial de spike-slab, que es una mezcla de una masa de probabilidad mayor a 0 para un valor del coeficiente igual a 0 (es decir, la variable está excluída del modelo), y una distribución normal centrada en 0 (el coeficiente puede tomar un valor positivo o negativo).

En este ejemplo consideraremos (Scott y Varian (2015)) el pronóstico oportuno de los números semanales reclamaciones pagos de seguro de desempleo en Estados Unidos, que se reportan varios días después de que cierra cada semana. En el artículo citado, utilizan medidas relativa de popularidad de búsquedas relacionadas con desempleo en Google, que se pueden tener de manera completa en cuanto la semana cierra. Ver también aquí o aquí.

Este código está adaptado de aqui, ver también este reporte.

Primero construiremos un modelo con tendencia lineal y estacionalidad. En este caso, como consideramos una serie relativamente corta (no más de 10 años), y la estacionalidad es dinámica, podemos usar un periodo de 52 semanas, aún cuando sabemos que algunos años tienen 53 semanas.

data(iclaims)     
original.claims <- initial.claims
initial.claims <- original.claims[1:436, ]
new.data <- original.claims[437:456, ]
ss <- AddLocalLinearTrend(list(), initial.claims$iclaimsNSA)
ss <- AddSeasonal(ss, initial.claims$iclaimsNSA, nseasons = 52)
model1 <- bsts(initial.claims$iclaimsNSA,
               state.specification = ss,
               niter = 1000)
=-=-=-=-= Iteration 0 Wed May 15 13:43:34 2024 =-=-=-=-=
=-=-=-=-= Iteration 100 Wed May 15 13:43:38 2024 =-=-=-=-=
=-=-=-=-= Iteration 200 Wed May 15 13:43:41 2024 =-=-=-=-=
=-=-=-=-= Iteration 300 Wed May 15 13:43:45 2024 =-=-=-=-=
=-=-=-=-= Iteration 400 Wed May 15 13:43:48 2024 =-=-=-=-=
=-=-=-=-= Iteration 500 Wed May 15 13:43:52 2024 =-=-=-=-=
=-=-=-=-= Iteration 600 Wed May 15 13:43:55 2024 =-=-=-=-=
=-=-=-=-= Iteration 700 Wed May 15 13:43:58 2024 =-=-=-=-=
=-=-=-=-= Iteration 800 Wed May 15 13:44:02 2024 =-=-=-=-=
=-=-=-=-= Iteration 900 Wed May 15 13:44:05 2024 =-=-=-=-=
plot(model1)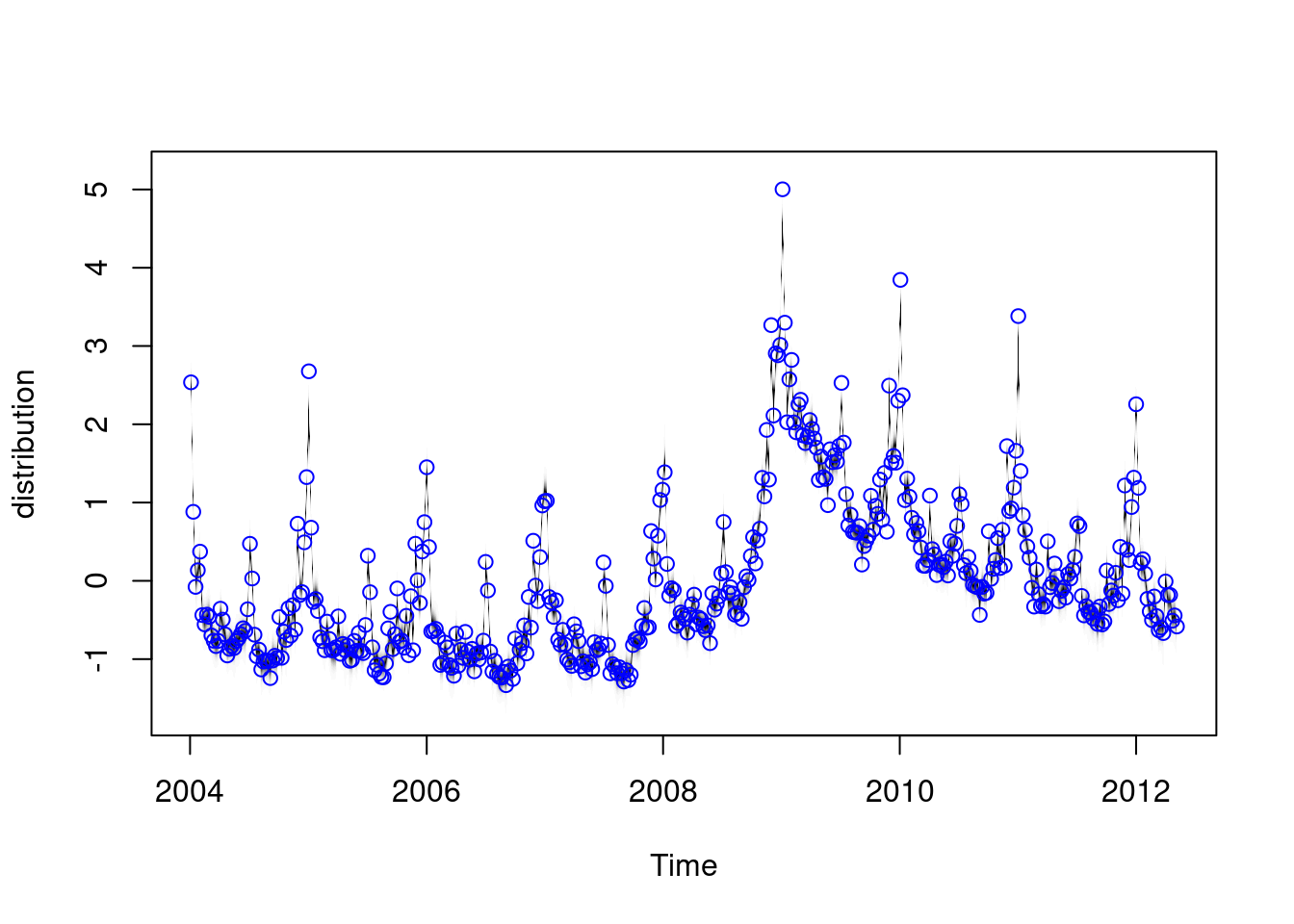

plot(model1, "components")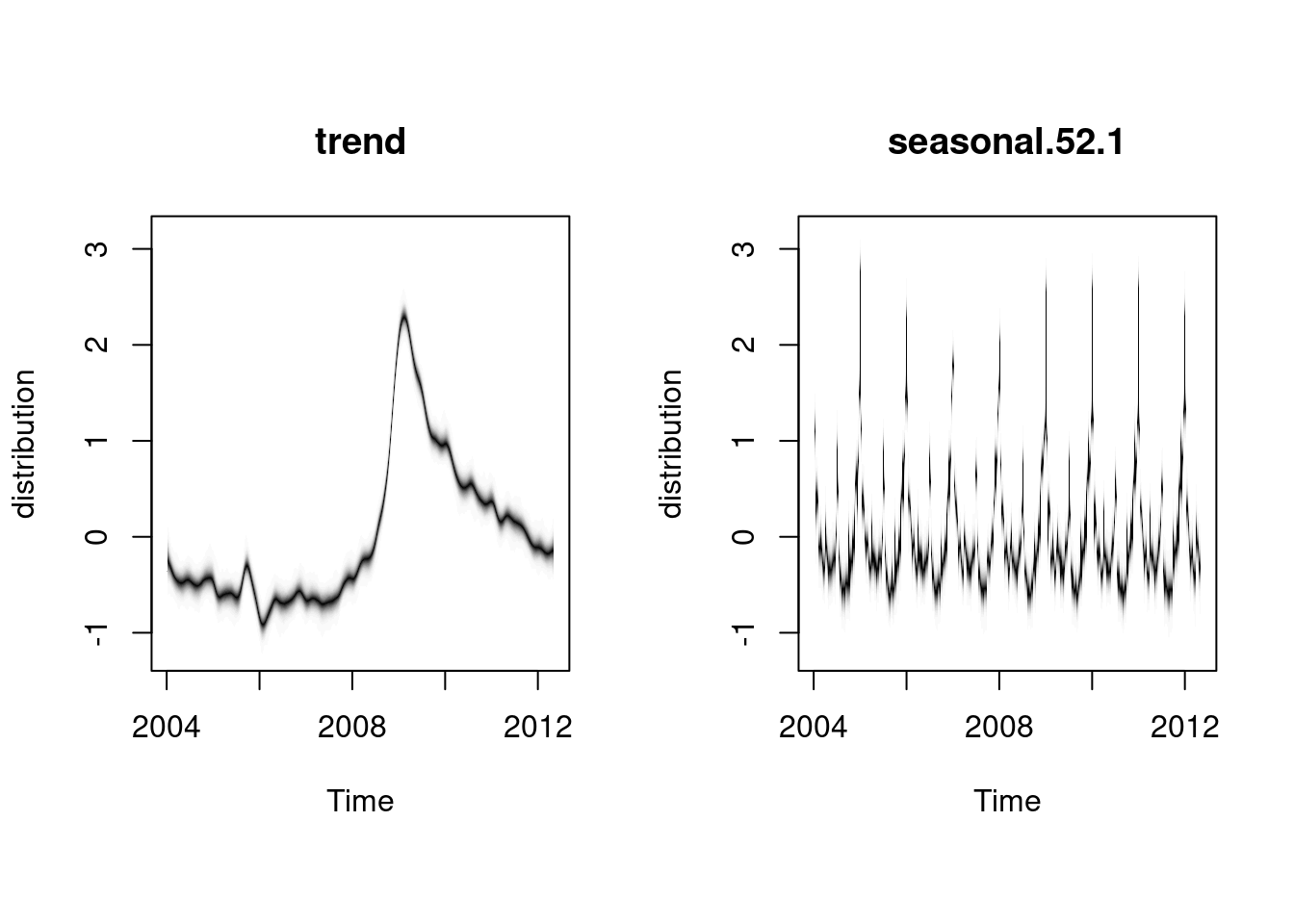

Y podemos construir predicciones:

pred1 <- predict(model1, horizon = 12)
plot(pred1, plot.original = 156)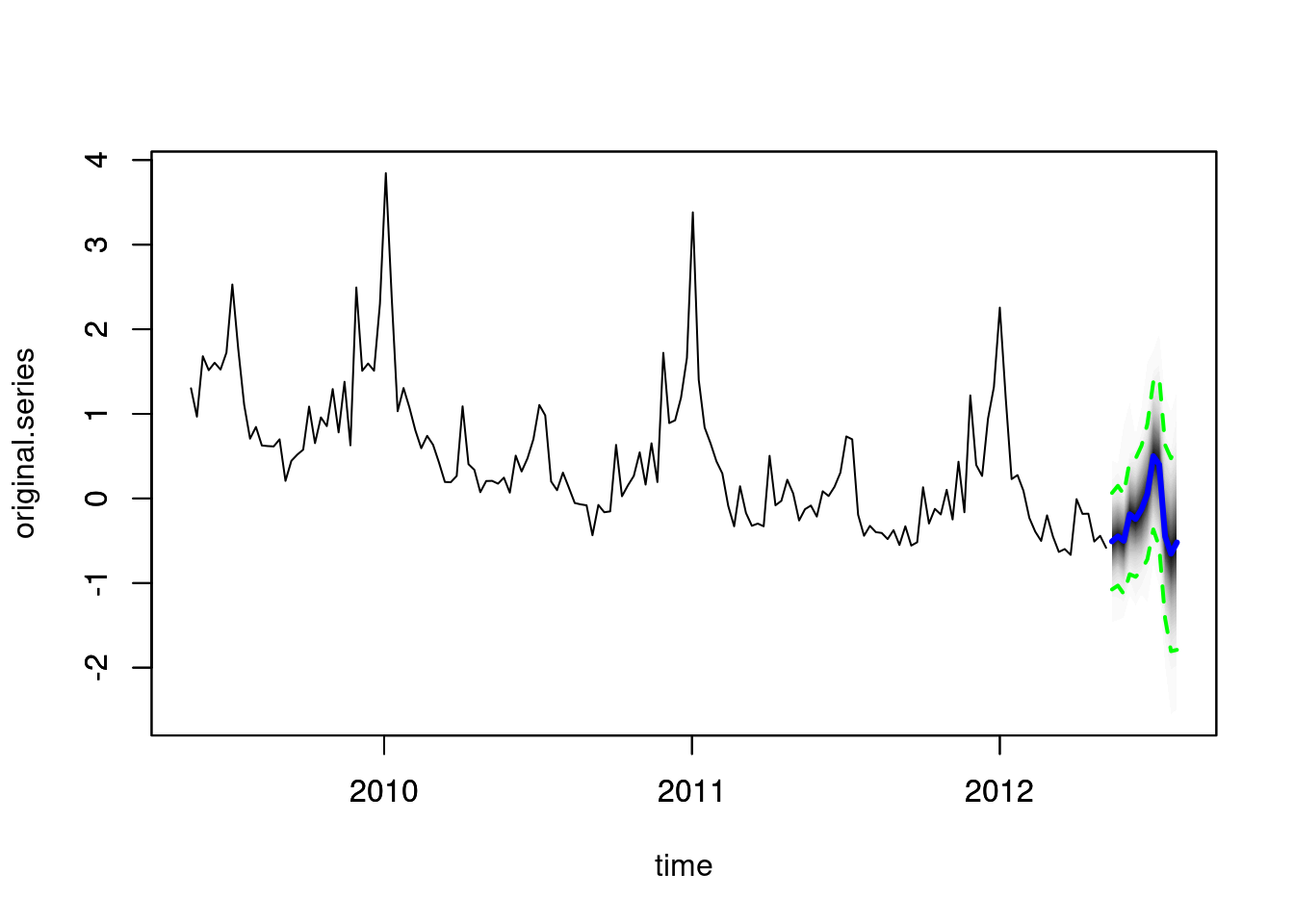

Entre las variables de términos de búsqueda están

names(initial.claims)[-1]
 [1] "michigan.unemployment"      "idaho.unemployment"        
 [3] "pennsylvania.unemployment"  "unemployment.filing"       
 [5] "new.jersey.unemployment"    "department.of.unemployment"
 [7] "illinois.unemployment"      "rhode.island.unemployment" 
 [9] "unemployment.office"        "filing.unemployment"

Seleccionamos una inicial para el tamaño esperado del modelo (y después seleccionamos según desempeño predictivo):

model2 <- bsts(iclaimsNSA ~ .,
               state.specification = ss,
               niter = 1000,
               data = initial.claims, 
               expected.model.size = 2)
=-=-=-=-= Iteration 0 Wed May 15 13:44:10 2024 =-=-=-=-=
=-=-=-=-= Iteration 100 Wed May 15 13:44:13 2024 =-=-=-=-=
=-=-=-=-= Iteration 200 Wed May 15 13:44:17 2024 =-=-=-=-=
=-=-=-=-= Iteration 300 Wed May 15 13:44:20 2024 =-=-=-=-=
=-=-=-=-= Iteration 400 Wed May 15 13:44:23 2024 =-=-=-=-=
=-=-=-=-= Iteration 500 Wed May 15 13:44:27 2024 =-=-=-=-=
=-=-=-=-= Iteration 600 Wed May 15 13:44:30 2024 =-=-=-=-=
=-=-=-=-= Iteration 700 Wed May 15 13:44:34 2024 =-=-=-=-=
=-=-=-=-= Iteration 800 Wed May 15 13:44:37 2024 =-=-=-=-=
=-=-=-=-= Iteration 900 Wed May 15 13:44:41 2024 =-=-=-=-=
model3 <- bsts(iclaimsNSA ~ .,
               state.specification = ss,
               niter = 1000,
               data = initial.claims,
               expected.model.size = 6)  # Passed to SpikeSlabPrior.
=-=-=-=-= Iteration 0 Wed May 15 13:44:44 2024 =-=-=-=-=
=-=-=-=-= Iteration 100 Wed May 15 13:44:48 2024 =-=-=-=-=
=-=-=-=-= Iteration 200 Wed May 15 13:44:51 2024 =-=-=-=-=
=-=-=-=-= Iteration 300 Wed May 15 13:44:55 2024 =-=-=-=-=
=-=-=-=-= Iteration 400 Wed May 15 13:44:58 2024 =-=-=-=-=
=-=-=-=-= Iteration 500 Wed May 15 13:45:02 2024 =-=-=-=-=
=-=-=-=-= Iteration 600 Wed May 15 13:45:05 2024 =-=-=-=-=
=-=-=-=-= Iteration 700 Wed May 15 13:45:09 2024 =-=-=-=-=
=-=-=-=-= Iteration 800 Wed May 15 13:45:12 2024 =-=-=-=-=
=-=-=-=-= Iteration 900 Wed May 15 13:45:16 2024 =-=-=-=-=

Comparamos los modelos con el error de pronóstico a un paso, y el modelo 2 es el de mejor desempeño:

CompareBstsModels(list("Modelo s.vars" = model1,
                       "Modelo esp2" = model2,
                       "Modelo esp6" = model3),
                  colors = c("black", "red", "blue"))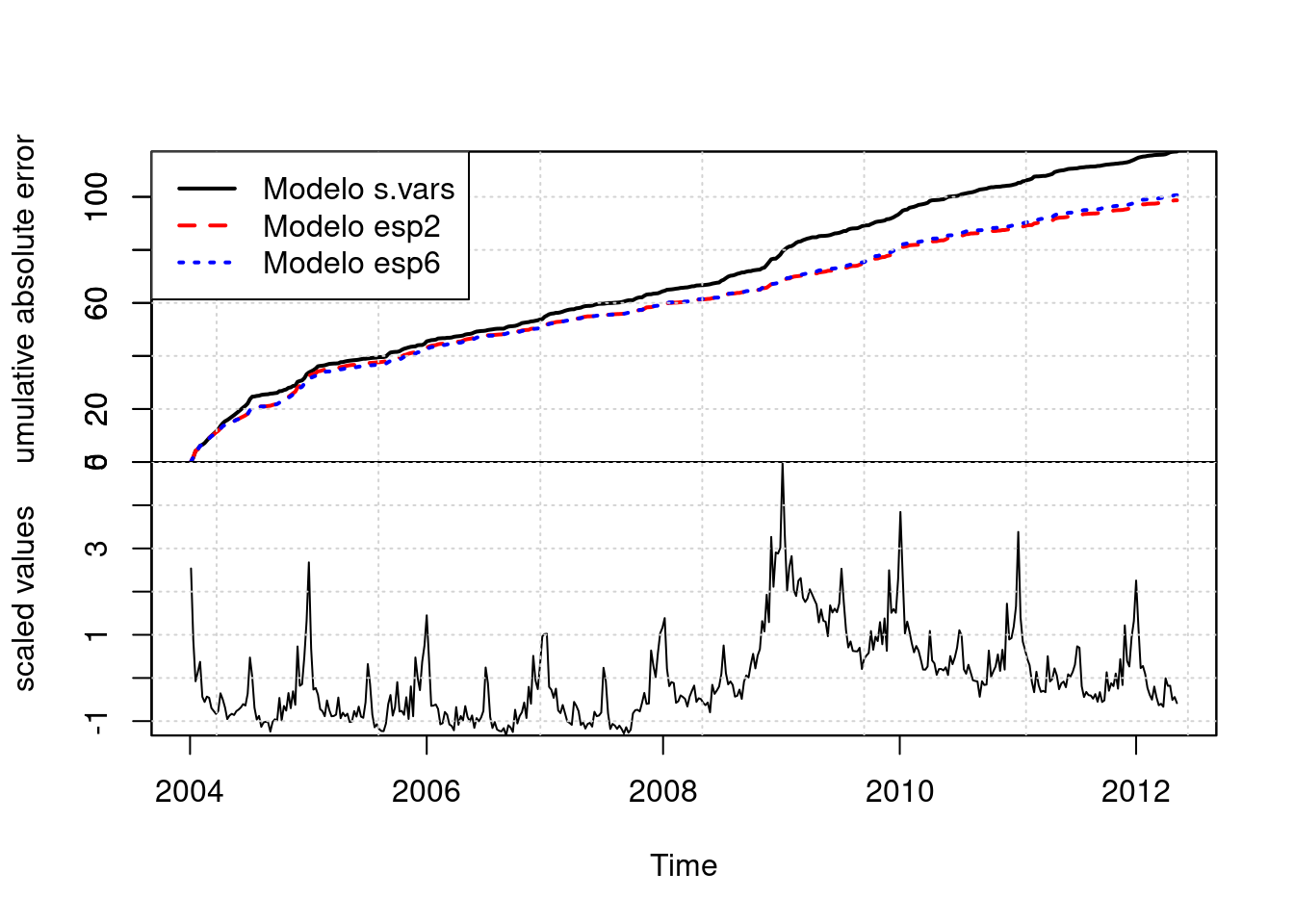

pred2 <- predict(model2, horizon = 12, newdata = new.data[1:12, ])
plot(pred2, plot.original = 156)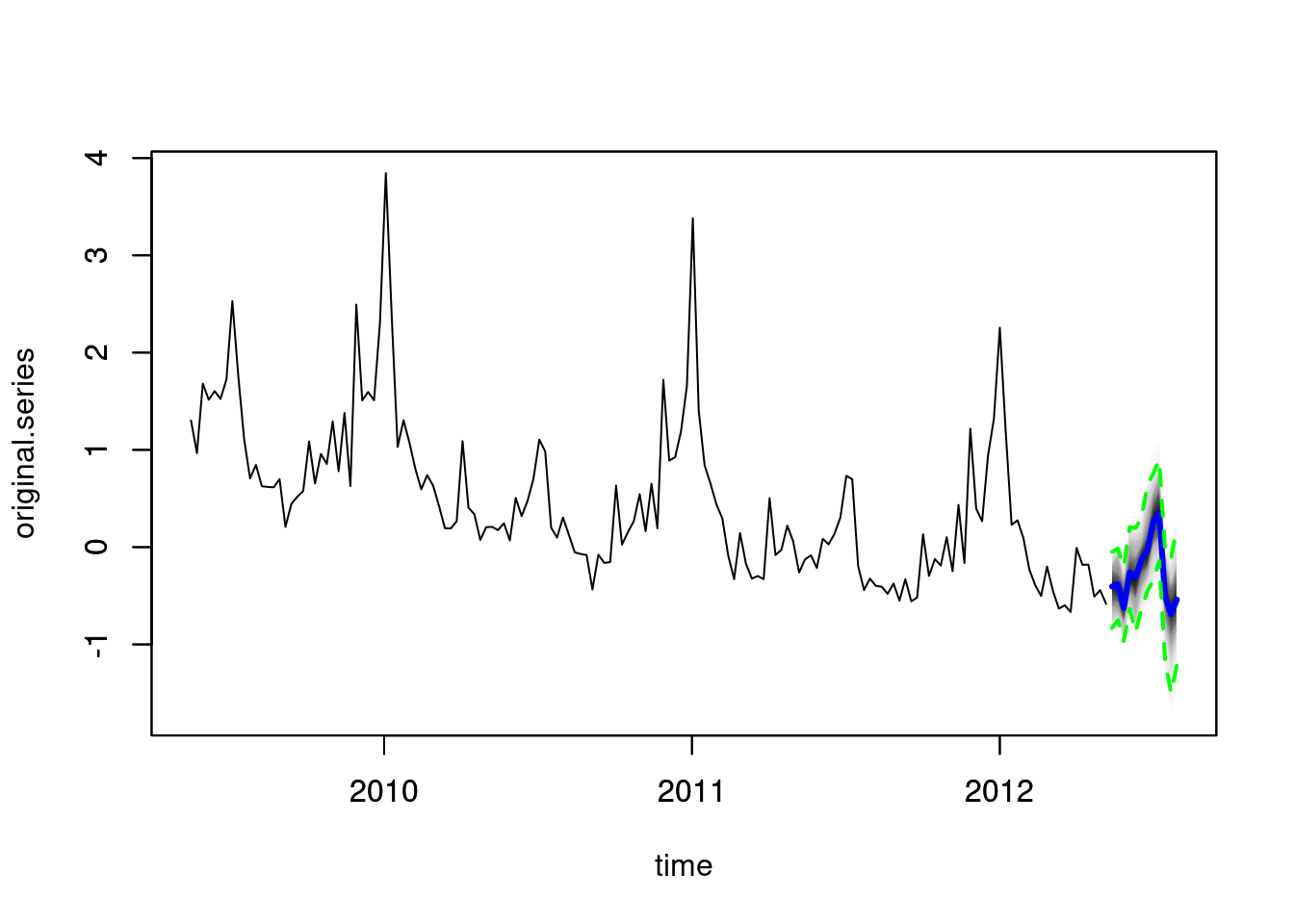

Podemos ver qué variables fueron seleccionadas:

plot(model2, "coefficients")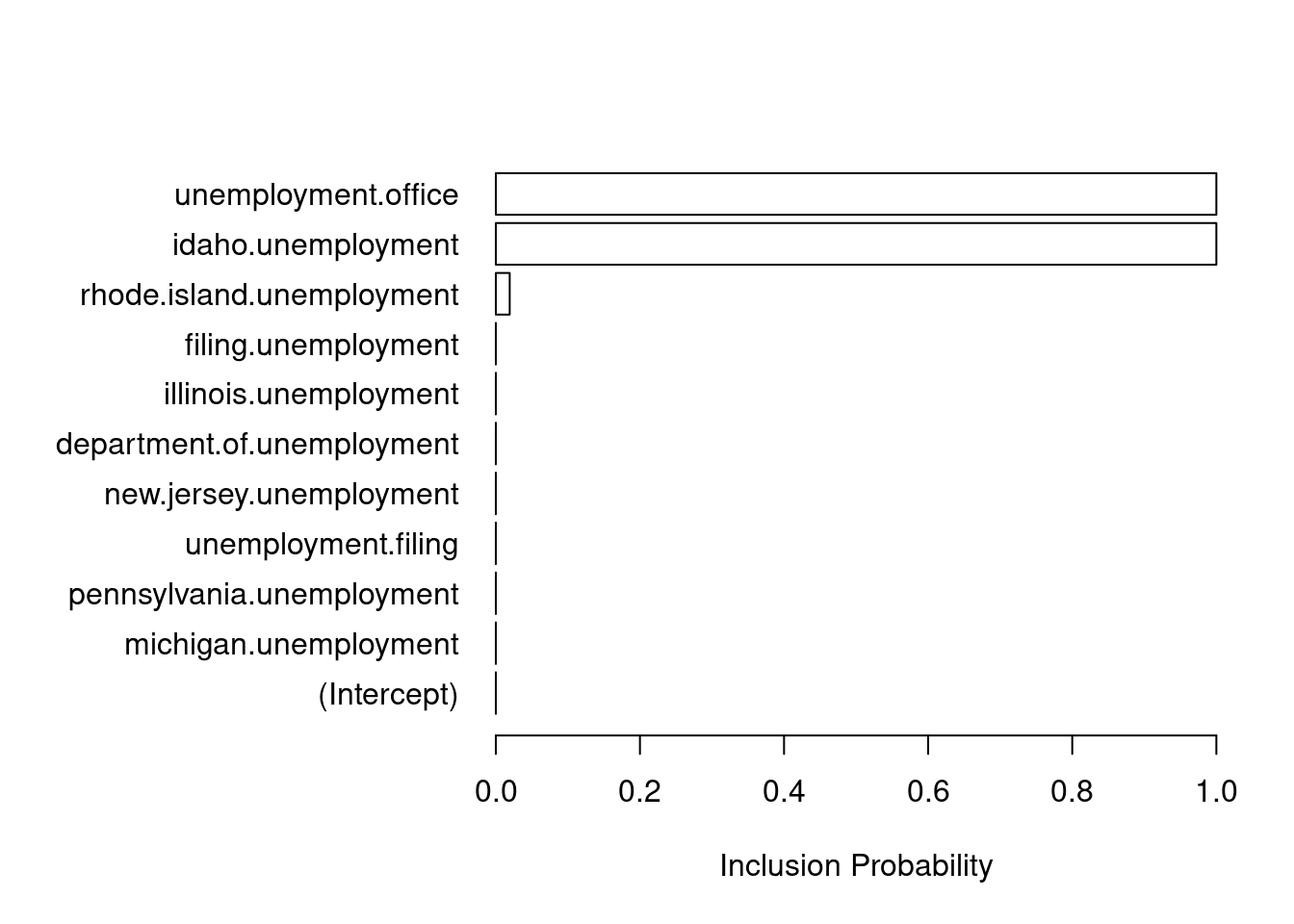

12.4 Agregación de encuestas

Para cada elección, se publica en México un gran número de encuestas sobre las preferencias partidistas. Con el fin de obtener una estimación de las preferencias subyacentes, las encuestas pueden combinarse en una encuesta de encuestas. Mostramos un modelo dinámico bayesiano para combinar encuestas y producir una única estimación.

library(lubridate)
mex_2018_tbl <- 
  read_csv("../datos/wiki_encuestas_2018_en_campana.csv") |> 
  mutate(id_encuesta = row_number()) |> 
  select(id_encuesta, everything()) |> 
  mutate(Muestra = as.numeric(Muestra)) |> 
  mutate(margen_error = str_remove(`Margen de error`, "±" )) |> 
  mutate(margen_error = as.numeric(margen_error)) |> 
  rowwise() |> 
  mutate(no_contesto = 
    sum(`Ninguno Nulo/Blanco`, `NC/NS`, na.rm = TRUE)) |> 
  ungroup() |> 
  select(-c(`Margen de error`, `Ninguno Nulo/Blanco`, `NC/NS`)) |> 
  mutate(Zavala = ifelse(is.na(Zavala), 0, Zavala)) |> 
  mutate(Rodríguez = ifelse(is.na(Rodríguez ), 0, Rodríguez )) |> 
  mutate(Otros = Zavala + Rodríguez) |> 
  mutate(publicacion = dmy(paste(`Publicación (2018)`, 2018))) |> 
  select(id_encuesta, Encuestadora, publicacion, Muestra, 
         Obrador:Meade, Otros, no_contesto, margen_error)

Generalmente las casas encuestadores usan una fórmula simple para el error, como si fuera muestreo aleatorio simple, que rara vez se usa en la práctica (para encuestas casa por casa, por ejemplo), y no toma el cuenta de que muchas veces se usan reponderaciones de los datos. Ambas cosas generalmente producen varianzas considerablemente más altas.

ggplot(mex_2018_tbl, aes(
    x = margen_error, y = round(100 / sqrt(Muestra),1))) +
  geom_point() + geom_abline()
Warning: Removed 11 rows containing missing values or values outside the scale range
(`geom_point()`).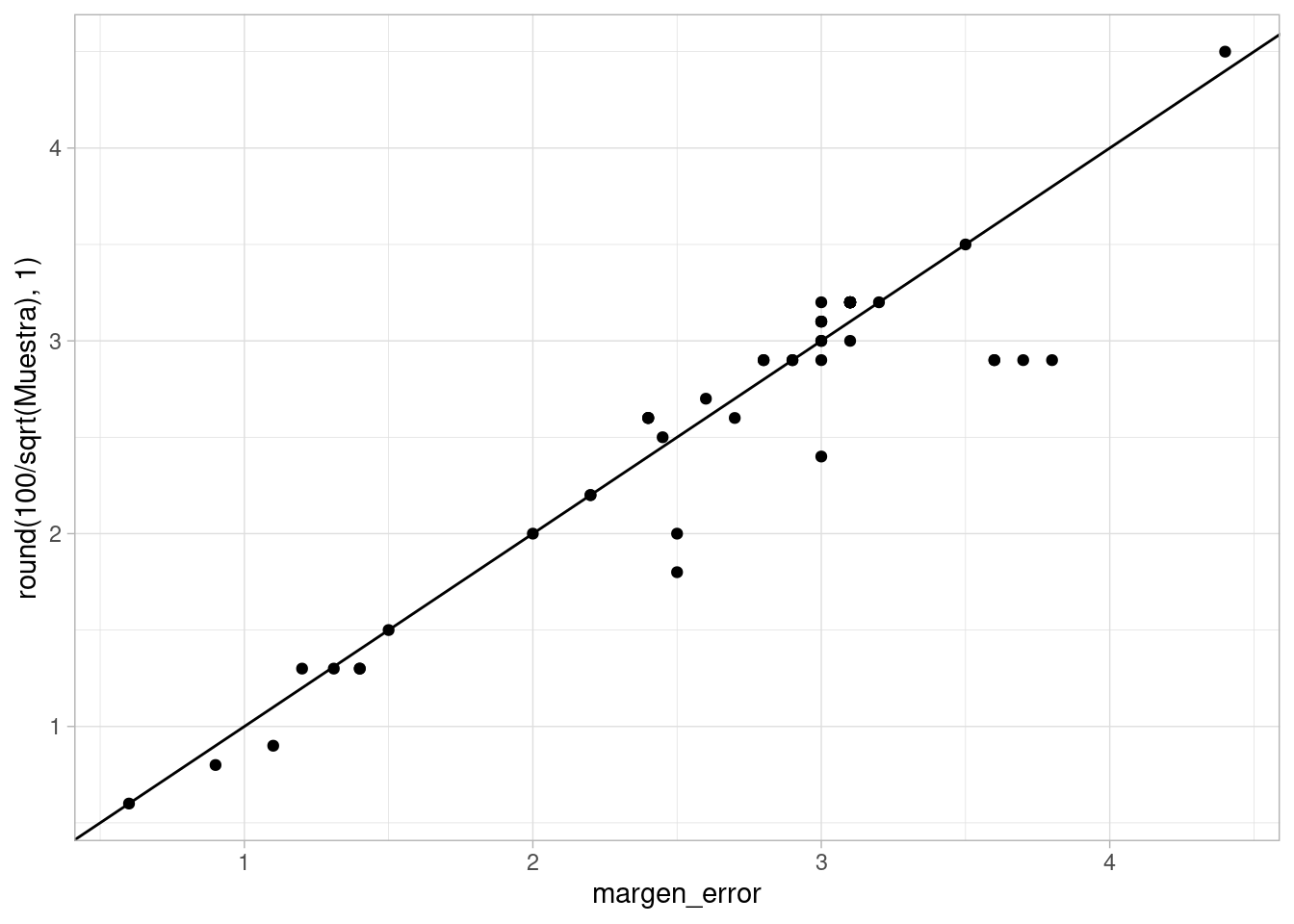

Supondremos margen de error de 6 para aquellos que no reportan tamaño de muestra o error, y usamos un factor de diseño igual a 2. Adicionalmente, como buscamos preferencias efectivas, descontamos aquellos que no reportaron preferencia:

# suponemos margen de error 6 para las que no reportan
# generalmente se reporta el error para un porcentaje de 50%
# como si fuera muestreo aleatorio simple
# Usamos un factor de diseño igual a 2
mex_2018_tbl <- mex_2018_tbl |> 
  mutate(margen_error = ifelse(is.na(margen_error), 6, margen_error)) |> 
  mutate(n_inf = (100 / (sqrt(2) * margen_error))^2) |> 
  mutate(n_efectiva = n_inf * (Obrador + Anaya + Meade + Otros)/100)

Finalmente, normalizamos a preferencia efectiva:

pref_tbl <- mex_2018_tbl |> 
  pivot_longer(Obrador:Otros, names_to = "candidato", 
               values_to = "pref_cruda") |> 
  group_by(id_encuesta) |> 
  mutate(p = pref_cruda / sum(pref_cruda)) |> 
  mutate(n_cand = p * n_efectiva) |> 
  select(-c(p, pref_cruda)) |> 
  pivot_wider(names_from = candidato, values_from = n_cand)

Ahora consideramos el modelo de observaciones que utilizaremos. En primer lugar, las observaciones son conteos, que suponemos multinomiales:

\[n_i \sim \textrm{Multinom}(\pi_i, N_{i}^{eff})\] donde \(n_i\) es el vector de conteos observado, \(N_i^{eff}\) es la muestra efectiva, y \(\pi_i\) es el vector de preferencias de los candidatos para la encuesta \(i\). Ahora definimos \(\mu_i\) tal que \[\textrm{softmax}(\mu_i) = \pi_i\] Ahora consideramos \(\mu_i\) para cada encuesta. Esta cantidad dependerá de:

  • La preferencia subyacente \(p(t_i)\) de los votantes al tiempo \(t_i\) que se tomó la encuesta \(i\).
  • Sesgos propios de la casa encuestadora \(c(i)\), que hizo la encuesta \(i\), que denotamos como \(d_{c(i)}\). Estos ocurren porque diversas metodologías alcanzan a distintos sectores de posibles votantes, o consideran diferentes poblaciones objetivo. Suponemos que en promedio sobre las casas encuestadores, este valor es cercano a cero.
  • Sesgos general \(b\) en el que incurren todas las casas encuestadoras. Este error sistemático ocurre por ejemplo, cuando un sector particular no responde a encuestas, y también tiene preferencias distintas a las de la población general.

El modelo entonces es

\[\mu_i = \alpha(t_i) + b + d_{c(i)}\] Nuestro interés es estimar \(\alpha(t)\) para cada \(t\), y en consecuencia nuestra estimación de la preferencia será

\[p (t) = \textrm{softmax}(\alpha(t)),\] es decir, la preferencia quitando el sesgo de casa encuestadora y el sesgo general de todas las encuestas. Buscaremos hacer una proyección \(p(T)\) si \(T\) es el día de la elección.

Ahora construímos la parte dinámica del modelo. Supondremos los sesgos generales y por casas encuestadoras como fijos en el tiempo (esto puede cambiarse si existen cambios de metodología en el tiempo por ejemplo).

En este ejemplo usaremos el modelo más simple de nivel local, como en en este modelo de elecciones en Alemania, o el modelo del Economist para la elección presidencial de 2020:

  • Modelo de nivel local, donde los choques ocurren cada día y cambian las preferencias. Las predicciones al día de la elección son las últimas estimaciones junto con la incertidumbre asociada a la evolución de las preferencias.
  • Otra alternativa es también modelar tendencia (usual o autorregresiva), si consideramos que el “momento” de los candidatos es importante. Las predicciones al día de elección incluyen esa tendencia.

En este caso, tenemos usaremos (recuerda que la longitud de \(p\) es el número de candidatos). En primer lugar, ponemos

\[\alpha(t+1) = \alpha(t) + \epsilon(t)\] con \(\epsilon(t) \sim NMV(0, W)\), donde \(W\) es una matriz de varianzas y covarianzas para los choques, que pueden tener patrones de correlación entre candidatos.

primer_dia <- pref_tbl$publicacion |> min()
ultimo_dia <- pref_tbl$publicacion |> max()
fecha_eleccion <- lubridate::ymd("2018-07-01")
#dias_tbl <- tibble(dia = seq(primer_dia, fecha_eleccion, by = "day")) |> 
#  mutate(id_dia = row_number())
dias_tbl <- read_csv("../datos/dias.csv")
Rows: 92 Columns: 2
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl  (1): id_dia
date (1): dia

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
# identificar dias
pref_tbl <- pref_tbl |> 
  left_join(dias_tbl |> rename(publicacion = dia)) |> 
  ungroup()
Joining with `by = join_by(publicacion)`
# numerar casas
pref_tbl <- pref_tbl |> ungroup() |> 
  mutate(id_casa = as.integer(factor(Encuestadora)))
cands_tbl <- pref_tbl |> pivot_longer(Obrador:Otros, names_to = "candidato",
                                      values_to = "n_pref") |> 
  group_by(id_encuesta) |> 
  mutate(porcentaje_pref = 100 * n_pref / sum(n_pref))

Y podemos usar un modelo como el que sigue:

library(cmdstanr)
mod_elecciones <- cmdstan_model("./src/series-de-tiempo/modelo-eleccion.stan")
print(mod_elecciones)
data {
  int<lower=0> N; //num encuestas
  int<lower=0> T; //num dias
  int<lower=0> K; //num candidatos
  int<lower=0> S; //num casas
  array[N, K] int n_obs;   //preferencias
  array[N] int num_casa_enc;
  array[N] int dia_enc;
}

parameters {

  cholesky_factor_corr[K] L_Omega;
  vector<lower=0>[K] sigma;
  array[T] vector[K] eta;
  vector[K] alpha_1;
  array[S] vector[K] d_casa;
  vector[K] b;

}

transformed parameters {
  array[N] simplex[K] mu;
  array[T] vector[K] alpha;
  array[S] vector[K] d_casa_c;

  alpha[1] = alpha_1;
  // nivel local
  for(t in 2:T){
    alpha[t] = alpha[t-1] +  diag_pre_multiply(sigma, L_Omega) *  eta[t];
  }
  // modelo para la media
  for(s in 1:S){
    d_casa_c[s] = d_casa[s] - mean(d_casa[s]);
  }
  for(i in 1:N){
    mu[i] = softmax(alpha[dia_enc[i]] + d_casa_c[num_casa_enc[i]] + b);
  }
}

model {
  for(i in 1:N){
    n_obs[i] ~ multinomial(mu[i]);
  }

  alpha_1 ~ normal(0, 2);
  for(t in 1:T) {
    eta[t] ~ std_normal();
  }
  b ~ normal(0, 0.07);
  for(s in 1:S){
    d_casa[s] ~ normal(0, 0.25);
  }
  L_Omega ~ lkj_corr_cholesky(2);
  sigma ~ normal(0, 0.05);
}

generated quantities{
  corr_matrix[K] Omega;

  Omega = multiply_lower_tri_self_transpose(L_Omega);

}
n_obs <- pref_tbl |> 
  ungroup() |> 
  select(Obrador:Otros) |> 
  as.matrix() |> 
  apply(c(1,2), as.integer)

casas <- pref_tbl$id_casa
dia_enc <- pref_tbl$id_dia
datos_lst <- list(K = ncol(n_obs), N = nrow(n_obs), n_obs = n_obs + 1,
                  S = max(casas), num_casa_enc = casas,
                  dia_enc = dia_enc, T = max(dias_tbl$id_dia))
ajuste <- mod_elecciones$sample(data = datos_lst, 
  parallel_chains = 4, max_treedepth = 12, init = 0.01,
  step_size = 0.01, refresh = 1000,
  iter_sampling = 500, iter_warmup = 500)
Running MCMC with 4 parallel chains...

Chain 1 Iteration:   1 / 1000 [  0%]  (Warmup) 
Chain 2 Iteration:   1 / 1000 [  0%]  (Warmup) 
Chain 3 Iteration:   1 / 1000 [  0%]  (Warmup) 
Chain 4 Iteration:   1 / 1000 [  0%]  (Warmup) 
Chain 4 Iteration: 501 / 1000 [ 50%]  (Sampling) 
Chain 2 Iteration: 501 / 1000 [ 50%]  (Sampling) 
Chain 3 Iteration: 501 / 1000 [ 50%]  (Sampling) 
Chain 1 Iteration: 501 / 1000 [ 50%]  (Sampling) 
Chain 4 Iteration: 1000 / 1000 [100%]  (Sampling) 
Chain 4 finished in 196.1 seconds.
Chain 2 Iteration: 1000 / 1000 [100%]  (Sampling) 
Chain 2 finished in 205.3 seconds.
Chain 3 Iteration: 1000 / 1000 [100%]  (Sampling) 
Chain 3 finished in 208.4 seconds.
Chain 1 Iteration: 1000 / 1000 [100%]  (Sampling) 
Chain 1 finished in 210.2 seconds.

All 4 chains finished successfully.
Mean chain execution time: 205.0 seconds.
Total execution time: 210.3 seconds.

Extraemos la componente de interés, la resumimos y la transformamos a porcentaje de preferencia:

alpha_tbl <- ajuste$draws("alpha", format = "df") |> 
  pivot_longer(contains("alpha"), 
    names_to = "variable", values_to = "valor") |> 
  separate(variable, into = c("var", "id_dia", "cand"), 
           convert = TRUE, extra = "drop")
prop_tbl <- alpha_tbl |> group_by(.draw, id_dia) |> 
  mutate(valor = exp(valor)/sum(exp(valor))) |> 
  group_by(id_dia, cand) |> 
  summarise(media = mean(valor), q5 = quantile(valor, 0.05),
            q95 = quantile(valor, 0.95), .groups = "drop")

Y podemos var ahora las estimaciones suavizadas y los pronósticos desde el momento que terminaron las encuestas hasta el día de la elección:

cands_tbl <- cands_tbl |> 
  left_join(tibble(cand = 1:4, candidato = colnames(n_obs)))
prop_tbl <- prop_tbl |> 
  left_join(dias_tbl)
ggplot(prop_tbl, aes( y = 100 * media, group = factor(cand),
                     colour = factor(cand))) + 
  geom_line(aes(x = dia)) + 
  geom_ribbon(
    aes(x = dia,ymax = 100 * q95, ymin = 100 * q5, fill = factor(cand)), 
    alpha = 0.1, colour = NA) +
  geom_point(data = cands_tbl, aes(x = publicacion, y = porcentaje_pref), alpha = 0.4) + ylab("Preferencia")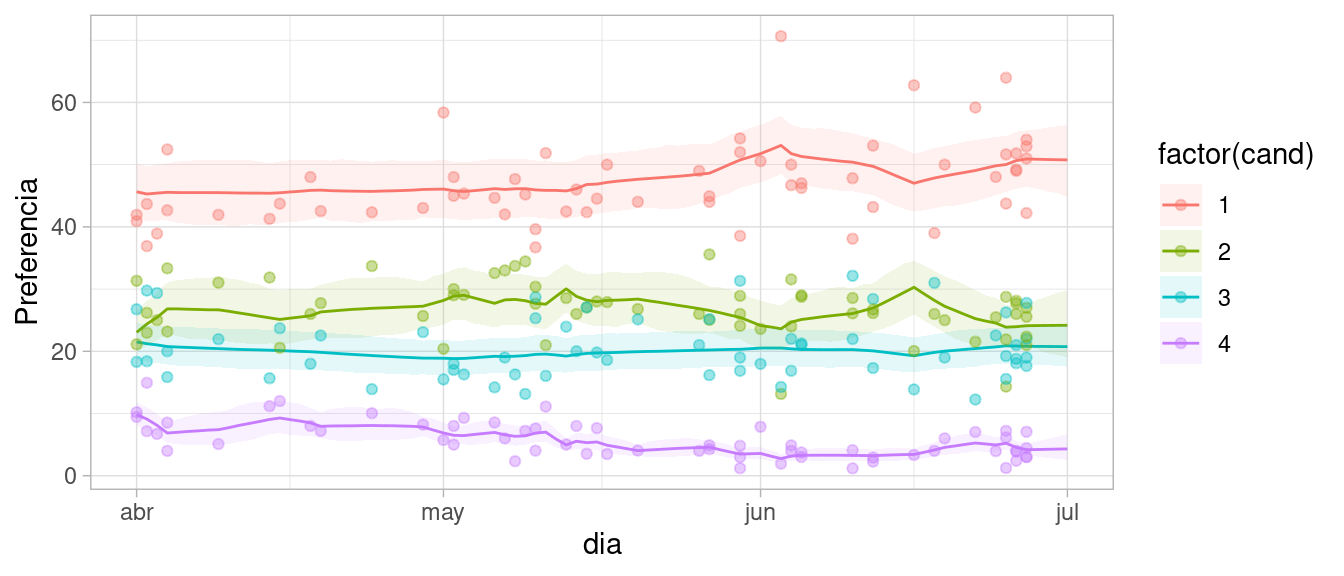

Por ejemplo la matriz de correlaciones estimada (para los choque del nivel) es:

ajuste$summary("Omega") |> select(variable, median, sd) |> 
  mutate(across(where(is.numeric), ~ round(.x, 3)))
# A tibble: 16 × 3
   variable   median    sd
   <chr>       <dbl> <dbl>
 1 Omega[1,1]  1     0    
 2 Omega[2,1]  0.033 0.352
 3 Omega[3,1]  0.125 0.404
 4 Omega[4,1] -0.231 0.339
 5 Omega[1,2]  0.033 0.352
 6 Omega[2,2]  1     0    
 7 Omega[3,2]  0.001 0.363
 8 Omega[4,2] -0.18  0.243
 9 Omega[1,3]  0.125 0.404
10 Omega[2,3]  0.001 0.363
11 Omega[3,3]  1     0    
12 Omega[4,3]  0.166 0.363
13 Omega[1,4] -0.231 0.339
14 Omega[2,4] -0.18  0.243
15 Omega[3,4]  0.166 0.363
16 Omega[4,4]  1     0

Este modelo tiene varias ventajas sobre hacer promedios simples o suavizamientos locales (como loess), por ejemplo:

  • Considera el error de estimación de cada encuesta.
  • Cuando distintas casas publican a frecuencias distintas, es importante considerar que esos datos informan tanto la preferencia como el sesgo de la casa encuestadora. Esto implica, por ejemplo, que los encuestadores con encuestas más grandes o con más encuestas no dominan la estimación.
  • Contiene parámetros más apropiados para calibrar las predicciones contra datos de elecciones anteriores (los intervalos deben ser consistentes con los resultados finales de la elección), incluyendo efectos de casa, sesgos generales, y rapidez en la evolución del sistema.

12.5 Contrafactuales de impacto causal

Los modelos de espacio de estados también presentan una herramienta útil para hacer inferencia causal, específicamente cuando nos interesa el efecto de una intervención en una métrica que se mide en el tiempo.

En un ejemplo anterior, vimos cómo utilizar estos modelos, y variables dummy, para hacer análisis de efecto de intervenciones (efecto de ley de cinturones de seguridad). La hipótesis básica es que no existen puertas traseras una vez que condicionamos a las covariables incluidas. Esto sucedería si alguna variable \(U_t\) afecta a la variable de intervención \(X_t\) al mismo tiempo que afecta el estado del sistema \(\theta_t\) o sus valores futuros. En este caso, el coeficiente de la variable \(X_t\) puede estar contaminado con una correlación no causal. Por ejemplo, un camino de puerta trasera podría ser que hay una decisión de implica poner la ley de cinturones y un reglamento de velocidad máxima en autopistas en fechas cercanas.

Igualmente, el conjunto al que condicionamos no debe contener colisionadores que formen una ruta no causal entre la variable intervenida \(X_t\) y el estado del sistema \(\theta_t\). En el caso de los cinturones, por ejemplo, usar como control \(R_t\), el número de personas con heridas menores por accidentes es mala idea, pues es afectado tanto por la ley como por el estado del sistema (o un antecesor del estado).

En ese ejemplo, recaemos en nuestros supuestos de que no existes puertas traseras y en la forma funcional del modelo para hacer la estimación del contrafactual.

12.5.1 Modelos predictivos del contrafactual

Otra forma de abordar el problema es el siguiente (Brodersen et al. (2015)) , ver también Google Causal Impact):

  • Construimos un modelo predictivo para la serie que vamos a intervenir, utilizando solamente variables que sabemos que no serán afectadas por la intervención.
  • Para constrruir este modelo sólo usamos los datos anteriores a la intervención que estamos considerando.
  • Una alternativa es utilizar modelos de espacio de estados, lo cual más adelante nos permite estimar adecuadamente errores de estimación en efectos causales (toman en cuenta la autocorrelación, y la incertidumbre que aumenta conforme el tiempo pasa después de la intervención).
  • Usando este modelo pronosticamos los valores de la serie de interés después de que ocurre la intervención con nuestro modelo pre-intervención. Estos pronósticos, por el supuesto en el primer inciso, constituyen nuestro contrafactual si la intervención no se hubiera aplicado.
  • Comparamos los valores observados de la serie de interés, después de la intervención, con los pronósticos para estimar el efecto causal de la intervención.

Nótese que no es necesario suponer una forma parámétrica para la intervención, podemos estimarla como la diferencia señalada arriba (individualmente en cada periodo o de forma agregada sobre cierto tiempo después de la intervención), y es posible estimar efectos rezagados de la intervención.

12.5.2 Ejemplo 1

Tomamos el siguiente ejemplo del paquete CausalImpact:

library(CausalImpact)
library(bsts)
set.seed(1241)
x <- 100 + arima.sim(model = list(ar = 0.999), n = 100)
x_int <- rep(0, 100)
y <- 1.2 * x + rnorm(100)

Suponemos que la intervencion se hace en el tiempo \(t=71\), y que tiene el efecto de aumentar la \(y\) en 10 unidades:

y[71:100] <- y[71:100] + 10
x_int[71:100] <- 1
datos_tbl <- tibble(y, x, x_int)

Los dos series, antes de la intervención, muestra correlación. Construiremos un

datos_tbl |> mutate(t = row_number()) |> 
  filter(t < 71) |> 
  ggplot(aes(x = t)) +
  geom_line(aes(y = y)) +
  geom_line(aes(y = x), colour = "red")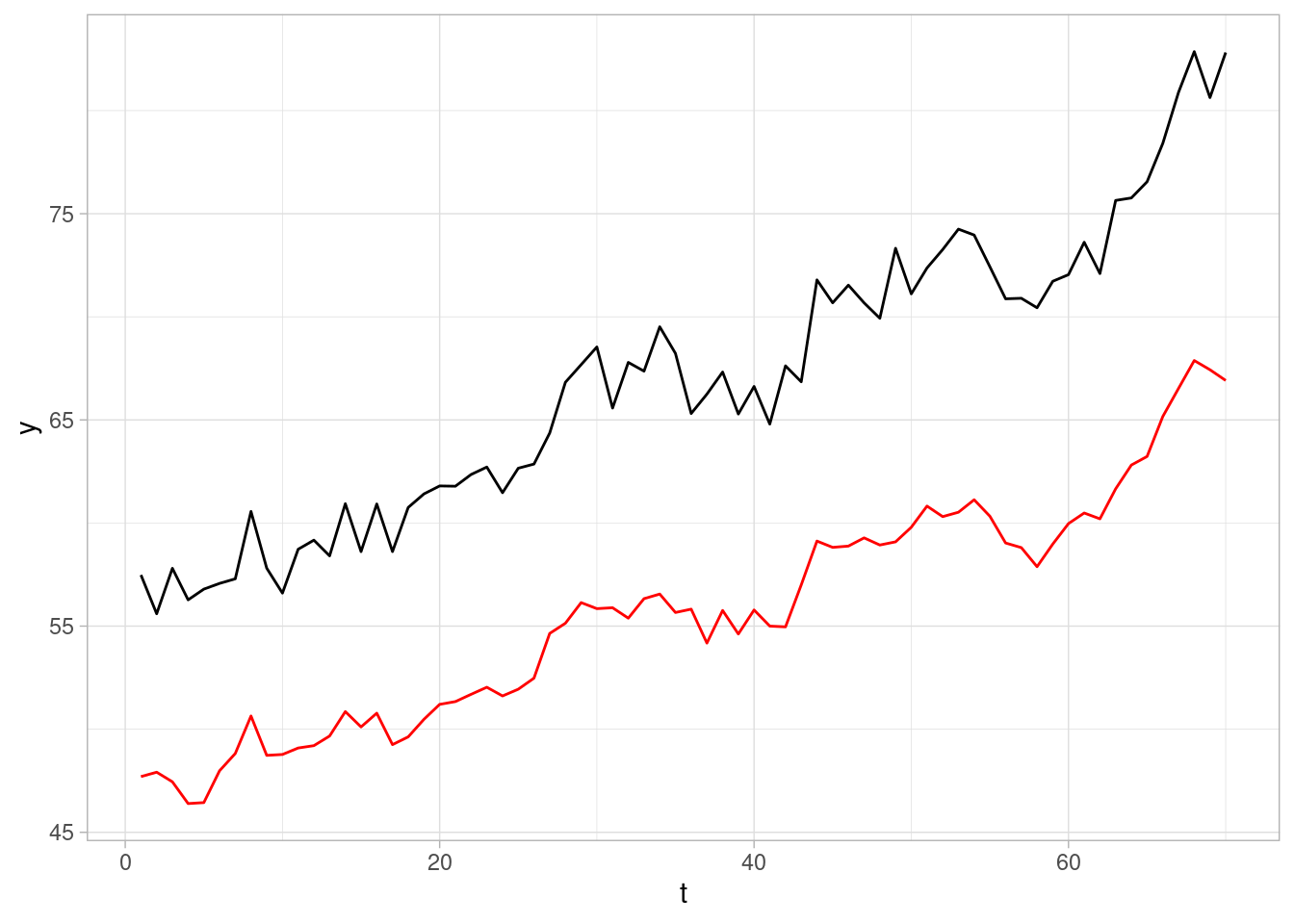

  • Si sabemos que la serie \(x\) roja no puede ser afectada por nuestra intervención sobre \(y\), y suponemos que la relación entre \(y\) y \(x\) se mantendría después del tiempo de la intervención, entonces podemos contruir un modelo predictivo de \(y\) en función de \(x\) para construir contrafactuales.

Un ejemplo es: si imaginamos que una promoción se hace exclusivamente en una región \(A\) del país, podemos usar otras regiones del país como predictores de las ventas en la región \(A\). Muchas veces estos modelos tienden a ser más precisos y simples pues no es necesario incluir factores como estacionalidad, pues están sujetos a fuentes de variación similares.

En términos de contrafactuales: una vez que construimos este modelo, hacemos pronósticos con nuestro modelo para \(t>t_{int}\), después de la intervención, que denotamos como \(\hat{y}_t^0\), que son estimaciones de \(y_t^0\) (el contrafactual sin la intervención). Después de la intervención observamos \(y_t^1\), así que calculamos, para cada \(t\):

\[y_t^1 - \hat{y}_t^0\] Esta cantidad tiene una distribución posterior, que representa lo que sabemos del efecto causal individual sobre la región tratada \(A\).

Método de Impacto causal

Requerimos los siguientes supuestos fuertes:

  • La serie de interés \(y\) puede ser explicada en términos de otras series de tiempo que no son afectadas por la intervención.
  • La relación entre la serie de interés \(y\) y la serie de control se supone estable durante el periodo post-intervención.

Ejemplo

Usamos la idea de construir un contrafactual con el método de impacto causal:

En primer lugar, excluímos los datos post-tratamiento:

post_periodo <- c(71, 100)
y_mod <- y
post_y <- y[post_periodo[1] : post_periodo[2]]
y_mod[post_periodo[1] : post_periodo[2]] <- NA

Construimos un modelo. En este caso usamos regresión estática pero agregamos una componente de nivel local:

set.seed(886)
mod_esp_1 <- AddLocalLevel(list(), y_mod)
mod_esp_2 <- AddLocalLinearTrend(list(), y_mod)
ajuste_pre_1 <- bsts(y_mod ~ x, mod_esp_1, niter = 25000, ping = 5000)
=-=-=-=-= Iteration 0 Wed May 15 13:49:24 2024 =-=-=-=-=
=-=-=-=-= Iteration 5000 Wed May 15 13:49:26 2024 =-=-=-=-=
=-=-=-=-= Iteration 10000 Wed May 15 13:49:28 2024 =-=-=-=-=
=-=-=-=-= Iteration 15000 Wed May 15 13:49:30 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Wed May 15 13:49:32 2024 =-=-=-=-=
ajuste_pre_2 <- bsts(y_mod ~ x, mod_esp_2, niter = 25000, ping = 5000)
=-=-=-=-= Iteration 0 Wed May 15 13:49:34 2024 =-=-=-=-=
=-=-=-=-= Iteration 5000 Wed May 15 13:49:36 2024 =-=-=-=-=
=-=-=-=-= Iteration 10000 Wed May 15 13:49:38 2024 =-=-=-=-=
=-=-=-=-= Iteration 15000 Wed May 15 13:49:41 2024 =-=-=-=-=
=-=-=-=-= Iteration 20000 Wed May 15 13:49:43 2024 =-=-=-=-=
CompareBstsModels(list(ajuste_pre_1, ajuste_pre_2))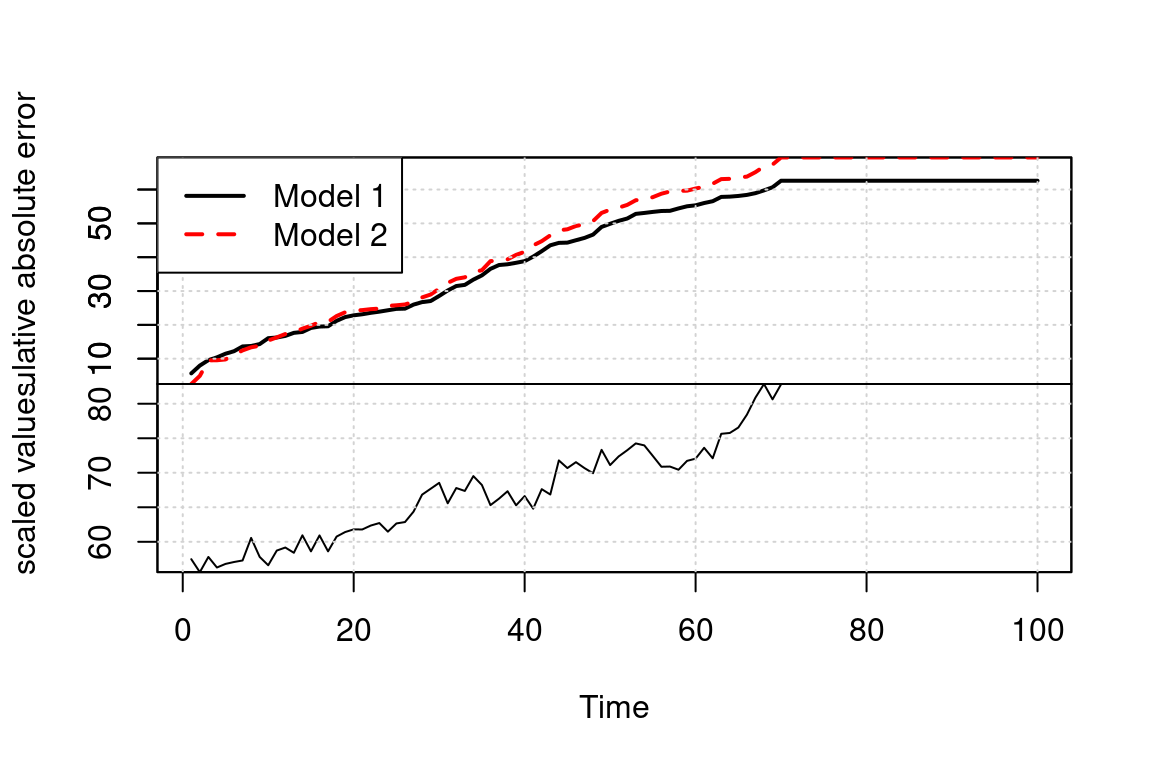

Seleccionamos el primer modelo:

plot(ajuste_pre_1)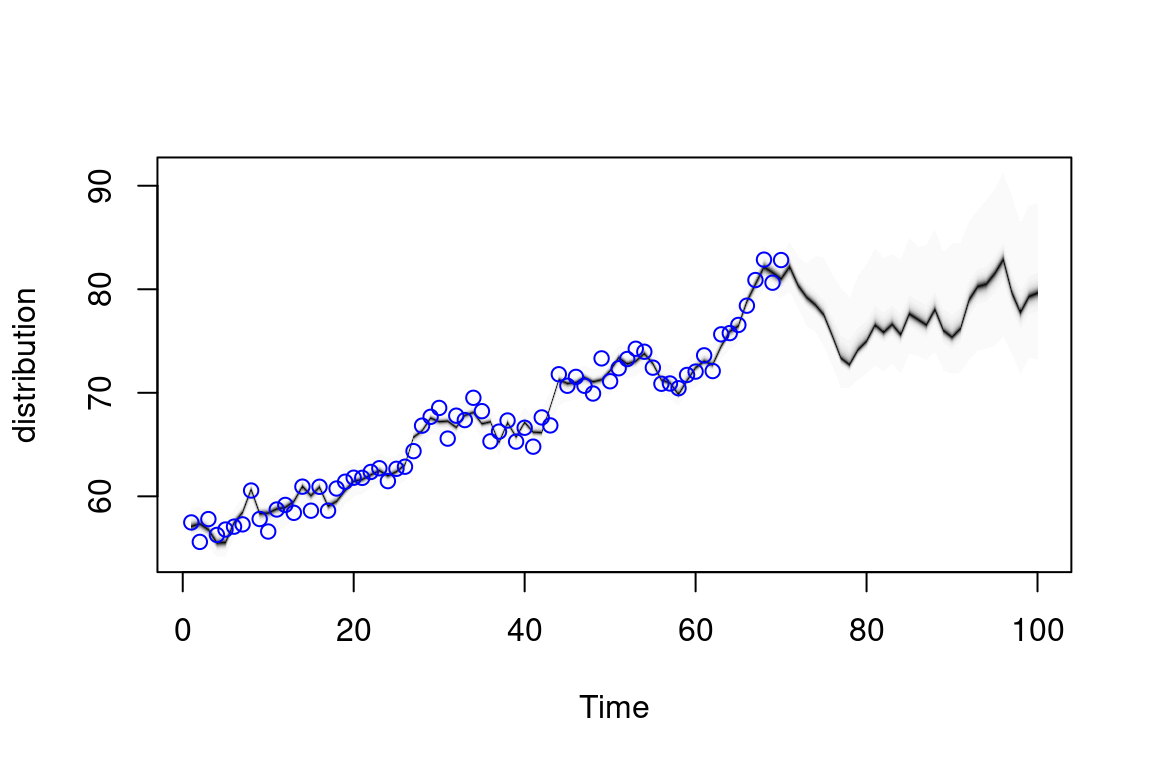

plot(ajuste_pre_1, "components")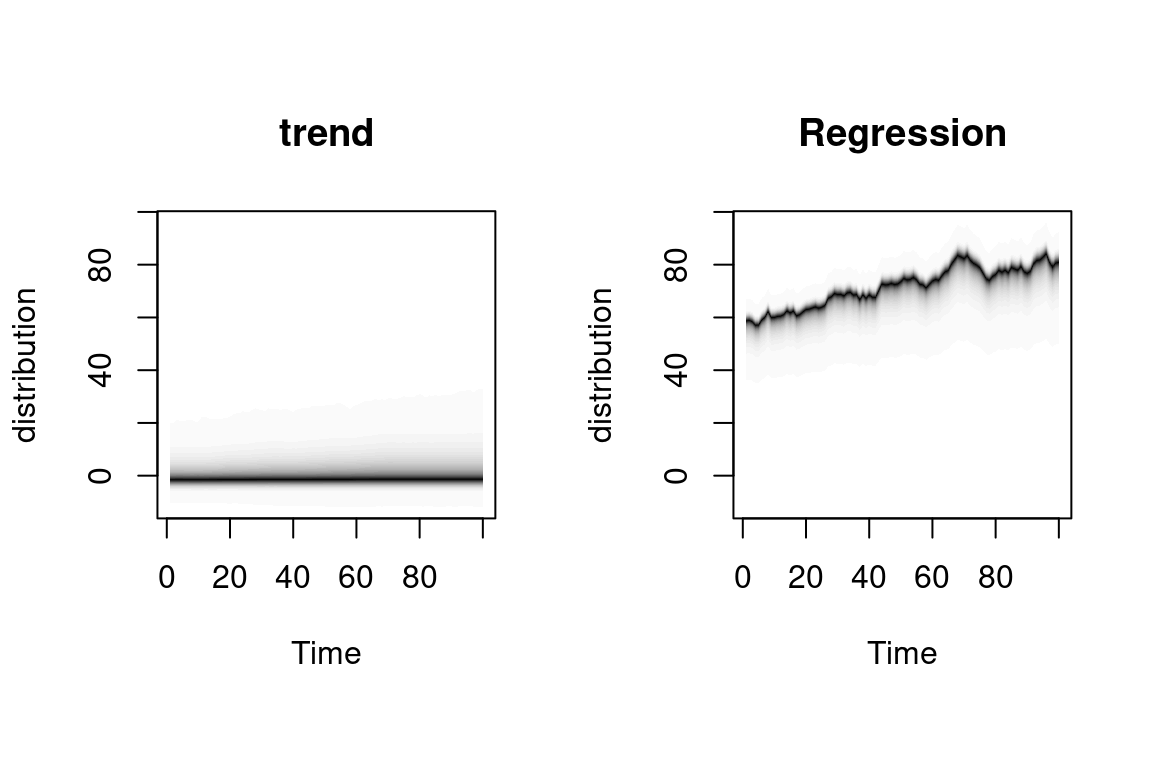

Extraemos predicciones que automáticamente hace bsts

# quitar burn-in
estado_contrib <- ajuste_pre_1$state.contributions[-seq_len(500), , ,drop = FALSE]
# sumar contribuciones de componentes
pred_cf <- rowSums(aperm(estado_contrib, c(1, 3, 2)), dims = 2)
# extraer period post-intervencion
pred_cf <- pred_cf[, 71:100]
dim(pred_cf)
[1] 24500    30

Y estimamos el efecto promedio en estos 30 días utilizando el valor observado de \(y\) menos las simulaciones correspondientes del contrafactual:

media_dia_post <- apply(pred_cf, 1, mean)
diferencia <-  mean(y[71:100]) - media_dia_post
mean(diferencia)
[1] 9.396539
quantile(diferencia, c(0.025, 0.975)) |> round(3)
  2.5%  97.5% 
 8.342 10.211

O más simplemente:

CausalImpact(bsts.model = ajuste_pre_1,
                       post.period.response = y[71:100])
Posterior inference {CausalImpact}

                         Average       Cumulative   
Actual                   87            2613         
Prediction (s.d.)        78 (0.53)     2331 (15.89) 
95% CI                   [77, 79]      [2304, 2364] 
                                                    
Absolute effect (s.d.)   9.4 (0.53)    281.9 (15.89)
95% CI                   [8.3, 10]     [248.9, 310] 
                                                    
Relative effect (s.d.)   12% (0.76%)   12% (0.76%)  
95% CI                   [11%, 13%]    [11%, 13%]   

Posterior tail-area probability p:   4e-05
Posterior prob. of a causal effect:  99.9959%

For more details, type: summary(impact, "report")

Podemos hacer esto automáticamente usando funciones del paquete:

pre_periodo <- c(1, 70)
post_periodo <- c(71, 100)
impact <- CausalImpact(datos_tbl |> select(y, x), 
  pre_periodo, post_periodo, model.args = list(niter = 5000))
plot(impact)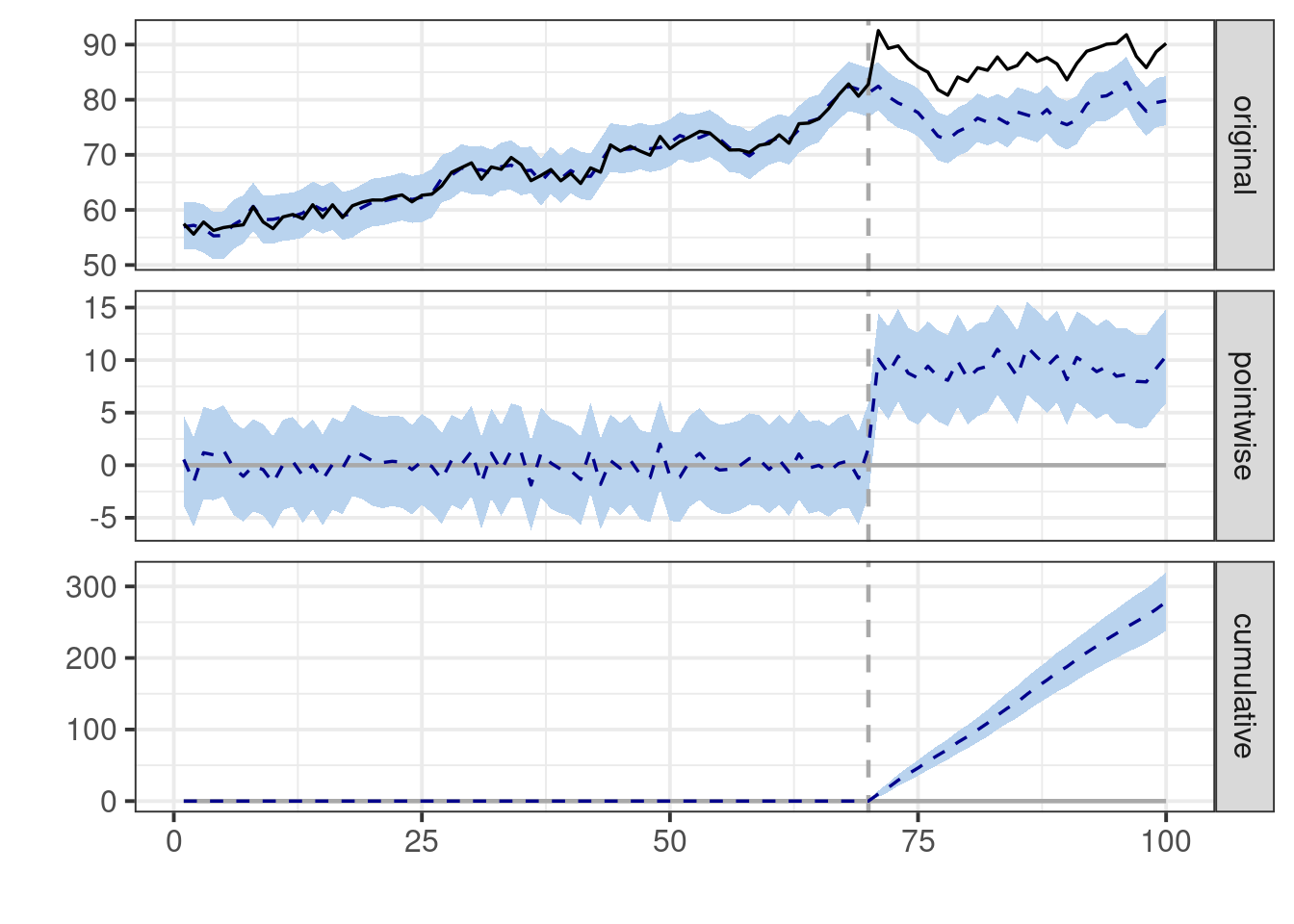

summary(impact)
Posterior inference {CausalImpact}

                         Average      Cumulative   
Actual                   87           2613         
Prediction (s.d.)        78 (0.69)    2335 (20.75) 
95% CI                   [76, 79]     [2294, 2375] 
                                                   
Absolute effect (s.d.)   9.3 (0.69)   278.5 (20.75)
95% CI                   [7.9, 11]    [238.0, 320] 
                                                   
Relative effect (s.d.)   12% (1%)     12% (1%)     
95% CI                   [10%, 14%]   [10%, 14%]   

Posterior tail-area probability p:   2e-04
Posterior prob. of a causal effect:  99.97997%

For more details, type: summary(impact, "report")

Ejemplo 2

Nótese adicionalmente esta estimación es no-paramétrica, y no establecemos un modelo explícito para el efecto de la intervención.

library(CausalImpact)
library(bsts)
set.seed(461)
x <- 100 + arima.sim(model = list(ar = 0.999), n = 100)
x_int <- rep(0, 100)
y <- 1.2 * x + rnorm(100)
y[71:100] <- y[71:100] + 5 * (71:100 - 71) * exp(-25 * (71:100 -71) /100)
x_int[71:100] <- 1
datos_tbl <- tibble(y, x, x_int)
pre_period <- c(1, 70)
post_period <- c(71, 100)
impact <- CausalImpact(datos_tbl |> select(y, x), pre_period, post_period)
plot(impact)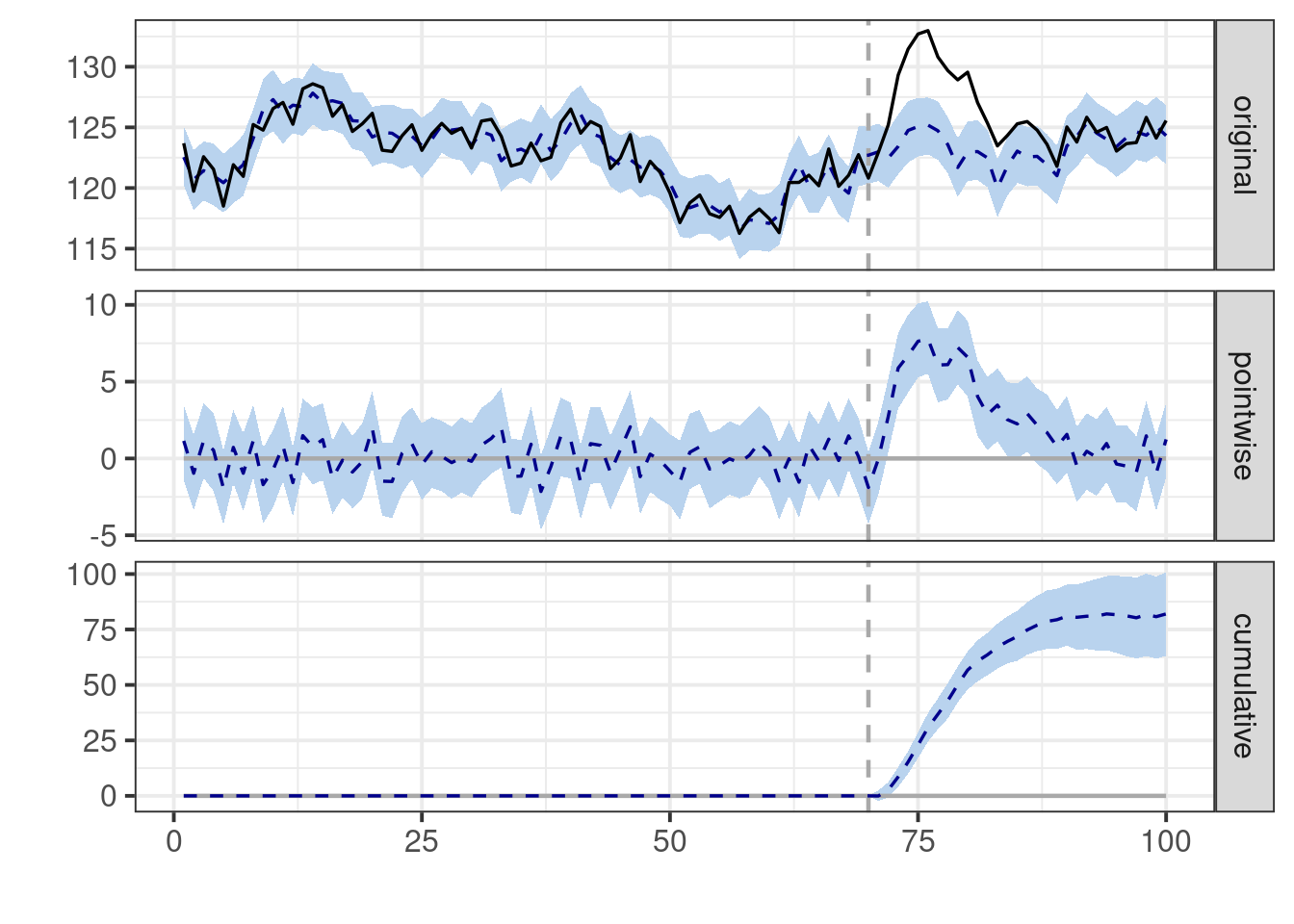

En casos como este, muchas veces tiene más sentido considerar el efecto acumulado en lugar del promedio (por ejemplo si la variable \(y\) son clicks o compras):

summary(impact)
Posterior inference {CausalImpact}

                         Average        Cumulative   
Actual                   126            3785         
Prediction (s.d.)        123 (0.32)     3703 (9.75)  
95% CI                   [123, 124]     [3684, 3722] 
                                                     
Absolute effect (s.d.)   2.7 (0.32)     82.0 (9.75)  
95% CI                   [2.1, 3.4]     [63.1, 100.8]
                                                     
Relative effect (s.d.)   2.2% (0.27%)   2.2% (0.27%) 
95% CI                   [1.7%, 2.7%]   [1.7%, 2.7%] 

Posterior tail-area probability p:   0.00101
Posterior prob. of a causal effect:  99.8993%

For more details, type: summary(impact, "report")

12.6 Ejemplo: cinturones de seguridad

En el ejemplo de cinturones de seguridad, es necesario encontrar series que se razonable que no son afectadas por la introducción de la ley de cinturones de seguridad.

Supondremos (aunque puede ser discutible), que la ley no tendrá un efecto considerable en kilómetros recorridos o precio de la gasolina, y tampoco tendrá un efecto sobre pasajeros que viajan en los asientos traseros. Estas variables son candidatas para construir un modelo predictivo antes de la introducción de la ley.

uk_drivers <- Seatbelts |> as_tibble() |>  
  mutate(ind = row_number()) 
pre_periodo <- c(1, which(uk_drivers$law == 0) |> max())
pre_periodo
[1]   1 169
post_periodo <- c(pre_periodo[2] + 1, nrow(uk_drivers))
datos_mod_tbl <- uk_drivers |> select(drivers, kms, rear, PetrolPrice,ind)

Podemos construir nuestro modelo manualmente (usualmente, varios modelo que comparamos en capacidad predictiva y calibración de intervalos):

datos_ent_tbl <- datos_mod_tbl
datos_ent_tbl <- datos_mod_tbl |> filter(ind <= 140)
modelo_ent  <- AddLocalLevel(list(),
    sigma.prior = SdPrior(5, 10),
    y = datos_ent_tbl$drivers) |> 
  AddSeasonal(nseasons = 12, datos_ent_tbl$drivers)
ajuste_ent <- bsts(drivers ~ kms + rear + PetrolPrice, 
                 modelo_ent, data = datos_ent_tbl,
                 niter = 5000, ping = 5000)
=-=-=-=-= Iteration 0 Wed May 15 13:49:51 2024 =-=-=-=-=
plot(ajuste_ent)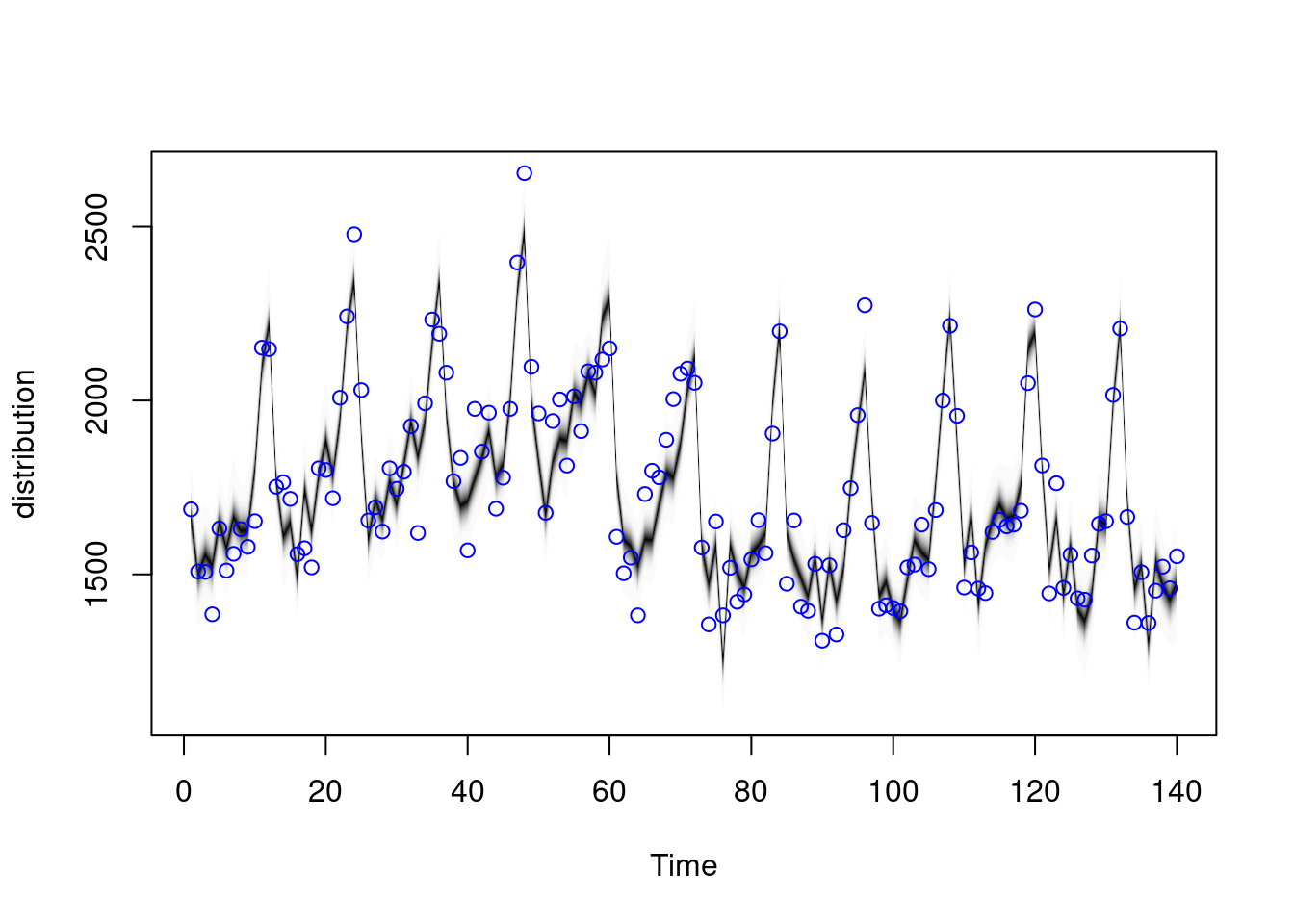

Checamos predicciones con un periodo de validación hasta antes de la intervención:

preds_val <- predict(ajuste_ent, newdata = datos_mod_tbl |> 
          filter(ind > 140, ind < 169)) 
drivers_val <- datos_mod_tbl |> 
          filter(ind > 140, ind < 169) |> pull(drivers)
tibble(pred = preds_val$mean, 
       pred_inf = preds_val$interval[1, ],
       pred_sup = preds_val$interval[2, ],
       drivers = drivers_val) |> 
  ggplot(aes(x = drivers, y = pred, ymin = pred_inf,ymax = pred_sup )) + geom_point() + geom_linerange(colour = "red") + 
  geom_abline() + coord_fixed()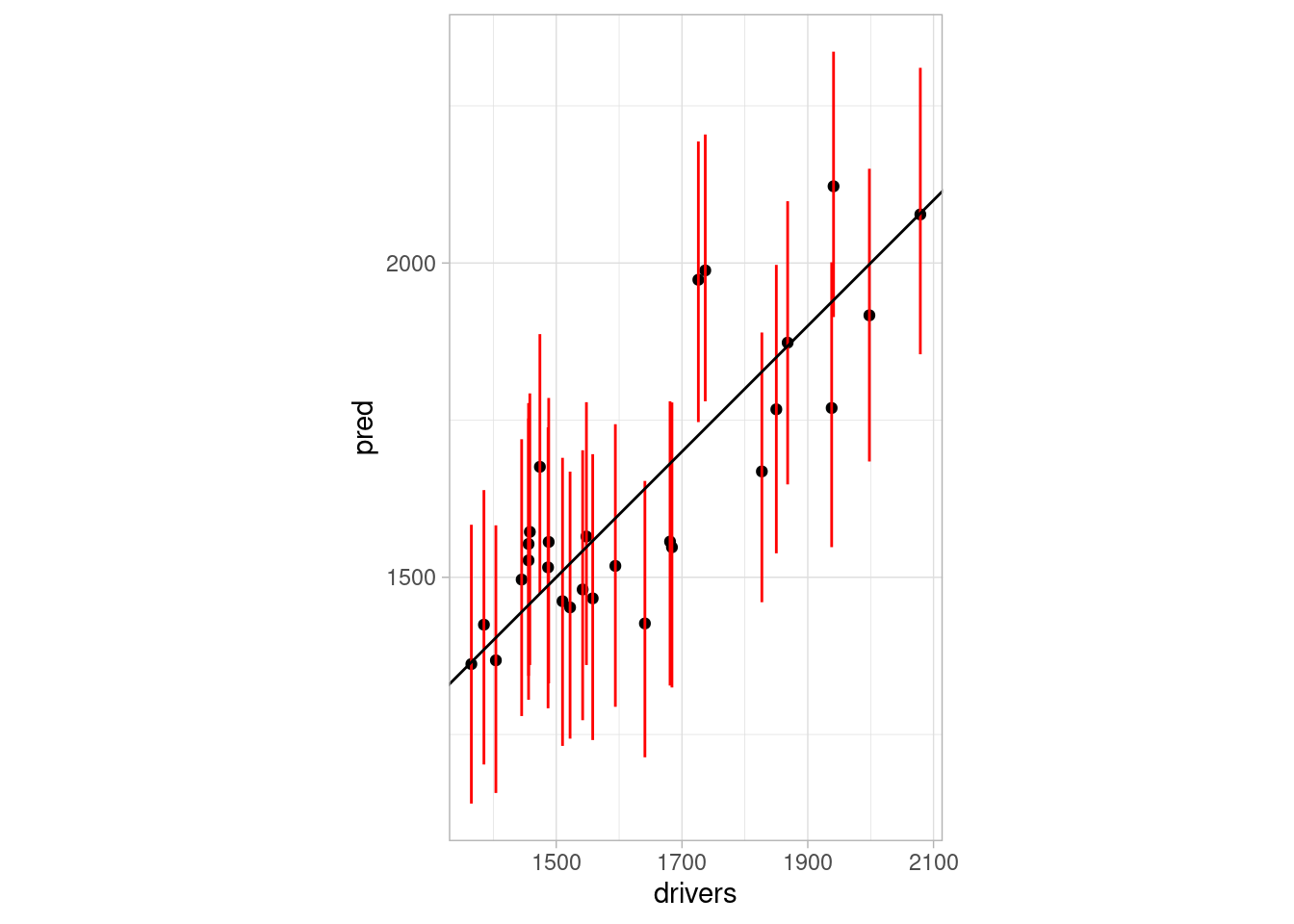

# MAPE
mean(abs(preds_val$mean - drivers_val)/drivers_val)
[1] 0.05900544

Estas son las variables que utilizamos en el modelo (el color indica el signo cuando entra en el modelo):

plot(ajuste_ent, "coefficients")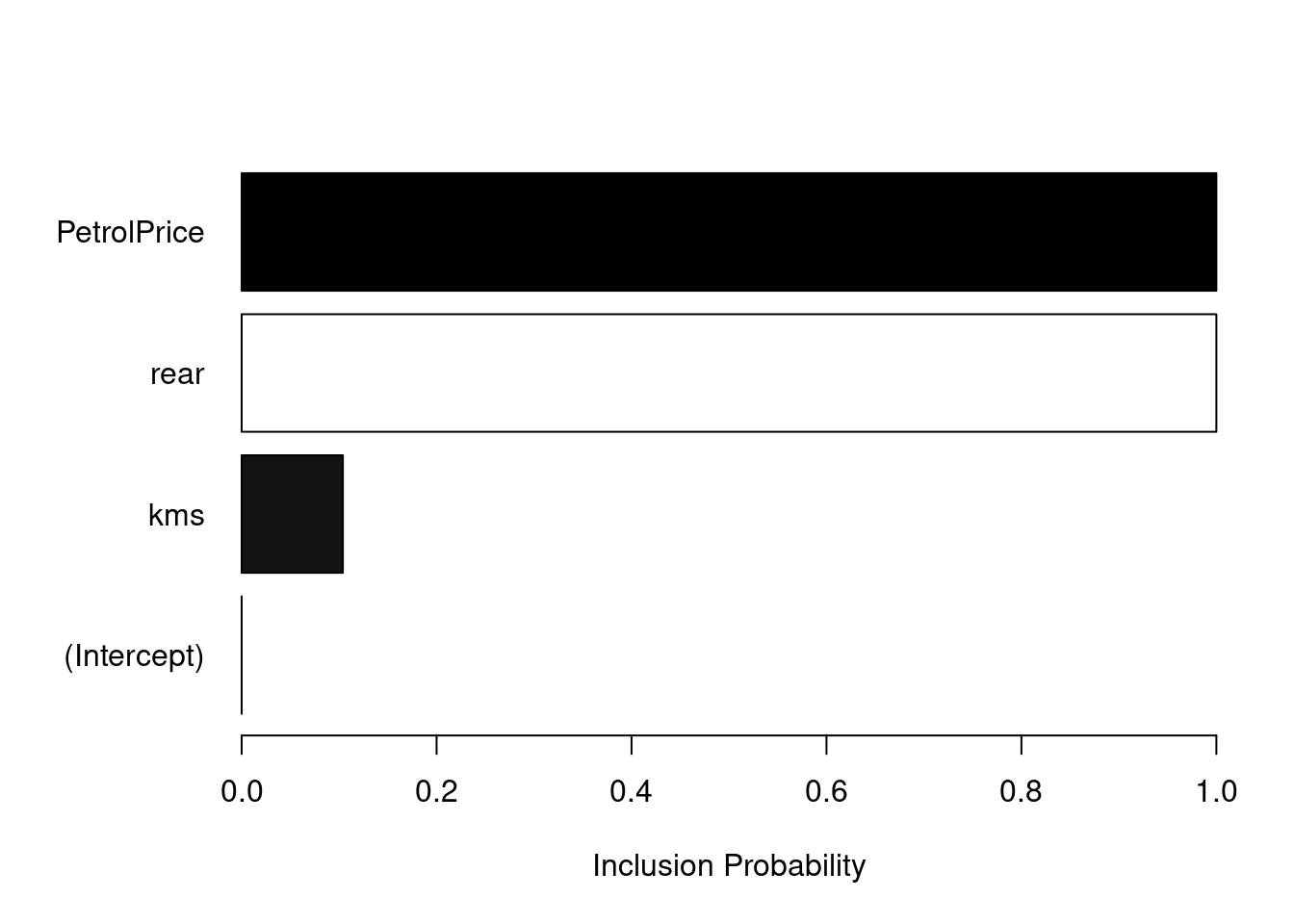

Y ahora ajustamos el modelo a todos los datos pre intervención:

datos_mod_tbl$y <- datos_mod_tbl$drivers
datos_mod_tbl$y[post_periodo[1]:post_periodo[2]] <- NA
modelo_1  <- AddLocalLevel(list(), 
    sigma.prior = SdPrior(5, 10),
    datos_mod_tbl$y) |> 
  AddSeasonal(nseasons = 12, datos_mod_tbl$y)
ajuste_1 <- bsts(y ~ kms + rear + PetrolPrice, modelo_1, data = datos_mod_tbl,
                   niter = 5000, ping = 5000)
=-=-=-=-= Iteration 0 Wed May 15 13:50:00 2024 =-=-=-=-=
impacto <- CausalImpact(bsts.model = ajuste_1,
      post.period.response = 
        datos_mod_tbl$drivers[post_periodo[1]:post_periodo[2]])
plot(impacto)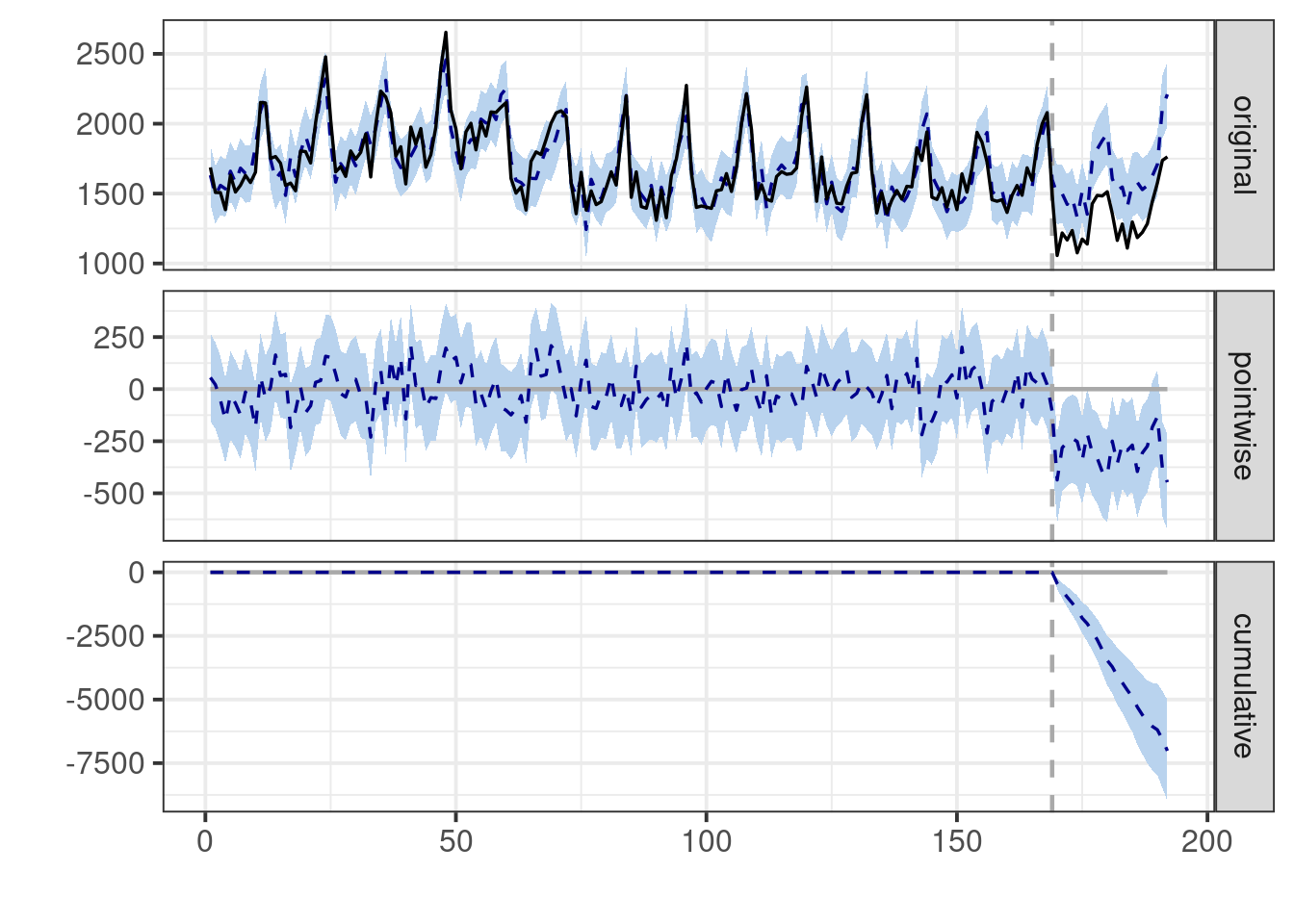

impacto
Posterior inference {CausalImpact}

                         Average        Cumulative    
Actual                   1322           30399         
Prediction (s.d.)        1627 (43)      37414 (995)   
95% CI                   [1540, 1713]   [35412, 39390]
                                                      
Absolute effect (s.d.)   -305 (43)      -7015 (995)   
95% CI                   [-391, -218]   [-8991, -5013]
                                                      
Relative effect (s.d.)   -19% (2.2%)    -19% (2.2%)   
95% CI                   [-23%, -14%]   [-23%, -14%]  

Posterior tail-area probability p:   0.00022
Posterior prob. of a causal effect:  99.97838%

For more details, type: summary(impact, "report")

Finalmente, podemos checar cómo cambiaron las variables del modelo predictivo post-entrenamiento. Por ejemplo, para las muertes y heridas graves de pasajeros de los asientos traseros:

uk_drivers |> 
  ggplot(aes(x = ind)) +
  geom_line(aes(y = drivers)) +
  geom_line(aes(y = rear), colour = "red")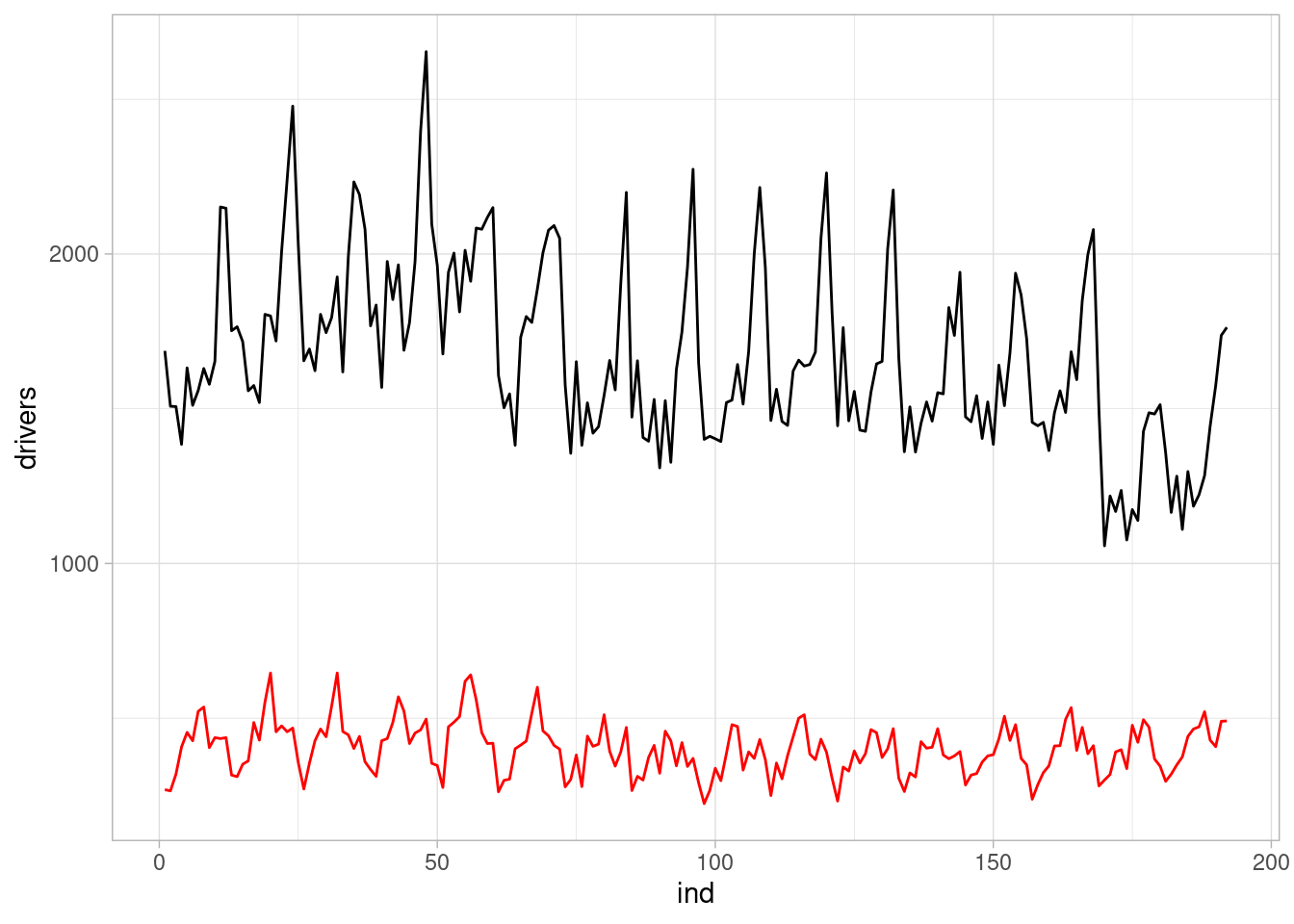

O más simplemente, podemos usar los defaults de CausalImpact:

impacto_auto <- CausalImpact(datos_mod_tbl |> select(-y), pre_periodo, post_periodo)
impacto_auto
Posterior inference {CausalImpact}

                         Average        Cumulative    
Actual                   1322           30399         
Prediction (s.d.)        1610 (45)      37036 (1043)  
95% CI                   [1524, 1697]   [35061, 39034]
                                                      
Absolute effect (s.d.)   -289 (45)      -6637 (1043)  
95% CI                   [-375, -203]   [-8635, -4662]
                                                      
Relative effect (s.d.)   -18% (2.3%)    -18% (2.3%)   
95% CI                   [-22%, -13%]   [-22%, -13%]  

Posterior tail-area probability p:   0.00101
Posterior prob. of a causal effect:  99.8995%

For more details, type: summary(impact, "report")

Nota: los valores de las iniciales que usa por default CausalImpact son diferentes a los de bsts.

Brodersen, Kay H., Fabian Gallusser, Jim Koehler, Nicolas Remy, y Steven L. Scott. 2015. «Inferring causal impact using Bayesian structural time-series models». Annals of Applied Statistics 9: 247-74.
Durbin, J., y S. J. Koopman. 2001. Time Series Analysis by State Space Methods. Oxford Statistical Science Series. Clarendon Press. https://books.google.com.mx/books?id=XRCu5iSz\_HwC.
Hyndman, R. J., y G. Athanasopoulos. 2014. Forecasting: principles and practice. OTexts. https://books.google.com.mx/books?id=gDuRBAAAQBAJ.
Scott, Steven L., y Hal R. Varian. 2015. Bayesian Variable Selection for Nowcasting Economic Time Series. University of Chicago Press. https://doi.org/10.7208/chicago/9780226206981.003.0004.