8  Markov Chain Monte Carlo

library(tidyverse)
library(kableExtra)
library(DiagrammeR)
ggplot2::theme_set(ggplot2::theme_light())
inv_logit <- \(x) 1 / (1 + exp(-x)) 

En esta sección exlicaremos brevemente cómo funcionan paquetes como Stan para producir simulaciones de una posteriores complicadas en dimensión alta.

En primer lugar, recordemos que si queremos calcular la posterior de un modelo (generalmente para calcular después resúmenes que involucran integrales de esta posterior) tenemos los siguiente enfoques:

1. Intentar hacer los cálculos analíticamente.
2. Usar una aproximación de rejilla.
3. Simulación por Markov Chain Monte Carlo (MCMC).

Stan utiliza 3, y hay variedad de algoritmos MCMC. Ya discutimos que 1, la aproximación analítica, es en general imposible (a menos fuera de ciertos modelos restringidos). La aproximación 2 excesivamente intensiva, al grado que sólo para modelos muy chicos y con pocos parámetros es posible utilizarla. Existen otros métodos también como aproximaciones cuadráticas que en ciertos casos funcionan, pero son limitados en su aplicación.

La idea de simulación de variables aleatorias es ahora fundamental en muchas áreas científicas, incluyendo la estadística, y los métodos que la utilizan se llaman métodos de Monte Carlo. Por ejemplo, considera el método bootstrap, pruebas de permutaciones, validación cruzada, y en general simulación para cálculo de resúmenes que son difíciles de calcular directamente (por ejemplo, la mediana de una distribución Gamma, ver Median approximations and bounds aquí).

8.1 Algoritmos Metropolis-Hastings

Uno de los primeros algoritmos MCMC fue el de Metropolis-Hastings, que veremos primero en algunos ejemplos. Veremos también por qué ahora tenemos mejores opciones que MH para estimar posteriores de nuestros modelos.

Ejemplo: dos implementaciones de Metropolis

Supongamos que queremos simular de una variable aleatoria \(X\) con distribución discreta sobre los valores \(1,2\ldots, k\) con probabilidades \(p(1),p(2),\ldots,p(k)\). Este problema puede resolverse fácilmente de varias maneras, pero utilizaremos un método de Monte Carlo tipo Metropolis. Supongamos que podemos simular de una variable aleatoria \(U\) que es uniforme en \(1,2,\ldots, k\) (con probabilidades iguales a 1/k).

Lo que podemos hacer es lo que sigue, para \(i=1,\ldots, M\):

0. Para \(i=1\), comenzamos fijando un valor \(x_1\) en \(1,2,\ldots, k\).

Para cada \(i\),

2. Simulamos una uniforme en \(1,2,\ldots, k\). Al valor \(u_i\) obtenido le llamamos valor propuesto.
3. Calculamos \(q = p(u_i)/p(x_i)\) (el cociente de la probabilidad del valor propuesto entre la probabilidad del valor actualo).
4. Si \(q > 1\), aceptamos el valor propuesto y ponemos \(x_{i+1} = u_i\).
5. Si \(q < 1\), aceptamos el valor propuesto con probabilidad \(q\) (\(x_{i+1} = u_i\)), y con probabilidad \(1-q\) rechazamos (\(x_{i+1} = x_i\)).

El resultado es una sucesión de valores \(x_1,x_2,\ldots, x_M\). Es posible demostrar que la distribución de estas \(x_i\) converge a la distribución \(p(1),\ldots, p(k)\) si \(M\) es suficientemente grande.

Este método se llama Metropolis-Hastings. Es un método de Monte Carlo, y como podemos ver, se trata de una cadena de Markov, pues la distribución cada siguiente lugar \(x_{i+1}\), condicionada al valor actual \(x_i\) no depende de valores anteriores de las \(x\).

set.seed(45123)
# definimos estas p
k <- 40
p <- exp(-(1:k - k/3)^2 / 10)
p <- p /sum(p)
dist_obj <- tibble(x = 1:k, p = p)
# simulamos
M <- 200000
x <- numeric(M)
x[1] <- 20
for(i in 1:M){
  u <- sample(1:k, 1)
  q <- p[u] / p[x[i]]
  if(runif(1) < q){
    x[i+1] <- u
  } else {
    x[i+1] <- x[i]  
  }
}

En rojo mostramos las probabilidades objetivo que queremos estimar, y en negro las estimadas con nuestro método de arriba.

resultados_sim <- tibble(x = x) |> 
  mutate(n_sim = row_number())
resumen_sim <- resultados_sim |> count(x) |> 
  right_join(tibble(x = 1:k, p = p)) |> 
  mutate(n = ifelse(is.na(n), 0, n)) |> 
  mutate(p_aprox = n / sum(n))

Joining with `by = join_by(x)`

ggplot(dist_obj, aes(x = x)) +
    geom_point(aes(y = p)) +
  geom_point(data = resumen_sim, 
             aes(y = p_aprox), color = "red", size = 3, alpha = 0.5)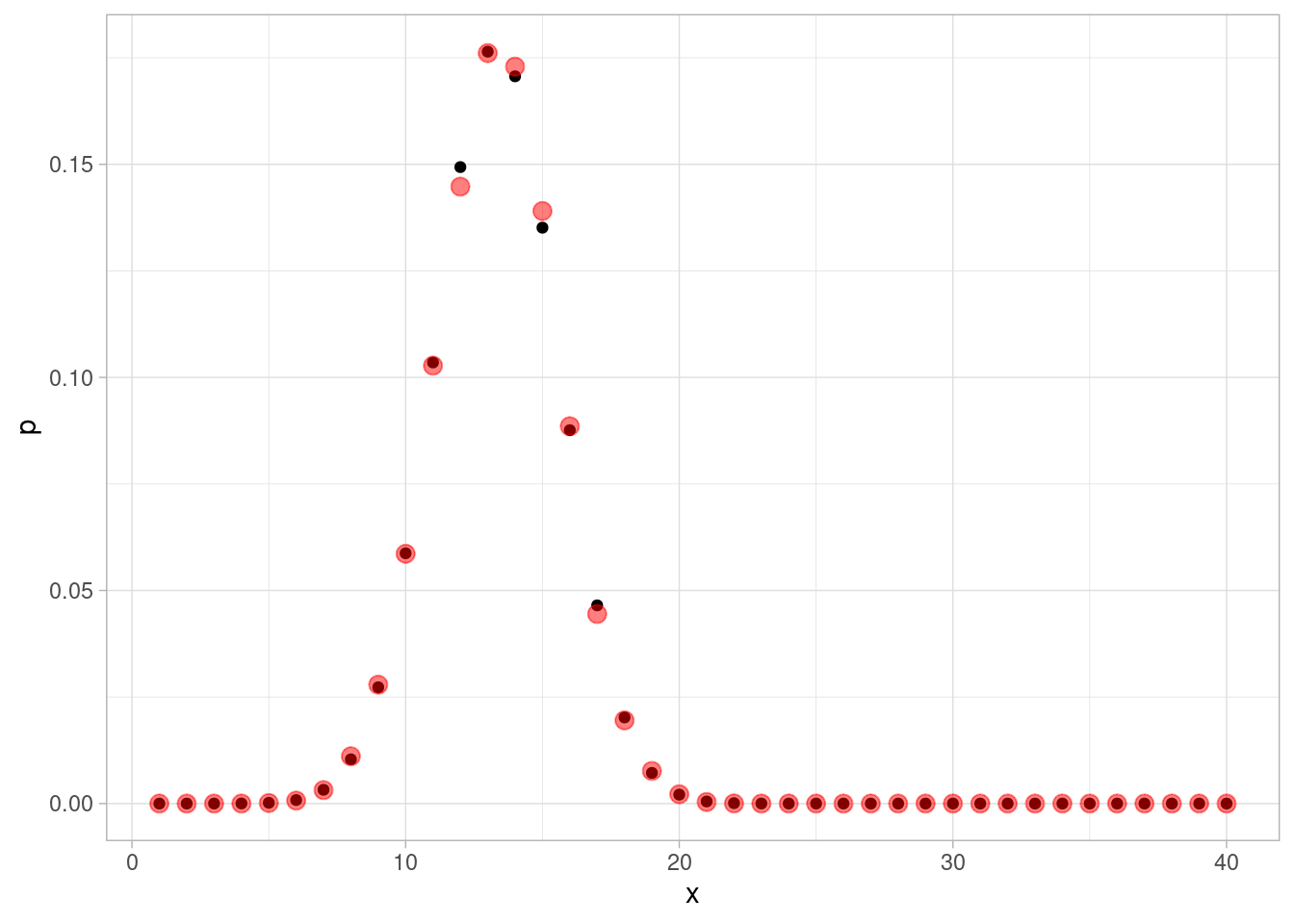 

Como vemos, los valores de \(x_1,\ldots, x_M\) se distribuyen aproximadamente como la distribución \(p\) objetivo. Esta es una manera de simular valores de esta distribución discreta \(p\). Podemos ver cómo se ven las simulaciones sucesivas:

ggplot(resultados_sim |> filter(n_sim < 400), aes(x = n_sim, y = x)) +
  geom_line() + scale_y_continuous(breaks = 1:20)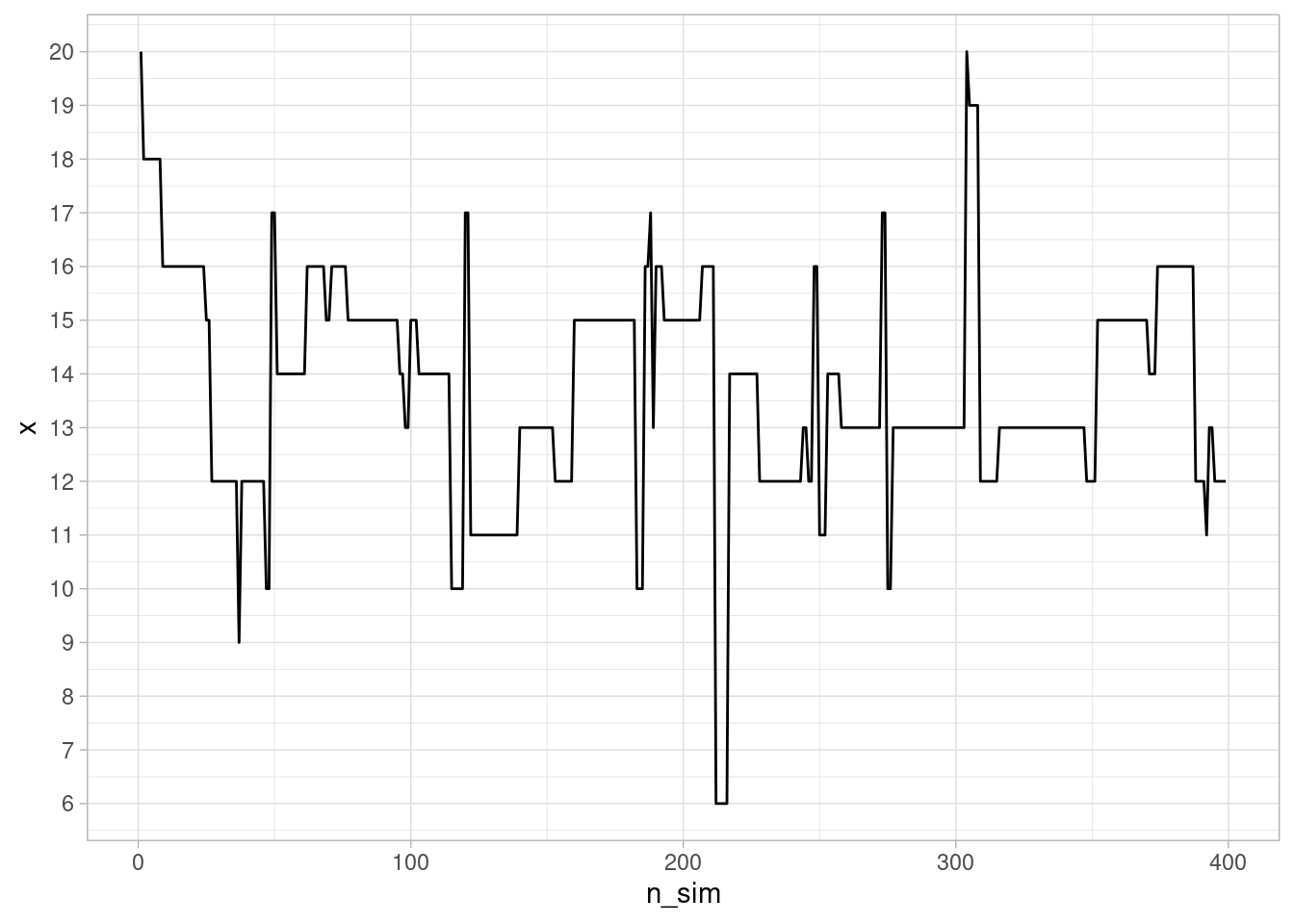

El defecto que tiene este algoritmo es que puede ser relativamente lento, pues vemos que hay periodos largos donde se “atora” en valores de probabilidad relativamente alta. La razón es que en muchos pasos, estamos proponiendo “saltos al vacío” a lugares de probabilidad muy baja, que rara vez se aceptan.

Podemos hacer más eficiente nuestro algoritmo si le permitimos explorar con mayor facilidad los posibles valores de \(x\). Esto se logra proponiendo saltos locales: si estamos en \(x_i\), entonces proponemos los valores \(x_i - 1\) y \(x_i + 1\) con la misma probabilidad 1/2 (excepto en los extremos donde sólo proponemos \(x_i,x_i+1\) o \(x_i-1,x_i\)).

Proponemos entonces la suguiente modificación del paso 1 de propuesta:

0. Para \(i=1\), comenzamos fijando un valor \(x_1\) en \(1,2,\ldots, k\).

Para cada \(i\),

2. Si \(1< x_i<k\), escogemos al azar un salto a la derecha o al izquierda con igual probabilidad 1/2. En los extremos \(x_i=1\) o \(x_i=k\) escogemos entre \(1,2\) o \(k-1,k\) respectivamente. Al valor \(u_i\) obtenido le llamamos valor propuesto.
3. Calculamos \(q = p(u_i)/p(x_i)\) .
4. Si \(q > 1\), aceptamos el valor propuesto y ponemos \(x_{i+1} = u_i\).
5. Si \(q < 1\), aceptamos el valor propuesto con probabilidad \(q\) (\(x_{i+1} = u_i\)), y con probabilidad \(q\) rechazamos(\(x_{i+1} = x_i\)).

Esto lo escribimos como sigue:

#set.seed(4511)
# simulamos
x <- numeric(M)
x[1] <- 20
for(i in 1:M){
  u <- sample(c(x[i] - 1,  x[i] + 1), 1)
  if(u == k+1) u <- k
  if(u == 0) u <- 1
  q <- p[u] / p[x[i]]
  if(runif(1) < q){
    x[i+1] <- u
  } else {
    x[i+1] <- x[i]  
  }
}

Obtenemos:

resultados_sim_2 <- tibble(x = x) |> 
  mutate(n_sim = row_number())
resumen_sim_2 <- resultados_sim_2 |> count(x) |> 
  mutate(p_aprox = n / sum(n))
ggplot(dist_obj, aes(x = x)) +
    geom_point(aes(y = p)) +
  geom_point(data = resumen_sim_2, 
             aes(y = p_aprox), color = "red", size = 3, alpha = 0.5)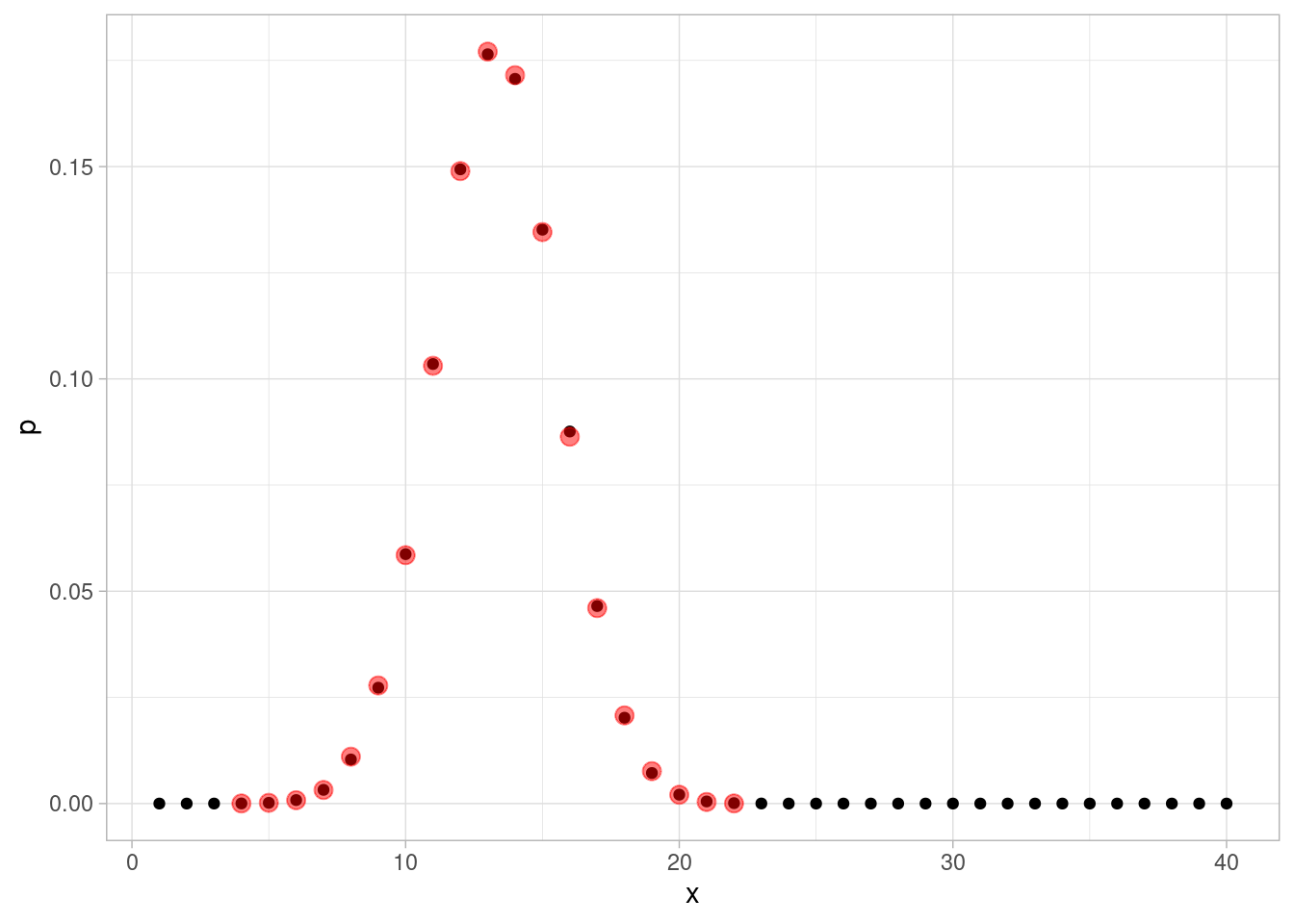 

Y podemos ver cómo evoluciona nuestra cadena de Markov:

ggplot(resultados_sim_2 |> filter(n_sim < 400), aes(x = n_sim, y = x)) +
  geom_line() + scale_y_continuous(breaks = 1:20)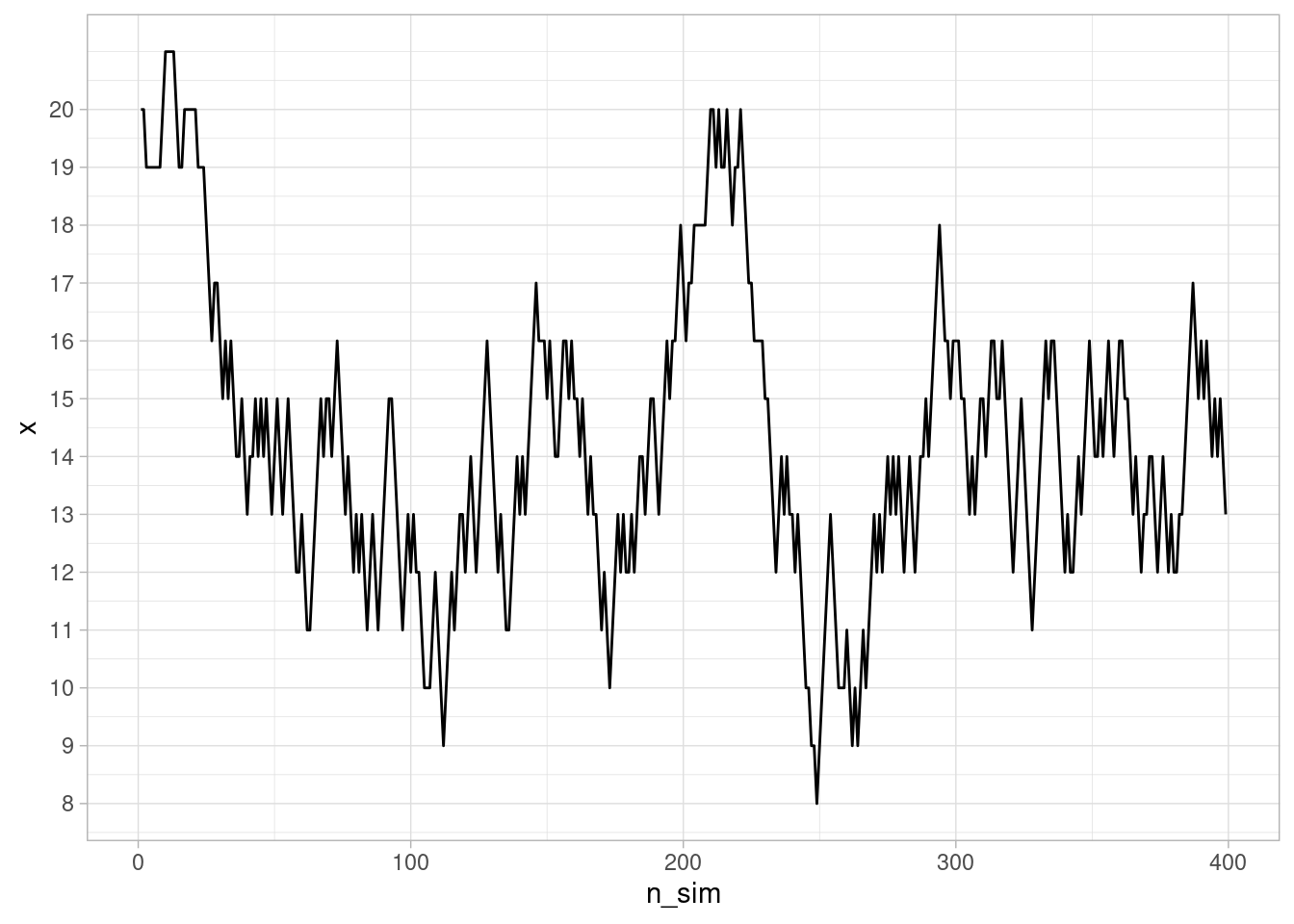

¿Cómo se comparan estos dos métodos? Podemos ver por ejemplo cómo se comparan las distribuciones aproximadas hasta cierto número de iteraciones con la verdadera distribución objetivo:

approx_sim <- map_df(seq(200, 30000, by = 200), function(n_sims){
  resumen_1 <- resultados_sim |> filter(n_sim <= n_sims) |> 
    count(x) |>
    mutate(p_aprox = n / sum(n)) |>
    select(-n) |>
    right_join(dist_obj, by = "x") |> 
    mutate(metodo = "MH-1") |> 
    mutate(n_sims = n_sims) 
  resumen_2 <- resultados_sim_2 |> filter(n_sim <= n_sims) |>
    count(x) |>
    mutate(p_aprox = n / sum(n)) |>
    select(-n) |>
    right_join(dist_obj, by = "x") |> 
    mutate(metodo = "MH-2") |> 
    mutate(n_sims = n_sims) 
  bind_rows(resumen_1, resumen_2) |> 
    mutate(p_aprox = ifelse(is.na(p_aprox), 0, p_aprox))
})

approx_sim |> 
  mutate(dif_abs = abs (p_aprox-p)) |>
  group_by(metodo, n_sims) |> 
  summarise(dif_abs = sum(dif_abs)) |> 
ggplot(aes(n_sims, dif_abs, color = metodo)) +
  geom_line() 

`summarise()` has grouped output by 'metodo'. You can override using the
`.groups` argument.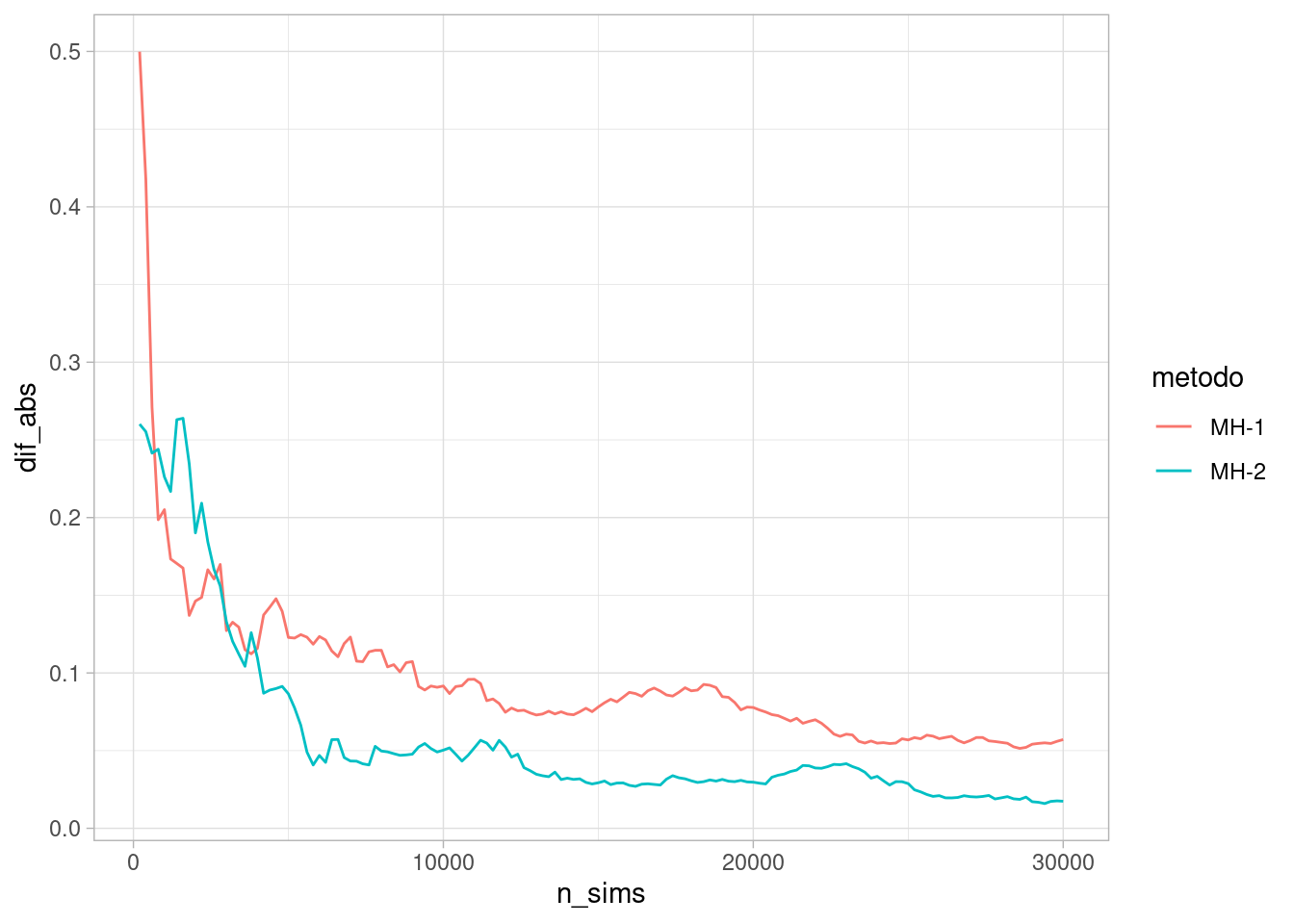

En este caso, considera qué es lo que sucede en cada uno de estos casos:

1. El algoritmo que da saltos grandes muchas veces rechaza porque cae en un área de probilidad muy baja.
2. El algoritmo que da saltos chicos puede tardar en explorar regiones de probabilidad relativamente alta con suficiente frecuencia (tarda un moverse de un lugar a otro), por su naturaleza de “caminata aleatoria”. Pero sus tasas de aceptación son más altas.

Este es el primer trade-off que existe en este algoritmo: tomar pasos grandes y balancear las probabilidades quizá rechazando muy frecuentemente (no es eficiente), o tomar pasos chicos y vagar más tiempo para visitar regiones de alta probabilidad, aunque con menos tasa de rechazo. Dependiendo de la distribución que queremos aproximar podemos inclinarnos más por una o por otra opción. En dimensiones altas generalmente ninguna combinación es muy buena.

Idea básica de MCMC

En MCMC, buscamos un cadena de Markov que, en el largo plazo, visite cada posible valor del parámetro proporcionalmente a la probabildad posterior del parámetro. En el caso multivariado es la misma idea: cada combinación de parámetros debe ser visitada por la cadena en proporción a su probabilidad posterior.

Balance detallado

¿Por qué funcionan estos algoritmos? Supongamos que en cada paso, se cumple que (balance detallado): \[{q(x|y)}p(y) = {q(y|x)}{p(x)}\] donde \(q(x|y)\) son las probabilidades de transición de nuestra cadena de Markov propuesta. Esta ecuación dice que la proporción de transiciones de \(y\) a \(x\) en relación a las transiciones de \(x\) a \(y\) es la misma que la proporción de probabilidad que hay entre \(y\) y \(x\) en la distribución objetivo.

Esta ecuación implica que si la probabilidad se distribuye como \(p(x)\), entonces al transicionar con \(q\) la probabilidad fluje de manera que se mantiene estática en \(p\), es decir \(p\) es una distribución estacionaria para la cadena de Markov producida por las transiciones.

Esto es fácil de demostrar pues \[\sum_{y} q(x|y)p(y) = \sum_{y} q(y|x)p(x) = p(x) \sum_{y} q(y|x) = p(x).\]

Bajo otros supuestos adicionales de ergodicidad (aperiodicidad y tiempos de recurrencia finitos, es decir, las transiciones mezclan bien los estados), entonces podemos simular la cadena de Markov por un tiempo suficientemente largo y con esto obtener una muestra de la distribución objetivo \(p\), es decir, la distribución estacionaria \(p(x)\) también es la distribución de largo plazo para cualquier cadena que simulemos.

¿Cómo podemos diseñar entonces las \(q(x|y)\) correspondientes?

Comenzamos considerando distribuciones propuesta \(q_0(x|y)\) que no necesariamente satisfacen la ecuación de balance, y supondremos como en los ejemplos de arriba (verifícalo) que nuestras transiciones tienen probabilidades simétricas \(q_0(y|x) = q_0(x|y)\). Entonces, cuando \(p(y)/p(x) > 1\), queremos transicionar de \(x\) a \(y\) con más frecuencia que de \(y\) a \(x\). Comenzando en \(x\), si la propuesta de \(q_0(y|x)\) es \(y\), podríamos poner entonces que el sistema transicione con probabilidad 1 a \(y\). Sin embargo, si empezamos en \(y\) y la propuesta es \(x\), ponemos que el sistema sólo transiciona de \(y\) a \(x\) con probabilidad \(p(x)/p(y)\).

De esta manera, obtenemos que bajo \(q(y|x)\), \(x\) transiciona a \(y\) con probabilidad $q_0(y|x) multiplicada por \(\min\{1, p(y)/p(x)\}\). Entonces, el cociente \(\frac{q(y|x)}{q(x|y)}\) (usando también la simetría de \(q_0(y|x)\), es igual a \(\frac{p(y)}{p(x)}\) si \(p(y)<p(x)\). Si \(p(x)>p(y)\), entonces siguiendo el mismo argumento, y por simetría de \(q_0(y|x)\), se cumple que el cociente de probabilidades es tambien igual a \(\frac{p(y)}{p(x)}\). Esto demuestra que se cumple el balance detallado.

De esta forma, balanceamos las transiciones de \(q_0(y|x)\) modificando con el proceso de adaptación y rechazo, para que la cadena de Markov resultante tenga la distribución estacionario \(p(x)\), que es la distribución objetivo.

Ejemplo: Metropolis bivariado

Supongamos ahora que quisiéramos simular de una normal multivariada con media en c(2,3) y matriz de covarianza \(\Sigma\), que supondremos es tal que la desviación estándar de cada variable es 1 y la correlación es 0.8. La matriz \(\Sigma\) tiene 1 en la diagonal y 0.8 fuera de la diagonal.

La distribución objetivo \(p\) está dada entonces (módulo una constante de proporcionalidad):

construir_log_p <- function(m, Sigma){
  Sigma_inv <- solve(Sigma)
  function(z){
    - 0.5 * (t(z-m) %*% Sigma_inv %*% (z-m))
  }
}
Sigma <- matrix(c(1, 0.8, 0.8, 1), nrow = 2)
m <- c(2, 3)
log_p <- construir_log_p(m, Sigma)

Nótese que como Metropolis hace cocientes de probabilidades, sólo es necesario conocer la densidad objetivo módulo una constante de proporcionalidad.

Una algoritmo de Metropolis podría ser el siguiente:

# simulamos
M <- 50000
metropolis_mc <- function(M, z_inicial = c(0,0), log_p, delta_x, delta_y){
  z <- matrix(nrow = M, ncol = 2)
  z[1, ] <-z_inicial
  colnames(z) <- c("x", "y")
  rechazo <- 0
  for(i in 1:(M-1)){
    x_prop <- rnorm(1, z[i, 1], delta_x)
    y_prop <- rnorm(1, z[i, 2], delta_y)
    z_prop <- c(x_prop, y_prop)
    q <- exp(log_p(z_prop) - log_p(z[i, ]))
    if(runif(1) < q){
      z[i + 1, ] <- z_prop
    } else {
      rechazo <- rechazo + 1
      z[i + 1, ] <- z[i, ]
    } 
  }
  print(rechazo / M)
  z_tbl <- as_tibble(z) |> 
    mutate(n_sim = row_number())
  z_tbl
}
z_tbl <- metropolis_mc(M, c(2.5, 3.5), log_p, 1.0, 1.0)

[1] 0.59752

Vemos que tenemos una tasa alta de rechazos. ¿Por qué? Veamos cómo se ven las simulaciones hasta 500 iteraciones:

# estas las usamos para graficar
sims_normal <- mvtnorm::rmvnorm(100000, mean = m, sigma = Sigma)
colnames(sims_normal) <- c("x", "y")
sims_normal <- as_tibble(sims_normal)
elipses_normal <-list(stat_ellipse(data = sims_normal, aes(x, y), 
               level = c(0.9), type = "norm", colour = "salmon"),
  stat_ellipse(data = sims_normal, aes(x, y), 
               level = c(0.5), type = "norm", colour = "salmon"), 
  stat_ellipse(data = sims_normal, aes(x, y), 
               level = c(0.2), type = "norm", colour = "salmon"))

graf_tbl <- map_df(seq(10, 500, 20), function(i){
  z_tbl |> filter(n_sim <= i) |> mutate(num_sims = i)
})
ggplot(graf_tbl, aes(x, y)) + 
  elipses_normal +
  geom_point(alpha = 0.1) +
  facet_wrap(~num_sims) + theme_minimal()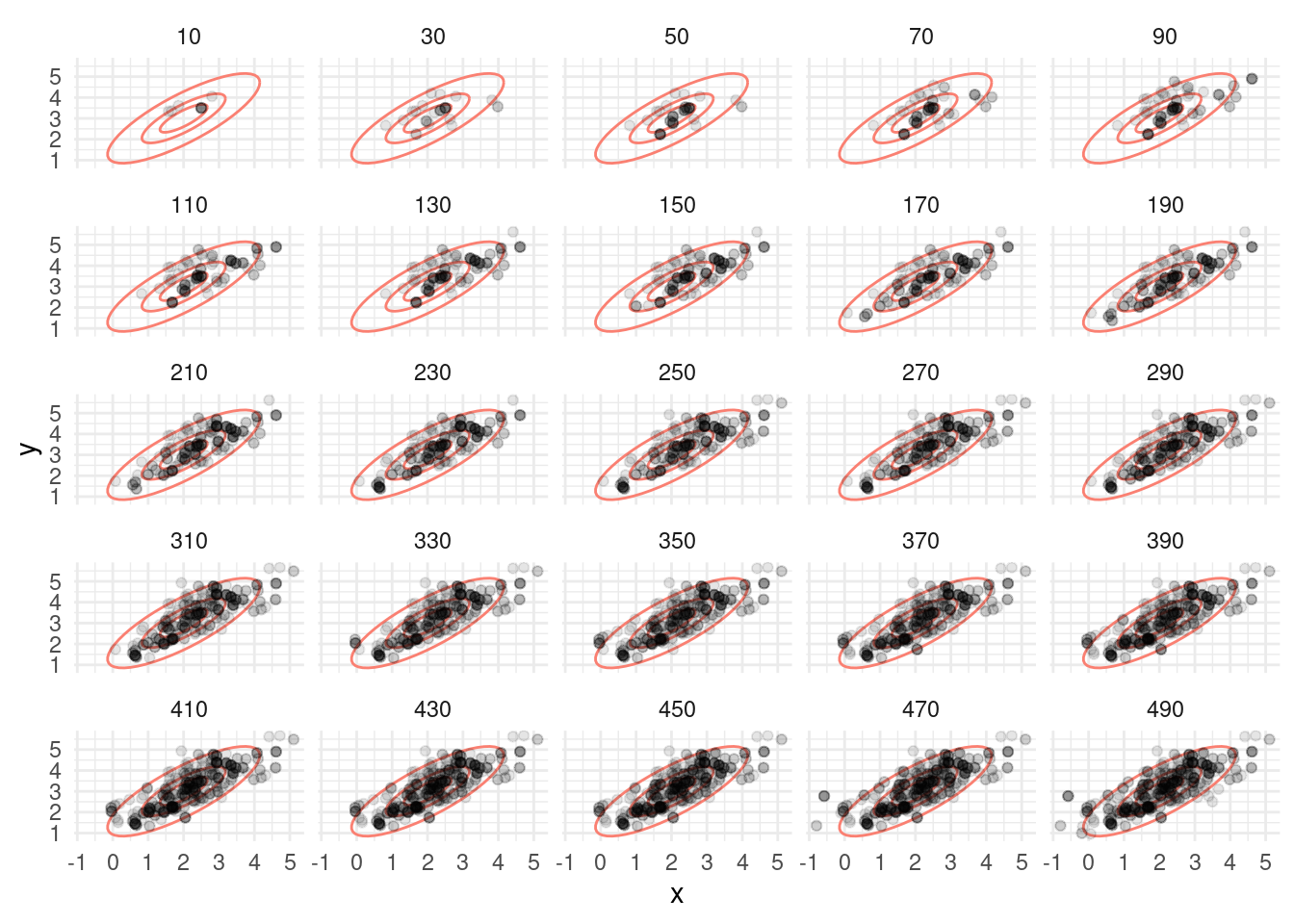

library(gganimate)
anim_mh_1 <- z_tbl |> filter(n_sim < 50) |> 
  ggplot() + 
  geom_point(aes(x, y, group = n_sim), size = 3) +
  transition_reveal(n_sim) +
  elipses_normal +
  labs(title = 'Iteración: {frame_along}') +
  theme_minimal()
anim_save(animation = anim_mh_1, filename = "figuras/mh-1-normal.gif", 
          renderer = gifski_renderer())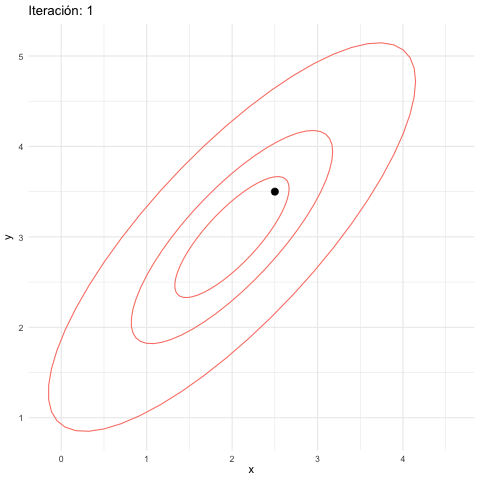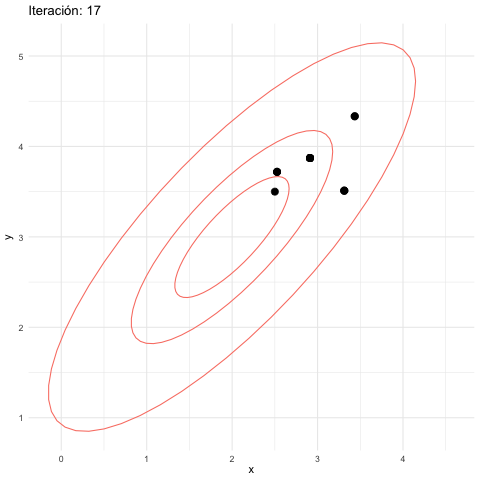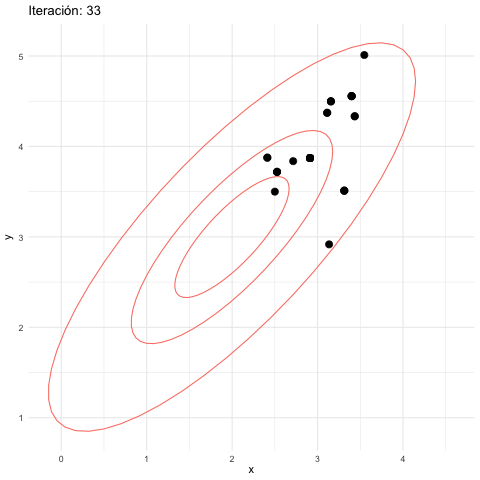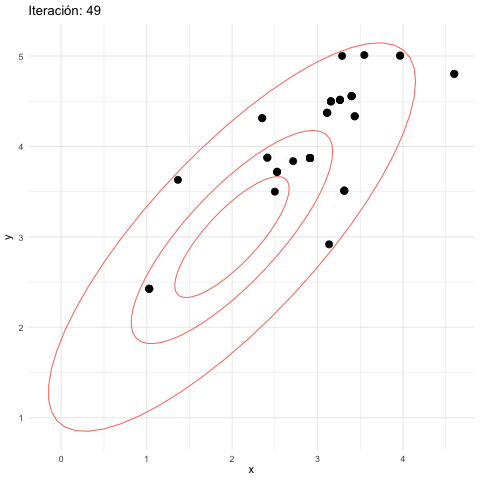

Metropolis Hastings

Observaciones:

• Los puntos que tienen intensidad alta son puntos donde hubo varios rechazos. Esto es porque las propuestas a veces caen en elipses de baja probabilidad (en la gráfica mostramos una elipse de 50% probabilidad y otra de 95%).
• Esto se debe a que los saltos en cada dirección son de desviación estándar 1, y esto fácilmente nos lleva a una zona de alta probabilidad a una de baja probabilidad.
• Sin embargo, a largo plazo, vemos cómo la cadena está visitando las regiones de alta probabilidad con aparentemente la frecuencia correcta.

Podemos entonces proponer saltos más chicos, por ejemplo:

z_tbl <- metropolis_mc(M, c(2.5, 3.5), log_p, 0.2, 0.2)

[1] 0.15584

graf_tbl <- map_df(seq(10, 500, 20), function(i){
  z_tbl |> filter(n_sim <= i) |> mutate(num_sims = i)
})
ggplot(graf_tbl, aes(x, y)) + 
  stat_ellipse(data = sims_normal, aes(x, y), 
               level = c( 0.9), type = "norm", colour = "salmon") +
  stat_ellipse(data = sims_normal, aes(x, y), 
               level = c( 0.5), type = "norm", colour = "salmon") +
  geom_point(alpha = 0.1) +
  facet_wrap(~num_sims) + theme_minimal()

anim_mh_2 <- z_tbl |> filter(n_sim < 150) |> 
  ggplot() + 
  geom_point(aes(x, y, group = n_sim), size = 3) +
  transition_reveal(n_sim) +
  elipses_normal +
  labs(title = 'Iteración: {frame_along}') +
  theme_minimal()
anim_save(animation = anim_mh_2, filename = "figuras/mh-2-normal.gif", 
          renderer = gifski_renderer())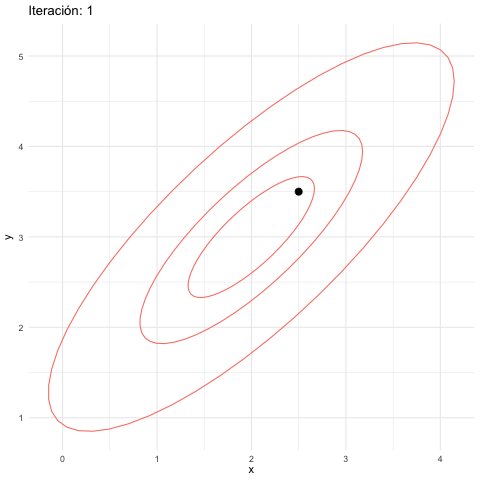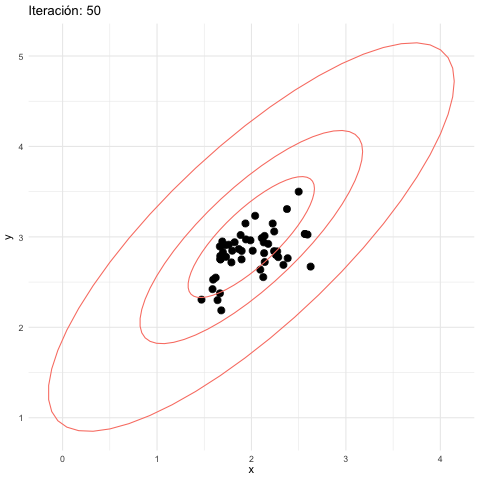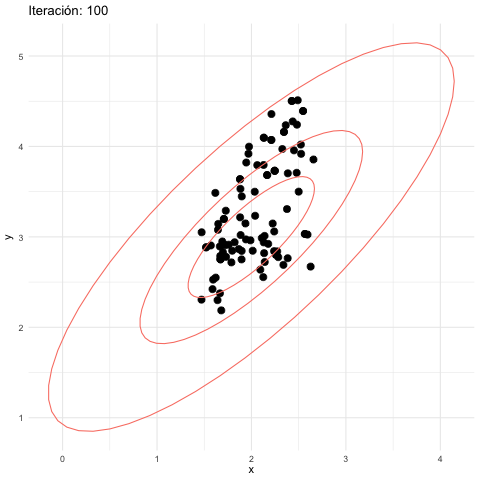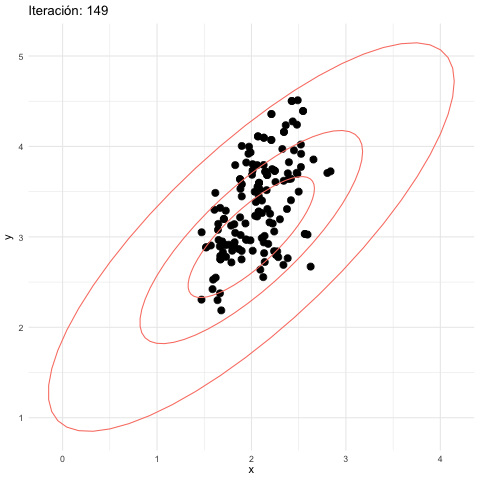

Metropolis Hastings salto chico

Observaciones:

• En este caso tenemos una tasa de aceptación más alta.
• Sin embargo, la cadena parece “vagar” en la regiones de probabilidad alta, y tiene dificultades para explorar correctamente estas regiones: se comporta localmente como una caminata aleatoria.
• Sin embargo, a largo plazo, vemos cómo la cadena está visitando las regiones de alta probabilidad con aparentemente la frecuencia correcta.

Metropolis-Hastings

En el algoritmo de Metropolis Hastings hay una tensión natural entre el tamaño de salto y la tasa de aceptación. Si el tamaño de los saltos es muy grande, la tasa de aceptación puede ser baja y esto producen ineficiencias. Si el tamaño de los saltos es muy chico, la tasa de aceptación es más alta, pero esto también es ineficiente pues la cadena puede explorar muy lentamente el espacio de parámetros.

Existen métodos que pueden superar este problema, como son muestreo de Gibbs y Monte Carlo Hamiltoniano. El primero no lo discutiremos, pues requiere poder simular fácilmente de cada parámetro dados los otros, y esto no siempre es posible. Veremos más el segundo, donde usaremos información del gradiente de la distribución objetivo para proponer exploración más eficiente.

8.2 Monte Carlo Hamiltoniano

Una manera de mejorar la exploración de Metropolis es utilizar una distribución de propuestas más apropiada. La intuición en el caso anterior es:

• Hay direcciones de más curvatura de la posterior que otras: movimientos relativamente chicos en las direcciones de alta curvatura nos llevan a regiones de probabilidad demasiado baja, y entonces tendemos a rechazar. Pero hacer movimientos aún más chicos para evitar rechazos nos lleva a explorar muy lentamente el espacio de parámetros.
• Podríamos evitar esto si nuestros saltos siguieran la curvatura natural de la distribución, como una pelota que rueda por la superficie de la distribución objetivo (con signo negativo, de forma que regiones de probabilidad alta sean valles o regiones bajas).

La idea de HMC es considerar el problema de muestrear de una distribución como un problema físico, donde introducimos aleatoridad solamente en cuanto a la “energía” de la pelota que va a explorar la posterior. Inicialmente impartimos un momento tomado al azar a la pelota, seguimos su trayectoria por un tiempo y el lugar a donde llega es nuestra nueva simulación. Esto permite que podamos dar saltos más grandes, sin “despeñarnos” en regiones de probabilidad muy baja y así evitar rechazos.

Adicionalmente, veremos que si definimos el sistema físico apropiadamente, es posible obtener ecuaciones de balance detallado, lo cual en teoría nos garantiza una manera de transicionar que resultará a largo plazo en una muestra de la distribución objetivo.

Formulación Hamiltoniana 1: introducción

Primero veremos cuál es la formulación Hamiltoniana (muy simple) de un sistema físico que nos sirve para encontrar la trayectoria de partículas del sistema. Consideremos una sola partícula cuya posición está dada por \(q\), que suponemos en una sola dimensión. La partícula rueda en una superficie cuya altura describimos como \(V(q)\), y tiene en cada instante tiene momento \(p = m\dot{q}\).

El Hamiltoniano es la energía total de este sistema, en el espacio fase que describe el estado de cada partícula dadas su posición y momento \((p,q)\), y es la suma de energía cinética más energía potencial:

\(H(p,q) = T(p) + V(q)\)

donde \(V(q) = q^2/2\) está dada y \(T(p) = \frac{p^2}{2m}\), de modo que

\[H(p, q) = \frac{p^2}{2m} + V(q) = \frac{p^2}{2m} + \frac{q^2}{2}\]

Ahora consideremos las curvas de nivel de \(H\) (energía total constante), que en este caso se conservan a lo largo del movimiento de la partícula. Como sabemos por cálculo, estas curvas son perpendiculares al gradiente del Hamiltoniano, que es \((\partial{H}/\partial{p}, \partial{H}/\partial{q})\). El movimiento de las partículas, sin embargo, es a lo largo de las curvas de nivel, de manera que el flujo instantáneo debe estar dado por el gradiente de \(H\) rotado 90 grados, es decir, por \((\partial{H}/\partial{q}, -\partial{H}/\partial{p})\).

Entonces tenemos que el movimiento de la partícula debe cumplir las ecuaciones de Hamilton:

\[\frac{dp}{dt} = \frac{\partial{H}}{\partial{q}}, \frac{dq}{dt} = -\frac{\partial{H}}{\partial{p}}\] Simplificando y usando la definición de \(H\), obtenemos que \[\frac{dq}{dt} = \frac{p}{m}, \frac{dp}{dt} = -\frac{\partial{V}}{\partial{q}} = -q\] Ilustramos este campo vectorial en la siguiente gráfica, donde escogemos \(V(q) = q^2/2\), \(m=1\), y dibujamos algunas curvas de nivel del Hamiltoniano:

espacio_fase_1 <- tibble(p = seq(-3, 3, length.out = 1000), q = seq(-3, 3, length.out = 1000)) |> 
  expand(p, q) |> 
  mutate(dq = p, dp = -q) |> 
  mutate(H = p^2/2 + q^2/2)
espacio_fase <- tibble(p = seq(-3, 3, length.out = 10), q = seq(-3, 3, length.out = 10)) |> 
  expand(p, q) |> 
  mutate(dq = p, dp = -q)
espacio_fase |> 
  ggplot(aes(p, q)) +
  geom_contour(data = espacio_fase_1, aes(x = p, y = q, z = H)) +
  geom_segment(aes(xend = p + dp/5, yend = q + dq/5), 
               arrow = arrow(length = unit(0.1, "inches"))) +
  theme_minimal() +
  labs(subtitle = "Movimiento en espacio fase: 1 dimensión")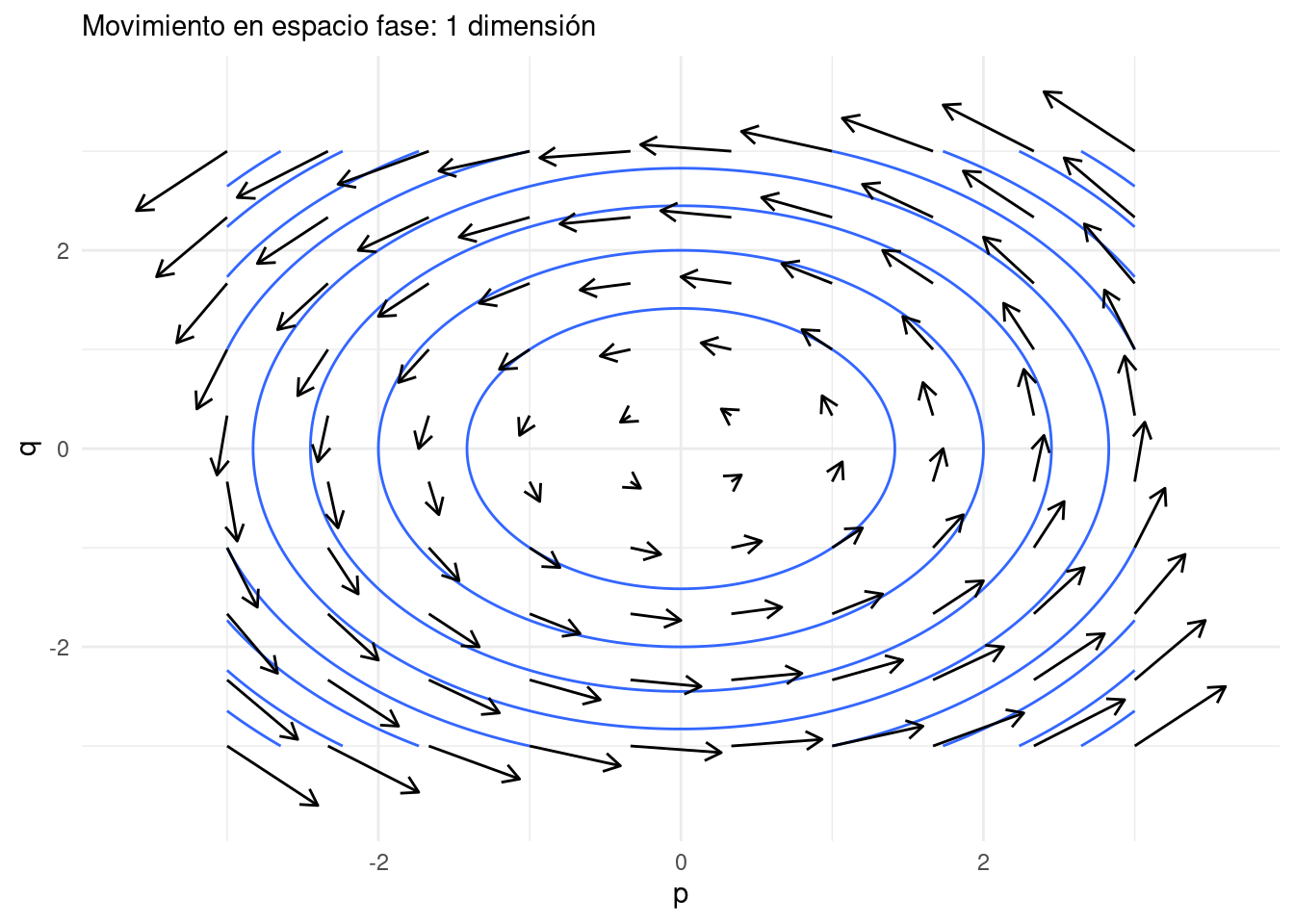

Ojo: este no es le movimiento de una partícula en dimensión 2: es el movimiento de la partícula en el espacio fase \((p,q)\), y la variable de posición \(q\) es de dimensión 1. Los ciclos de la gráfica muestran como conforme la partícula se mueve, energía potencial y cinética se intercambian a lo largo de su trayectoria en un “hilo”.

Formulación Hamiltoniana 2: densidades de probabilidad

Consideremos una partícula en el espacio de parámetros \(\theta\). En esta formulación, si \(\theta\) son los parámetros de interés, consideramos la energía potencial del sistema como \(V(p) = -\log p(\theta)\), donde \(p(\theta)\) es la distribución objetivo.

Buscamos simular del sistema con ecuaciones de movimiento para \(\theta\). Como hicimos antes, vamos a “levantar” al espacio fase incluyendo el momento, que denotaremos como \(\rho\). La energía cinética, en el caso más simple, podemos definirla (en la práctica existen reescalamientos) como como \(T(\rho) =\frac{1}{2}\sum_i \rho_i^2\) (la energía cinética es proporcional al momento cuadrado, pues el momento es masa por velocidad).

El Hamiltoniano por definición \(H(\rho, \theta) = T(\rho) + V(\theta)\), y las ecuaciones de Hamilton son las mismas que arriba, que en este caso nos dan

\[\frac{d\theta}{dt} = \rho, \frac{d\rho}{dt} = \nabla(\log(p(\theta)).\]

Si resolvemos estas ecuaciones, podemos entonces simular del sistema como sigue:

1. Dado un punto inicial \(\theta\), escogemos un momento inicial \(\rho\) al azar, por ejemplo cada componente normal \(N(0,1)\) (en la práctica existe un reescalamiento, pero en general queremos que \(p(\rho) = p(-\rho)\)). Es decir, agregamos inicialmente una cantidad aleatoria de energía a la partícula.
2. Usando las ecuaciones de Hamilton, actualizamos la posición \(\theta\) y el momento de la partícula un cierto tiempo \(t\) fijo, de manera que no quedemos muy cerca del valor inicial, pero tampoco hagamos demasiado trabajo computacional.
3. La posición nueva \(\theta^*\) es aceptada como nuestra nueva simulación (si el paso 2 es exacto, pero frecuentemente no lo es).
4. Repetimos los pasos 1-3 un número suficiente de veces para obtener simulaciones de la posterior.

Este método produce simulaciones de la distribución objetivo bajo condiciones de regularidad. Podemos demostrar por ejemplo, que se cumple el balance detallado.

Balance detallado para HMC

Supongamos que las transiciones que da este sistema son \(q(y|x)\). Nótese que dado el momento simulado, tenemos el estado \((\rho, x)\), y la transición \(x\to\y\) es determinista, gobernada por las ecuaciones de Hamilton. Escribimos la transición como \[(\rho, x) \to (\rho^*, y).\] Nótese que \(\rho\) y \(x\) determinan la transición, de modo que

\[p(x)q(y|x) = p(x)p(\rho) = \exp(-H(\rho, x)) = \exp(-H(\rho^*, y))\] Que es cierto por conservación de la energía total y la transición sigue exactamente trayectorias del Hamiltoniano. Esta última cantidad, usando un argumento similar, es igual a

\[p(y)p(\rho^*) = p(y)p(-\rho^*) = p(y) q(x|y)\] La segunda igualdad se da porque \(p(\rho)\) es Gaussiana (simétrica). Y finalmente, la última igualdad se da porque si necesitamos momento \(\rho\) para llegar de \(x\) a \((\rho^*, y)\), entonces necesitamos \(-\rho^*\) (volteamos la velocidad ifnal) para llegar de \(y\) a \((\rho, x)\), pues el sistema físico es reversible.

Nótese que este argumento se rompe si por ejemplo si es imposible transicionar de un punto a otro (por ejemplo, cuando la distribución objetivo \(p\) tiene dos regiones separadas de probabilidad positiva).

Integración de las ecuaciones de Hamilton

Para aproximar soluciones de estas ecuaciones diferenciales utilizamos el integrador leapfrog, en el que hacemos actualizaciones alternadas de posición y momento con un tamaño de paso \(\epsilon\) chico. Hacemos este paso un número \(L\) de veces, para no quedar muy cerca del valor inicial.

En nuestro ejemplo, actualizaríamos por ejemplo el momento a la mitad del paso:

\[\rho_{t+\epsilon/2} = \rho_t - \frac{\epsilon}{2}\nabla(\log(p(\theta_t)))\] Seguido de una actualización de la posición:

\[\theta_{t+\epsilon} = \theta_t + \epsilon \rho_{t+\epsilon/2}\] y finalmente otra actualización del momento:

\[\rho_{t+\epsilon} = \rho_{t+\epsilon/2} - \frac{\epsilon}{2}\nabla(\log(p(\theta_{t+\epsilon})))\] Al final de este proceso, encontraremos que por errores numéricos, quizá el Hamiltoniano varió un poco. Si esto sucede, podemos hacer un paso de aceptación y rechazo como en Metropolis Hastings, donde la probabilidad de aceptar es

\[\min\left(1, \exp(H(\rho,\theta) - H(\rho^{*},\theta^{*}))\right)\] donde \(\rho^{*}\) y \(\theta^{*}\) son los valores de momento y posición nuevos y \(H(\rho,\theta)\) es el Hamiltoniano en el paso anterior.

Observaciones:

1. Un caso posible obtengamos desbordes o casi desbordes numéricos del momento o la posición (el Hamiltoniano en el punto inicial es órdenes de magnitud diferente que el inicial, ver el manual de Stan ). Esto indica problemas graves con el algoritmo de integración, y en general marcamos estas iteraciones como divergentes. Estas fallas pueden producir, como veremos, exploración insuficiente de la distribución objetivo.
2. Si queremos usar HMC directamente, es delicado afinar el tamaño de paso, la distribución de propuesta para el momento, y el número de saltos \(L\). En Stan, que usa una variación de HMC, estos valores son ajustados en el periodo de calentamiento o warmup, antes de

Ejemplo: HMC en una distribución normal bivariada

Primero calculamos el gradiente que requerimos. En este caso, podemos hacerlo analíticamente:

construir_log_p <- function(m, Sigma){
  Sigma_inv <- solve(Sigma)
  function(z){
    - 0.5 * (t(z-m) %*% Sigma_inv %*% (z-m))
  }
}
Sigma <- matrix(c(1, 0.8, 0.8, 1), nrow = 2)
m <- c(2, 3)
log_p <- construir_log_p(m, Sigma)
# en diferenciación automática, el siguiente constructor
# puede tomar como argumento log_p, pero aquí la escribimos
# explícitamente
construir_grad_log_p <- function(m, Sigma){
  Sigma_inv <- solve(Sigma)
  function(theta){
    - Sigma_inv %*% (theta-m)
  }
}
grad_log_p <- construir_grad_log_p(m, Sigma)
construir_H <- function(m, Sigma){
  Sigma_inv <- solve(Sigma)
  function(theta, rho){
    - log_p(theta) + 0.5 * sum(rho^2)
  }
}
H <- construir_H(m, Sigma)
log_p(c(1,3))

          [,1]
[1,] -1.388889

grad_log_p(c(1,3))

          [,1]
[1,]  2.777778
[2,] -2.222222

Ahora, implementamos el algoritmo de HMC. Primero, definimos una función

hamilton_mc <- function(n, theta_0 = c(0,0), log_p, grad_log_p, epsilon, L){
  p <- length(theta_0)
  theta <- matrix(0, n, p)
  theta[1, ] <- theta_0
  rho <- matrix(0, n, p)
  theta_completa <- matrix(0, n*L, p)
  theta_completa[1, 0] <- theta_0
  rho_completa <- matrix(0, n*L, p) 
  indice_completa <- 2
  rechazo <- 0
  for(i in 2:n){
    prop_rho <- rnorm(p)
    rho[i-1, ] <- prop_rho
    prop_theta <- theta[i-1, ]
    for(t in 1:L){
      prop_rho <- prop_rho + 0.5 * epsilon * grad_log_p(prop_theta)
      prop_theta <- prop_theta + epsilon * prop_rho 
      prop_rho  <- prop_rho + 0.5 * epsilon * grad_log_p(prop_theta)
      theta_completa[indice_completa,] <- prop_theta
      rho_completa[indice_completa,] <- prop_rho
      indice_completa <- indice_completa + 1
    }
  
    q <- min(1, exp(H(theta[i-1, ], rho[i-1, ]) - 
                  H(prop_theta, prop_rho))) 
    if(runif(1) < q){
      theta[i, ] <- prop_theta
    } else {
      rechazo <- rechazo + 1
      theta[i, ] <- theta[i-1, ]
      rho[i, ] <- rho[i-1, ]
      theta_completa[indice_completa - 1,] <- theta[i-1, ]
      rho_completa[indice_completa - 1,] <- rho[i-1, ]
    } 
  }
  print(rechazo / n)
  list(sims = tibble(x = theta[,1], y = theta[,2]),
       trayectorias = tibble(x = theta_completa[,1], y = theta_completa[,2]) |>
         mutate(iteracion = rep(1:n, each = L), paso = rep(1:L, times = n)))
}

Revisamos que la muestra aproxima apropiadamente nuestra distribución

set.seed(10)
hmc_salida <- hamilton_mc(1000, c(0,0), log_p, grad_log_p, 0.2, 12)

[1] 0.016

ggplot(hmc_salida$sims, aes(x = x, y = y)) + geom_point() +
  stat_ellipse(data = sims_normal, aes(x, y), 
               level = c(0.9), type = "norm", colour = "salmon") +
  stat_ellipse(data = sims_normal, aes(x, y), 
               level = c( 0.5), type = "norm", colour = "salmon") +
  stat_ellipse(level = c( 0.9), colour = "green", type = "norm") +
  stat_ellipse(level = c( 0.5), colour = "green", type = "norm")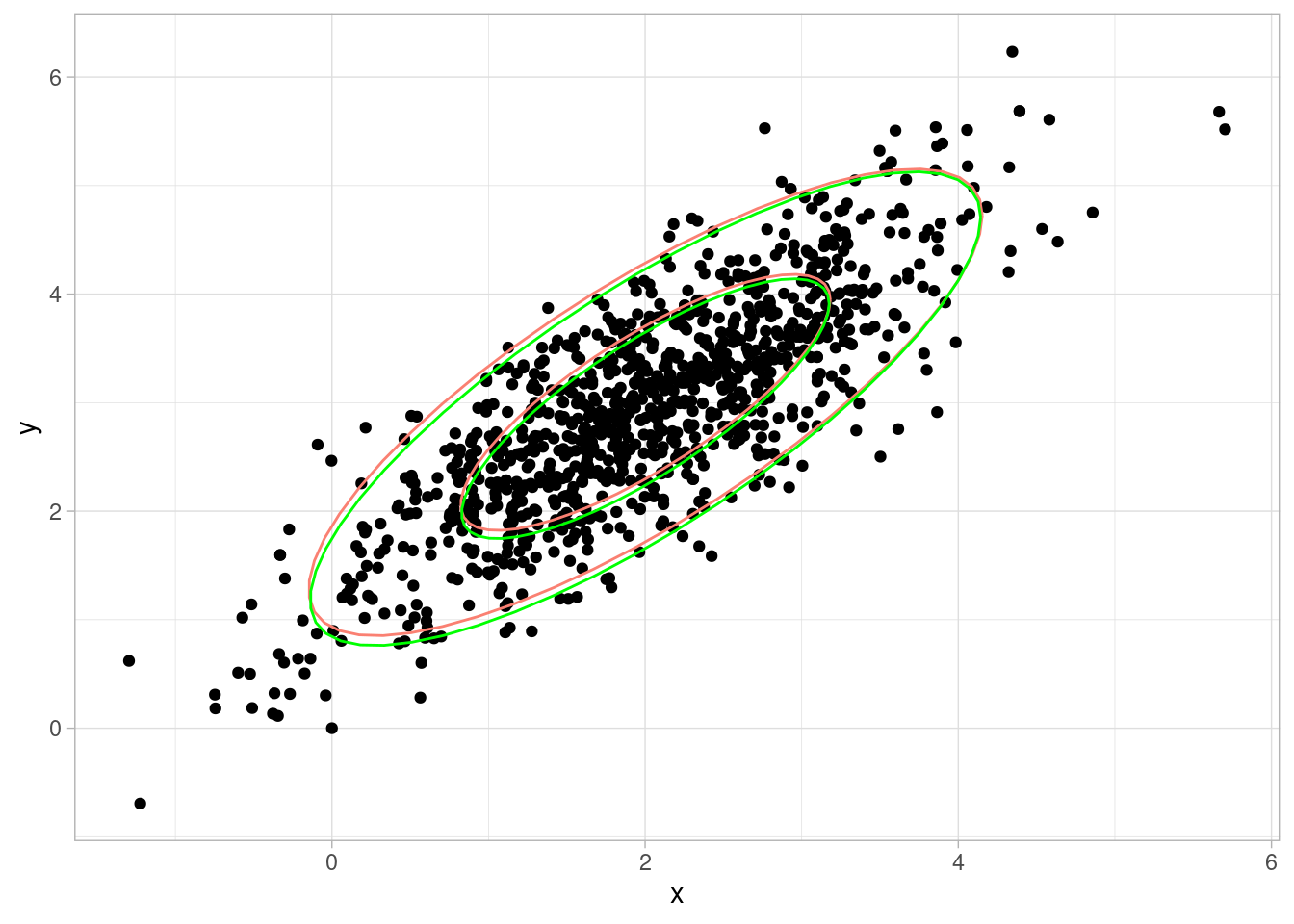 

tray_tbl <- hmc_salida$trayectorias
head(tray_tbl)

# A tibble: 6 × 4
        x      y iteracion  paso
    <dbl>  <dbl>     <int> <int>
1  0      0              1     1
2 -0.0185 0.0409         1     2
3 -0.0757 0.231          1     3
4 -0.148  0.545          1     4
5 -0.201  0.940          1     5
6 -0.192  1.37           1     6

library(gganimate)
anim_hmc <- ggplot(tray_tbl |> mutate(iter = 4*as.numeric(paso == 1), 
                          s = as.numeric(paso == 2)) |> 
         filter(iteracion < 30) |> 
         mutate(tiempo = row_number()) |> 
         mutate(tiempo = tiempo + cumsum(50 * s)), 
       aes(x = x, y = y)) + 
    geom_point(aes(colour = iter, alpha = iter, size = iter, group = tiempo)) +
    geom_path(colour = "gray", alpha = 0.5) +
  transition_reveal(tiempo) +
  elipses_normal +
  theme(legend.position = "none") 
anim_save(animation = anim_hmc, filename = "figuras/hmc-normal.gif", 
          renderer = gifski_renderer())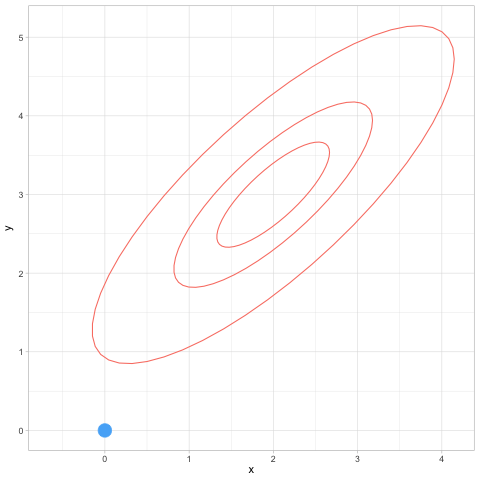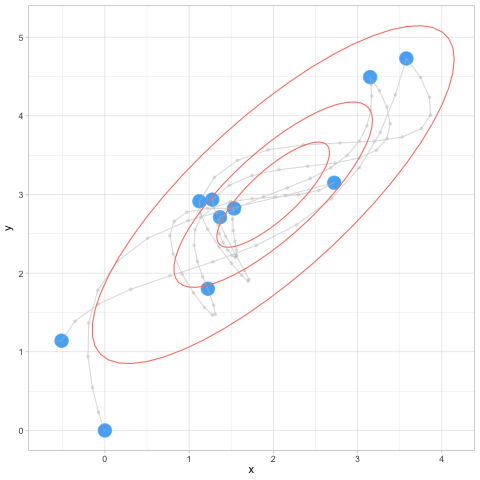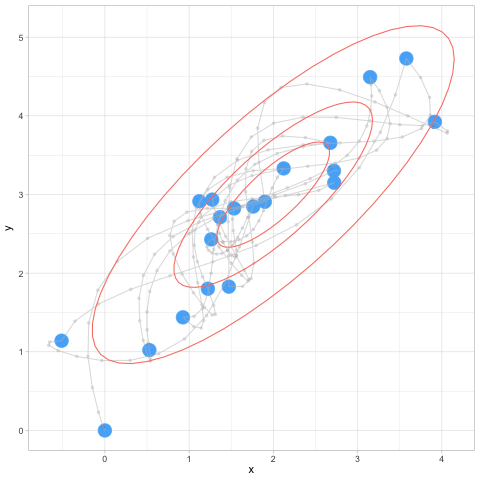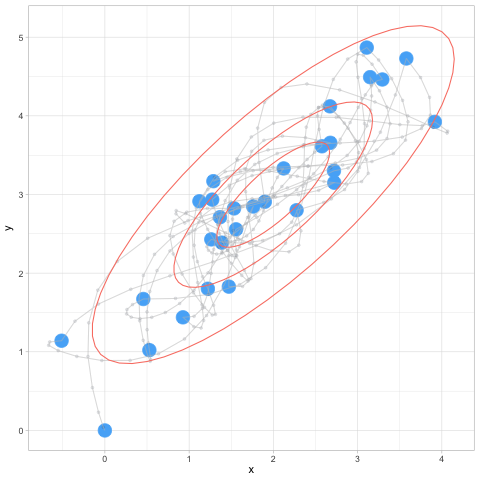

HMC

Observaciones:

• Nótese que ahora podemos dar pasos más grandes a lo largo de los lugares donde concentra mayor probabilidad.
• Esto implica dos cosas: evitamos el comportamiento de caminata aleatoria (pasos muy cortos), y también tasas de rechazo alto (cuando los pasos son muy grandes en HMC)
• El algoritmo utiliza información adicional: además de calcular la posterior, como en metropolis, es necesario calcular también el gradiente de la posterior.
• Este algoritmo hace más trabajo para cada iteración (requiere la integración leapfrog), pero cada iteración es más informativa
• Bien afinado, funciona para problemas de dimensión alta (cientos o miles de parámetros), donde geométricamente la densidad está concentrada en un espacio geométricamente chico. Existen todavía dificultades que discutiremos en otros modelos más adelante.

Tip

Observamos que hasta ahora no hemos aplicado estos algoritmos para simular de la posterior de un modelo: hemos tomado distribuciones fijas y usamos MCMC para simular de ellas. El proceso para una posterior es el mismo, pero usualmente más complicado pues generalmente involucra mucho más parámetros y una posterior que no tiene una forma analítica conocida.

Sin embargo, la aplicación para una posterior es la misma: siempre podemos calcular el logaritmo de la posterior (al menos hasta una constante de proporcionalidad), y siempre podemos usar diferenciación automática para calcular el gradiente de la log posterior. Podemos aplicar entonces HMC o Metropolis.

Comparación de HMC y Metropolis

Finalmente, haremos una comparación entre el desempeño de HMC y Metropolis en el caso de la distribución normal. Utilizaremos otra normal bivariada con más correlación.

set.seed(737)
Sigma <- matrix(c(1, -0.9, -0.9, 1), nrow = 2)
m <- c(1, 1)
log_p <- construir_log_p(m, Sigma)
grad_log_p <- construir_grad_log_p(m, Sigma)
system.time(hmc_1 <- hamilton_mc(1000, c(1,2), log_p, grad_log_p, 0.2, 12))

[1] 0.042

   user  system elapsed 
  0.065   0.000   0.065 

system.time(metropolis_1 <- metropolis_mc(1000, c(1,2), log_p, 0.2, 0.2))

[1] 0.204

   user  system elapsed 
  0.018   0.000   0.017 

system.time(metropolis_2 <- metropolis_mc(1000, c(1,2), log_p, 1, 1))

[1] 0.692

   user  system elapsed 
  0.018   0.000   0.018 

sims_hmc <- hmc_1$sims |> mutate(n_sim = row_number()) |> 
  mutate(algoritmo = "hmc")
sims_metropolis_1 <- metropolis_1 |> 
  mutate(algoritmo = "metropolis (corto)") 
sims_metropolis_2 <- metropolis_2 |> 
  mutate(algoritmo = "metropolis (largo)") 
sims_comp <- bind_rows(sims_hmc, sims_metropolis_1, sims_metropolis_2)
anim_comp <- ggplot(sims_comp |> filter(n_sim < 200)) + 
  transition_reveal(n_sim) +
  theme(legend.position = "none") +
  geom_path(aes(x, y), colour = "gray", alpha = 0.2) + 
    geom_point(aes(x, y, group = n_sim)) +
  facet_wrap(~algoritmo)
anim_save(animation = anim_comp, filename = "figuras/comparacion-normal.gif", height = 250, width = 500,
          units = "px",
          renderer = gifski_renderer())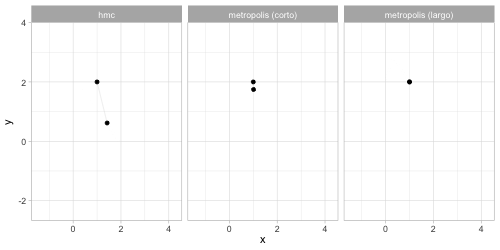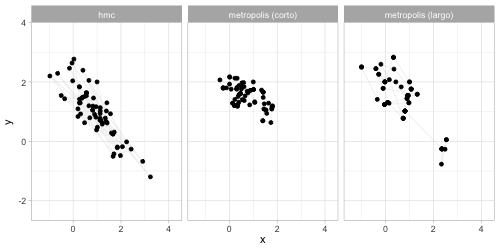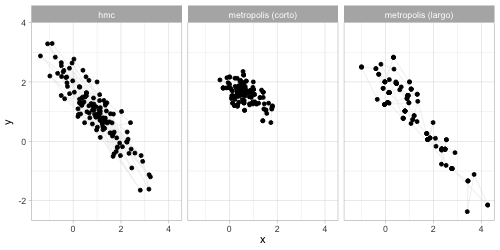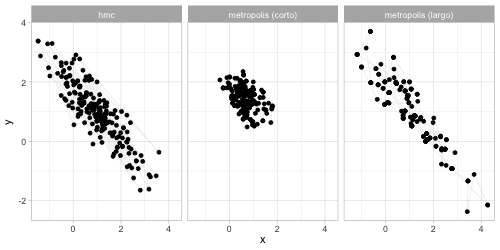

Comparación

HMC en Stan

En Stan se incluyen tres componentes adicionales importantes para estimar posteriores de manera eficiente:

1. Periodos de warm-up (calentamiento) y sampling (muestreo). En el periodo de calentamiento, el muestreador afina tamaños de paso, escalamiento de la distribución de propuesta (normal multivariada), y otros parámetros de manera automática.
2. Implementación de diferenciación automática para no tener que calcular el grandiente de la log posterior directamente. A partir del código que damos, se crean automáticamente funciones que calculan el grandiente (no es una aproximación numérica).
3. Implementación de HMC sin vueltas en U (NUTS): una afinación adicional es dinámicamente adaptar el número de pasos de integración para evitar “regresos”, como vimos que sucedía en los ejemplos de arriba. Ver por ejemplo aquí, o la documentación de Stan.

8.3 Diagnósticos de convergencia

Aunque casi nunca es posible demostrar rigurosamente que las simulaciones de un algoritmo MCMC dan buena aproximación de la distribución posterior de interés, especialmente con HMC y NUTS, tenemos muchos diagnósticos que fallan cuando existen problemas serios.

En primer lugar, será útil correr distintas cadenas con valores iniciales aleatorios diferentes, analizamos cada una y las comparamos entre sí. Recordamos que cada una de estas cadenas tiene como distribución estacionaria límite la distribución posterior. Diagnósticos que indican que las cadenas se comportan de manera muy distinta, explorando distintas regiones del espacio de parámetros, o que no han convergido porque exploran lentamente el espacio de parámetros, son señales de problemas.

Los diagnósticos más comunes son:

1. Traza de cadenas
2. Medida R-hat de convergencia: mide la variabilidad entre cadenas y dentro de cadenas.
3. Número de muestras efectivas (ESS) y autocorrelación.
4. Transiciones divergentes.

Modelos con variables latentes

Veremos el ejemplo de calificación de vinos de distintos países de McElreath (2020), sus diagnósticos, y aprovecharemos para introducir variables no observadas o latentes para enriquecer nuestras herramientas de modelación.

Nuestra pregunta general es si el país de origen de los vinos influye en su calidad. Los datos que tenemos son calificaciones de vinos de distintos países por distintos jueces. La calidad del vino no la observamos directamente, sino que es causa de las calificaciones que recibe. Para construir nuestro diagrama, las consideraciones básicas son:

1. El origen del vino es una causa del calidad del vino (es nuestra cantidad a estimar).
2. Los jueces tienen distintas maneras de calificar, de manera que son causa de variación en las calificaciones (hay jueces más duros, otros más barcos, etc.) No observamos directamente que tan “duro” es cada juez.
3. Los jueces califican vinos de distintos países de manera ciega. Sin embargo es posible que reconozcan el país de origen por las características de los vinos, de manera que puede existir un efecto directo de Origen en Calificación (no pasa por Calidad).
4. Es posible que Jueces de distintos países tienen distintos estándares de calificación.

library(DiagrammeR)
grViz("
digraph {
  graph [ranksep = 0.2, rankdir = LR]
  node [shape=plaintext]
    Origen
    Score
    Origen_Juez
  node [shape = circle]
    Q
    J
  edge [minlen = 3]
    Origen -> Q
    Origen -> Score
    Q -> Score
    J -> Score
    Origen_Juez -> J
}
")

Y vemos, por nuestro análisis del DAG, que podemos identificar el efecto de Origen sobre Calidad sin necesidad de estratificar por ninguna variable (no hay puertas traseras). Sin embaergo, podemos estratificar por Juez para obtener más precisión (ver sección anterior de buenos y malos controles).

8.3.0.1 Primera iteración: modelo simple

Comenzamos con un modelo simple, y lo iremos construyendo para obtener la mejor estimación posible de la influencia del país de origen en la calidad del vino. Nuestro primer modelo consideramos que la calificación de cada vino depende de su calidad, y modelamos con una normal:

\[S_i \sim \text{Normal}(\mu_i, \sigma)\] donde \[\mu_i = Q_{vino(i)}\]. Nuestra medida de calidad tiene escala arbitaria. Como usaremos la calificación estandarizada, podemos poner \[Q_j \sim \text{Normal}(0, 1).\] finalmente, ponemos una inicial para \(\sigma\), por ejemplo \(\sigma \sim \text{Exponential}(1)\) (puedes experimentar con una normal truncada también)

library(cmdstanr)

This is cmdstanr version 0.7.1

- CmdStanR documentation and vignettes: mc-stan.org/cmdstanr

- CmdStan path: /home/runner/.cmdstan/cmdstan-2.34.0

- CmdStan version: 2.34.0

A newer version of CmdStan is available. See ?install_cmdstan() to install it.
To disable this check set option or environment variable CMDSTANR_NO_VER_CHECK=TRUE.

mod_vinos_1 <- cmdstan_model("./src/vinos-1.stan")
print(mod_vinos_1)

data {
  int<lower=0> N; //número de calificaciones
  int<lower=0> n_vinos; //número de vinos
  int<lower=0> n_jueces; //número de jueces
  vector[N]  S;
  array[N]  int juez;
  array[N]  int vino;
}

parameters {
  vector[n_vinos] Q;
  real <lower=0> sigma;
}

transformed parameters {
  vector[N] media_score;
  // determinístico dado parámetros
  for (i in 1:N){
    media_score[i] = Q[vino[i]];
  }
}

model {
  // partes no determinísticas
  S ~ normal(media_score, sigma);
  Q ~ std_normal();
  sigma ~ exponential(1);
}

# Wines 2022 de Statistical Rethinking
wines_2012 <- read_csv("../datos/wines_2012.csv")

Rows: 180 Columns: 6
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (3): judge, flight, wine
dbl (3): score, wine.amer, judge.amer

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

glimpse(wines_2012)

Rows: 180
Columns: 6
$ judge      <chr> "Jean-M Cardebat", "Jean-M Cardebat", "Jean-M Cardebat", "J…
$ flight     <chr> "white", "white", "white", "white", "white", "white", "whit…
$ wine       <chr> "A1", "B1", "C1", "D1", "E1", "F1", "G1", "H1", "I1", "J1",…
$ score      <dbl> 10.0, 13.0, 14.0, 15.0, 8.0, 13.0, 15.0, 11.0, 9.0, 12.0, 1…
$ wine.amer  <dbl> 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0,…
$ judge.amer <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…

wines_2012 <- wines_2012 |> 
  mutate(juez_num = as.numeric(factor(judge)),
         vino_num = as.numeric(factor(wine))) |> 
  mutate(score_est = (score - mean(score))/sd(score))

n_jueces <- length(unique(wines_2012$juez_num))
n_vinos <- length(unique(wines_2012$vino_num))
c("num_vinos" = n_jueces, "num_jueces" = n_vinos, "num_datos" = nrow(wines_2012))

 num_vinos num_jueces  num_datos 
         9         20        180 

datos_lst <- list(
  N = nrow(wines_2012),
  n_vinos = n_vinos,
  n_jueces = n_jueces,
  S = wines_2012$score_est,
  vino = wines_2012$vino_num,
  juez = wines_2012$juez_num
)
ajuste_vinos_1 <- mod_vinos_1$sample(
  data = datos_lst,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 1000,
  iter_sampling = 2000,
  refresh = 1000,
  step_size = 0.1,
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 1 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 1 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 1 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 2 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 2 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 2 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 2 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 3 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 3 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 3 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 3 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 4 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 4 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 4 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 1 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 2 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 3 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 1 finished in 0.3 seconds.
Chain 2 finished in 0.4 seconds.
Chain 3 finished in 0.4 seconds.
Chain 4 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 finished in 0.4 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.4 seconds.
Total execution time: 0.7 seconds.

Vemos que hay variabilidad en los vinos:

ajuste_vinos_1$summary(c("Q", "sigma")) |> 
  select(variable, mean, sd, q5, q95, rhat, ess_bulk, ess_tail) |> 
  filter(variable != "lp__") |>
  mutate(across(c(mean, sd, q5, q95, rhat, ess_bulk, ess_tail), ~round(., 3))) |> 
  kable()

variable	mean	sd	q5	q95	rhat	ess_bulk	ess_tail
Q[1]	0.137	0.317	-0.396	0.672	1.001	20694.09	5373.128
Q[2]	0.103	0.321	-0.425	0.629	1.001	20994.93	5362.172
Q[3]	0.271	0.318	-0.247	0.798	1.000	20676.69	5913.964
Q[4]	0.555	0.313	0.043	1.069	1.000	18730.09	5575.563
Q[5]	-0.120	0.315	-0.636	0.390	1.001	19760.24	5848.199
Q[6]	-0.370	0.312	-0.880	0.145	1.000	16654.60	5972.842
Q[7]	0.286	0.314	-0.231	0.795	1.001	17442.52	6084.769
Q[8]	0.271	0.319	-0.256	0.805	1.000	18199.26	5596.789
Q[9]	0.080	0.314	-0.438	0.584	1.000	19534.73	5983.451
Q[10]	0.118	0.308	-0.386	0.626	1.000	21143.80	5814.923
Q[11]	-0.010	0.321	-0.546	0.510	1.000	20940.00	5531.936
Q[12]	-0.029	0.322	-0.560	0.500	1.001	18276.46	5849.228
Q[13]	-0.105	0.312	-0.609	0.414	1.003	20575.88	5957.570
Q[14]	0.005	0.313	-0.505	0.525	1.001	17541.60	5723.524
Q[15]	-0.215	0.318	-0.740	0.312	1.001	17150.01	5412.980
Q[16]	-0.201	0.315	-0.722	0.315	1.001	17596.06	5120.461
Q[17]	-0.142	0.316	-0.665	0.379	1.000	20718.38	6172.910
Q[18]	-0.860	0.314	-1.384	-0.343	1.000	18745.31	6126.091
Q[19]	-0.161	0.311	-0.666	0.343	1.000	18166.25	6352.717
Q[20]	0.380	0.313	-0.127	0.896	1.000	21072.45	5060.363
sigma	0.997	0.054	0.912	1.092	1.000	13245.07	6385.483

8.3.1 Diagnóstico: Trazas de cadenas

Para hacer diagnósticos, podemos comenzar con las trazas de una cadena para todas las estimaciones de calidad de vino. Cada cadena se inicia con distintos valores aleatorios, pero cumplen en teoría que su distribución de equilibrio es la posterior de interés pues sus transiciones usan el mismo mecanismo.

library(bayesplot)
mcmc_trace(ajuste_vinos_1$draws("Q", format = "df") |> filter(.chain == 1))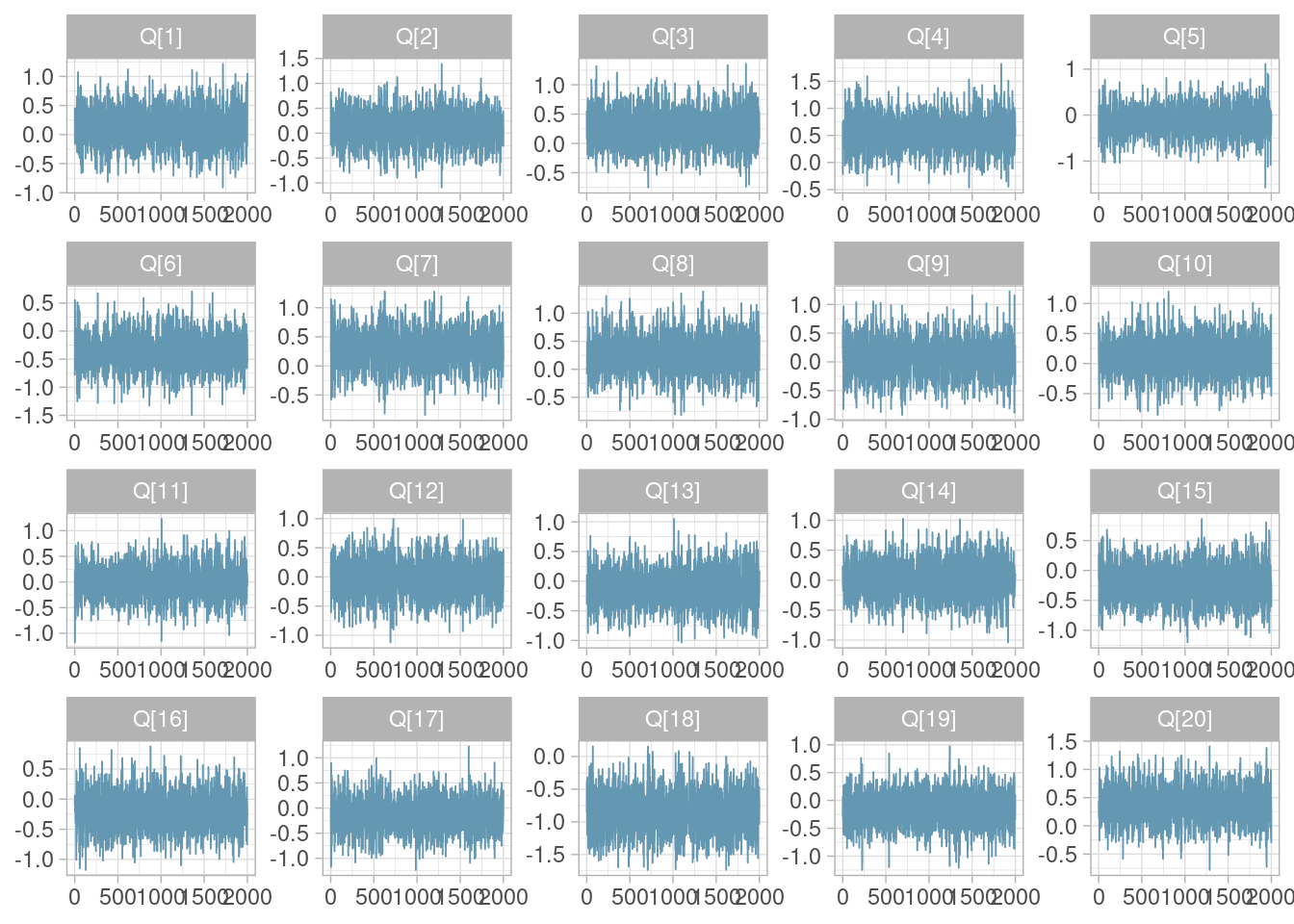

Tip

La traza de una cadena es la gráfica de las simulaciones de cada parámetro. Generalmente buscamos que: no tenga tendencia, que no se quede “atorada” en algunos valores, y que no muestre oscilaciones de baja frecuencia (la cadena “vaga” por los valores que explora).

Si incluímos todas las cadenas, nos fijemos en que todas ellas exploren regiones similares del espacio de parámetros:

color_scheme_set("viridis")
mcmc_trace(ajuste_vinos_1$draws("Q", format = "df"))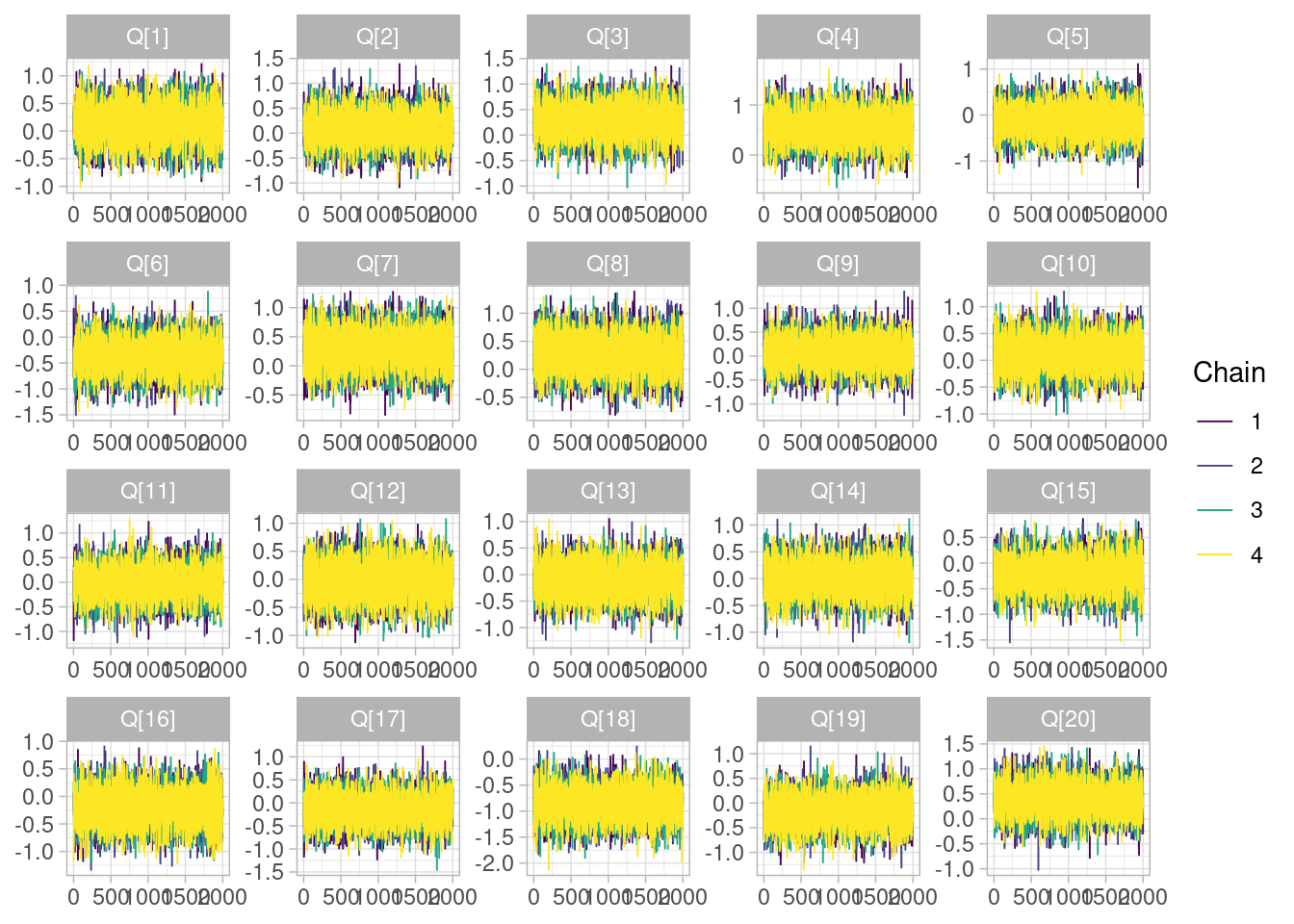 

Lo que no queremos ver es lo siguiente, por ejemplo:

ajuste_vinos_malo <- mod_vinos_1$sample(
  data = datos_lst,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 5,
  iter_sampling = 100,
  refresh = 1000,
  step_size =1 ,
  seed = 123
)

Running MCMC with 4 parallel chains...

Chain 1 WARNING: No variance estimation is 
Chain 1          performed for num_warmup < 20 
Chain 1 Iteration:   1 / 105 [  0%]  (Warmup) 
Chain 1 Iteration:   6 / 105 [  5%]  (Sampling) 
Chain 1 Iteration: 105 / 105 [100%]  (Sampling) 
Chain 2 WARNING: No variance estimation is 
Chain 2          performed for num_warmup < 20 
Chain 2 Iteration:   1 / 105 [  0%]  (Warmup) 
Chain 2 Iteration:   6 / 105 [  5%]  (Sampling) 
Chain 2 Iteration: 105 / 105 [100%]  (Sampling) 
Chain 3 WARNING: No variance estimation is 
Chain 3          performed for num_warmup < 20 
Chain 3 Iteration:   1 / 105 [  0%]  (Warmup) 
Chain 3 Iteration:   6 / 105 [  5%]  (Sampling) 
Chain 3 Iteration: 105 / 105 [100%]  (Sampling) 

Chain 3 Informational Message: The current Metropolis proposal is about to be rejected because of the following issue:

Chain 3 Exception: normal_lpdf: Scale parameter is 0, but must be positive! (in '/tmp/Rtmpor1cYv/model-282661f34b78.stan', line 25, column 2 to column 33)

Chain 3 If this warning occurs sporadically, such as for highly constrained variable types like covariance matrices, then the sampler is fine,

Chain 3 but if this warning occurs often then your model may be either severely ill-conditioned or misspecified.

Chain 3 

Chain 4 WARNING: No variance estimation is 
Chain 4          performed for num_warmup < 20 
Chain 4 Iteration:   1 / 105 [  0%]  (Warmup) 
Chain 4 Iteration:   6 / 105 [  5%]  (Sampling) 
Chain 4 Iteration: 105 / 105 [100%]  (Sampling) 
Chain 1 finished in 0.0 seconds.
Chain 2 finished in 0.0 seconds.
Chain 3 finished in 0.0 seconds.
Chain 4 finished in 0.0 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.0 seconds.
Total execution time: 0.2 seconds.

Warning: 324 of 400 (81.0%) transitions ended with a divergence.
See https://mc-stan.org/misc/warnings for details.

Warning: 2 of 4 chains had an E-BFMI less than 0.3.
See https://mc-stan.org/misc/warnings for details.

color_scheme_set("viridisA")
mcmc_trace(ajuste_vinos_malo$draws("Q", format = "df"))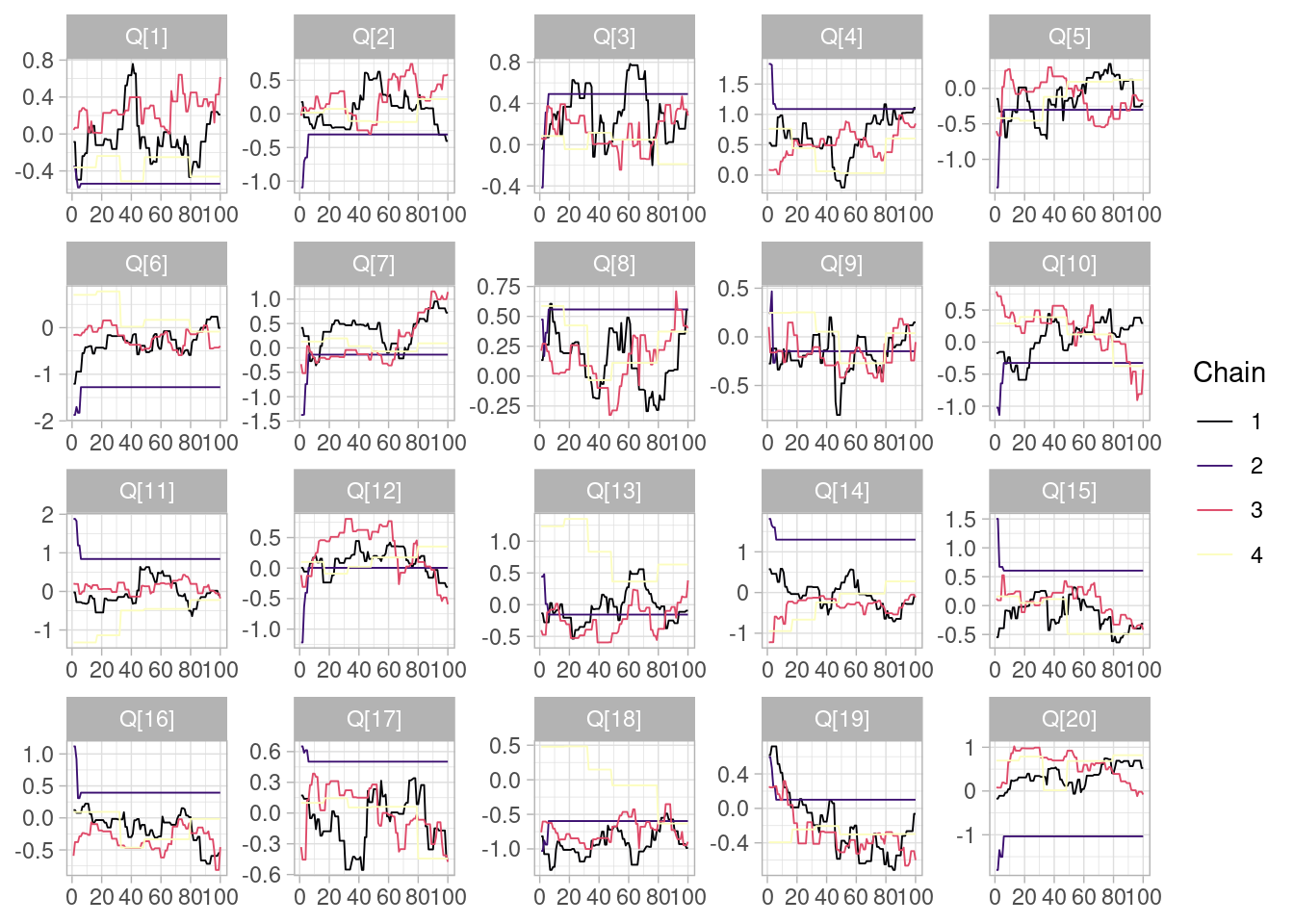 

Hay varios problemas graves:

• Algunas cadenas parecen “atoradas” en ciertos valores
• Algunas cadenas parecen caminatas aleatorias (oscilaciones de baja frecuencia)
• Las cadenas no exploran de manera similar el espacio de parámetros

Traza de cadenas

El diagnóstico de traza consiste en graficar las cadenas de los parámetros en el orden de la iteración. Buscamos ver que:

1. Las cadenas no tienen tendencia o oscilaciones de frecuencia muy baja.
2. Las cadenas no se atoran en valores específicos.
3. Las distintas cadenas exploran de manera similar el espacio de parámetros.

Cuando falla alguna de estas, en el mejor de los casos las cadenas son ineficientes (veremos que requerimos un número mucho mayor de iteraciones), y en el peor de los casos dan resultados sesgados que no son confiables.

8.3.2 Diagnóstico: valores R-hat

Cuando nuestro método de simulación converge a la distribución posterior, esperamos que las cadenas, durante todo su proceso, exploran la misma región del espacio de parámetros.

Podemos entonces considerar, para cada parámetro:

• Cuánta variación hay en cada cadena.
• Qué tan distintas son las cadenas entre ellas.

Esperamos que la variación entre cadenas es chica, y la variación dentro de cada cadena es similar para todas las cadenas. Calculamos entonces un cociente de varianzas: la varianza total sobre todas las simulaciones de todas las cadenas, y el promedio de varianzas de las cadenas. Si las cadenas están explorando regiones similares, esperamos que este cociente de varianzas sea cercano a 1.

Escribiremos ahora esta idea para entender cómo se calculan estas cantidades. Supongamos que cada cadena se denota por \(\theta_m\), para \(M\) cadenas, y las iteraciones de cada cadena son \(\theta_m^{(i)}\) para \(i=1,\ldots, N\) iteraciones. Definimos (ver el manual de Stan o Brooks et al. (2011) por ejemplo) primero la varianza entre cadenas, que es (ojo: usaremos definiciones aproximadas para entender más fácilmente):

\[b=\frac{1}{M-1}\sum_{m=1}^M (\bar{\theta}_m - \bar{\theta})^2\] donde \(\bar{\theta}_m\) es el promedio de las iteraciones de la cadena \(m\), y \(\bar{\theta}\) es el promedio del las \(\bar{\theta}_m\).

Definimos también la varianza dentro de las cadenas, que es el promedio de la varianza de cada cadena:

\[w=\frac{1}{M}\sum_{m=1}^M \frac{1}{N}\sum_{i=1}^N (\theta_m^{(i)} - \bar{\theta}_m)^2\] Finalmente, la \(R\)-hat, o estadística de potencial de reducción de escala, es (para \(N\) grande),

\[\hat{R} = \sqrt{\frac{b+w}{w}}\]

Buscamos entonces que este valor sea cercano a 1. Si es mayor a 1.05, es señal de posibles problemas de convergencia (pocas iteraciones u otras fallas en la convergencia). Si es menor que 1.01, generalmente decimos que “pasamos” esta prueba. Esto no es garantía de que la convergencia se ha alcanzado: la primera razón es que este diagnóstico, por ejemplo, sólo considera media y varianza, de forma que en principio podríamos pasar esta prueba aún cuando las cadenas tengan comportamiento distinto en otras estadísticas de orden más alto (por ejemplo, una cadena que oscila poco y de vez en cuando salta a un atípico vs otra que tiene variación moderada pueden ser similares en medias y varianzas).

En Stan, adicionalmente, se divide cada cadena en dos mitades, y el análisis se hace sobre \(2M\) medias cadenas. Esto ayuda a detectar por ejemplo problemas donde una cadena sube y luego baja, por ejemplo, de modo que puede tener el mismo promedio que otras que exploran correctamente.

Nota: Estas fórmulas pretenden explicar de manera simple el concepto de \(R\)-hat, y son correctas para \(N\) grande, lo cual casi siempre es el caso (al menos \(N\geq 100\)). Puedes consultar una definición más estándar con correcciones por grados de libertad en el manual de Stan o cualquier libro de MCMC.

Diagnóstico de R-hat

El diagnóstico de R-hat compara la varianza dentro de las cadenas y de cadena a cadena. Cuando este valor es relativamente grande (por ejemplo mayor a 1.05), es señal de que las cadenas no han explorado apropiadamente el espacio de parámetros (o decimos que no están “mezclando”). En general, buscamos que este valor sea menor a 1.02.

Se llama también potencial de reducción a escala porque busca indicar cuánto se podría reducir la varianza de la distribución actual si dejáramos correr las cadenas por más iteraciones (pues a largo plazo no debe haber varianza entre cadenas).

En nuestro ejemplo apropiado, observamos valores muy cercanos a 1 para todos los parámetros:

ajuste_vinos_1$summary(c("Q", "sigma")) |> 
  select(variable, mean, sd, q5, q95, rhat, ess_bulk, ess_tail) |> 
  mutate(across(c(mean, sd, q5, q95, rhat, ess_bulk, ess_tail), ~round(., 3))) |> 
  filter(variable != "lp__") |> kable()

variable	mean	sd	q5	q95	rhat	ess_bulk	ess_tail
Q[1]	0.137	0.317	-0.396	0.672	1.001	20694.09	5373.128
Q[2]	0.103	0.321	-0.425	0.629	1.001	20994.93	5362.172
Q[3]	0.271	0.318	-0.247	0.798	1.000	20676.69	5913.964
Q[4]	0.555	0.313	0.043	1.069	1.000	18730.09	5575.563
Q[5]	-0.120	0.315	-0.636	0.390	1.001	19760.24	5848.199
Q[6]	-0.370	0.312	-0.880	0.145	1.000	16654.60	5972.842
Q[7]	0.286	0.314	-0.231	0.795	1.001	17442.52	6084.769
Q[8]	0.271	0.319	-0.256	0.805	1.000	18199.26	5596.789
Q[9]	0.080	0.314	-0.438	0.584	1.000	19534.73	5983.451
Q[10]	0.118	0.308	-0.386	0.626	1.000	21143.80	5814.923
Q[11]	-0.010	0.321	-0.546	0.510	1.000	20940.00	5531.936
Q[12]	-0.029	0.322	-0.560	0.500	1.001	18276.46	5849.228
Q[13]	-0.105	0.312	-0.609	0.414	1.003	20575.88	5957.570
Q[14]	0.005	0.313	-0.505	0.525	1.001	17541.60	5723.524
Q[15]	-0.215	0.318	-0.740	0.312	1.001	17150.01	5412.980
Q[16]	-0.201	0.315	-0.722	0.315	1.001	17596.06	5120.461
Q[17]	-0.142	0.316	-0.665	0.379	1.000	20718.38	6172.910
Q[18]	-0.860	0.314	-1.384	-0.343	1.000	18745.31	6126.091
Q[19]	-0.161	0.311	-0.666	0.343	1.000	18166.25	6352.717
Q[20]	0.380	0.313	-0.127	0.896	1.000	21072.45	5060.363
sigma	0.997	0.054	0.912	1.092	1.000	13245.07	6385.483

En nuestro ejemplo “malo”, obtenemos valores no aceptabels de R-hat para varios parámetros.

ajuste_vinos_malo$summary(c("Q", "sigma")) |> 
  select(variable, mean, sd, q5, q95, rhat, ess_bulk, ess_tail) |> 
  mutate(across(c(mean, sd, q5, q95, rhat, ess_bulk, ess_tail), ~round(., 3))) |> 
  filter(variable != "lp__") |> kable()

variable	mean	sd	q5	q95	rhat	ess_bulk	ess_tail
Q[1]	-0.167	0.345	-0.538	0.427	2.367	5.335	4.502
Q[2]	-0.012	0.289	-0.306	0.556	1.633	7.010	4.670
Q[3]	0.226	0.246	-0.188	0.596	1.379	9.802	14.937
Q[4]	0.651	0.385	0.032	1.088	1.596	7.207	12.047
Q[5]	-0.173	0.253	-0.547	0.191	1.441	8.933	58.601
Q[6]	-0.387	0.626	-1.277	0.704	2.367	5.372	4.348
Q[7]	0.084	0.364	-0.291	0.812	1.340	10.165	27.683
Q[8]	0.272	0.254	-0.180	0.558	1.372	9.580	18.466
Q[9]	-0.117	0.188	-0.377	0.247	1.689	13.208	30.165
Q[10]	0.004	0.347	-0.460	0.496	1.557	7.600	25.190
Q[11]	0.068	0.618	-1.137	0.840	2.724	5.072	7.003
Q[12]	0.119	0.270	-0.245	0.625	1.237	14.834	42.161
Q[13]	0.089	0.491	-0.489	1.235	1.868	6.388	28.327
Q[14]	0.172	0.736	-0.780	1.299	2.064	5.741	18.739
Q[15]	0.082	0.407	-0.491	0.605	2.109	5.718	17.270
Q[16]	-0.055	0.339	-0.548	0.394	1.711	6.843	25.826
Q[17]	0.104	0.310	-0.444	0.502	1.811	6.325	20.519
Q[18]	-0.562	0.429	-1.076	0.479	1.959	6.022	28.327
Q[19]	-0.162	0.281	-0.600	0.248	1.561	7.410	41.928
Q[20]	0.122	0.737	-1.036	0.922	1.949	6.030	4.348
sigma	0.958	0.239	0.751	1.092	1.571	7.369	8.522

Nota: si algunos parámetros tienen valores R-hat cercanos a 1 pero otros no, en general no podemos confiar en los resultados de las simulaciones. Esto es señal de problemas de convergencia y deben ser diagnosticados.

8.3.3 Diagnóstico: Tamaño de muestra efectivo

Las simulaciones de MCMC típicamente están autocorrelacionadas (pues comenzamos en una región y muchas veces nos movemos poco). Esto significa que la cantidad de información de \(N\) simulaciones MCMC no es la misma que la que obtendríamos con \(N\) simulaciones independientes de la posterior.

Este concepto también se usa en muestreo: por ejemplo, existe menos información en una muestra de 100 personas que fueron muestreadas por conglomerados de 50 casas (por ejemplo, seleccionando al azar hogares y luego a dos adultos dentro de cada hogar) que seleccionar 100 hogares y escoger a un al azar un adulto de cada hogar. La segunda muestra tienen más información de la población, pues en la primera muestra parte de la información es “compartida” por el hecho de vivir en el mismo hogar. Para encontrar un número “efectivo” de muestra que haga comparables estos dos diseños, comparamos la varianza que obtendríamos del estimador de interes en cada caso. Si consideramos como base el segundo diseño (muestro aleatorio independiente), el primer diseño tendrá más varianza. Eso quiere decir que para que hubiera la misma varianza en los dos diseños, bastaría una muestra más chica (digamos 60 hogares) del segundo diseño independiente. Decimos que el tamaño efectivo de muestra del primer diseño es de 60 personas (el caso donde las varianzas de los dos diseños son iguales).

En el caso de series de tiempo, tenemos que considerar autocorrelación en la serie. Supongamos que quisiéramos estimar la media de una serie de tiempo (suponemos que a largo plazo el promedio de la serie de tiempo es una constante finita). Una muestra con autocorrelación alta produce malos estimadores de esta media incluso para tamaños de muestra relativamente grande:

set.seed(123)
mu_verdadera <- 10
simular_series <- function(T = 500, num_series = 100, ar = 0.9){
  map_df(1:num_series, function(rep){
    serie <- 10 + arima.sim(n = T, list(ar = ar), n.start = 200, sd = sqrt(1-ar^2))
    tibble(t = 1:T, serie = serie, serie_id = rep, ar = ar)
  })
}
series_1_tbl <- simular_series(T= 200, n = 4, ar = 0.80)
series_2_tbl <- simular_series(T= 200, n = 4, ar = 0.00001)
series_tbl <- bind_rows(series_1_tbl, series_2_tbl)
series_tbl |> 
  ggplot(aes(t, serie, group = serie_id, colour = factor(serie_id))) + 
  geom_line(alpha = 0.9) + 
  geom_hline(yintercept = mu_verdadera, linetype = 2) + 
  facet_wrap(~ar, ncol = 1)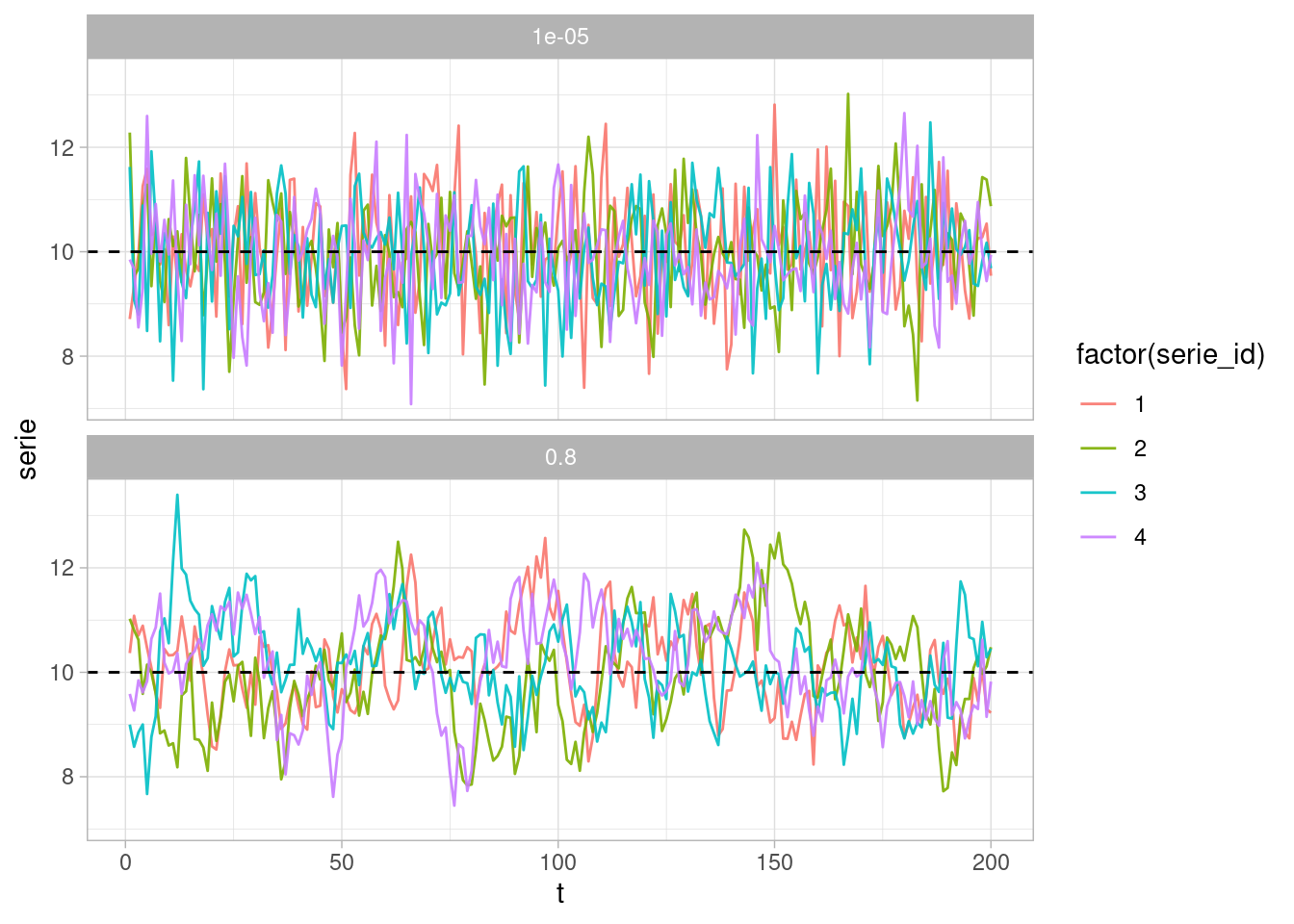

Calculamos las medias para un ejemplo con autocorrelación y otro sin ellas:

series_95_tbl <- simular_series(T= 300, n = 500, ar = 0.80) 
series_05_tbl <- simular_series(T= 300, n = 500, ar = 0.00001) 
series_tbl <- bind_rows(series_95_tbl, series_05_tbl)
series_tbl |> group_by(serie_id, ar) |> 
  summarise(media = mean(serie)) |> 
  ggplot(aes(media)) + geom_histogram() + 
  geom_vline(xintercept = mu_verdadera, linetype = 2) + 
  labs(title = "Distribución de medias de series de tiempo") +
  facet_wrap(~ar)

`summarise()` has grouped output by 'serie_id'. You can override using the
`.groups` argument.
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.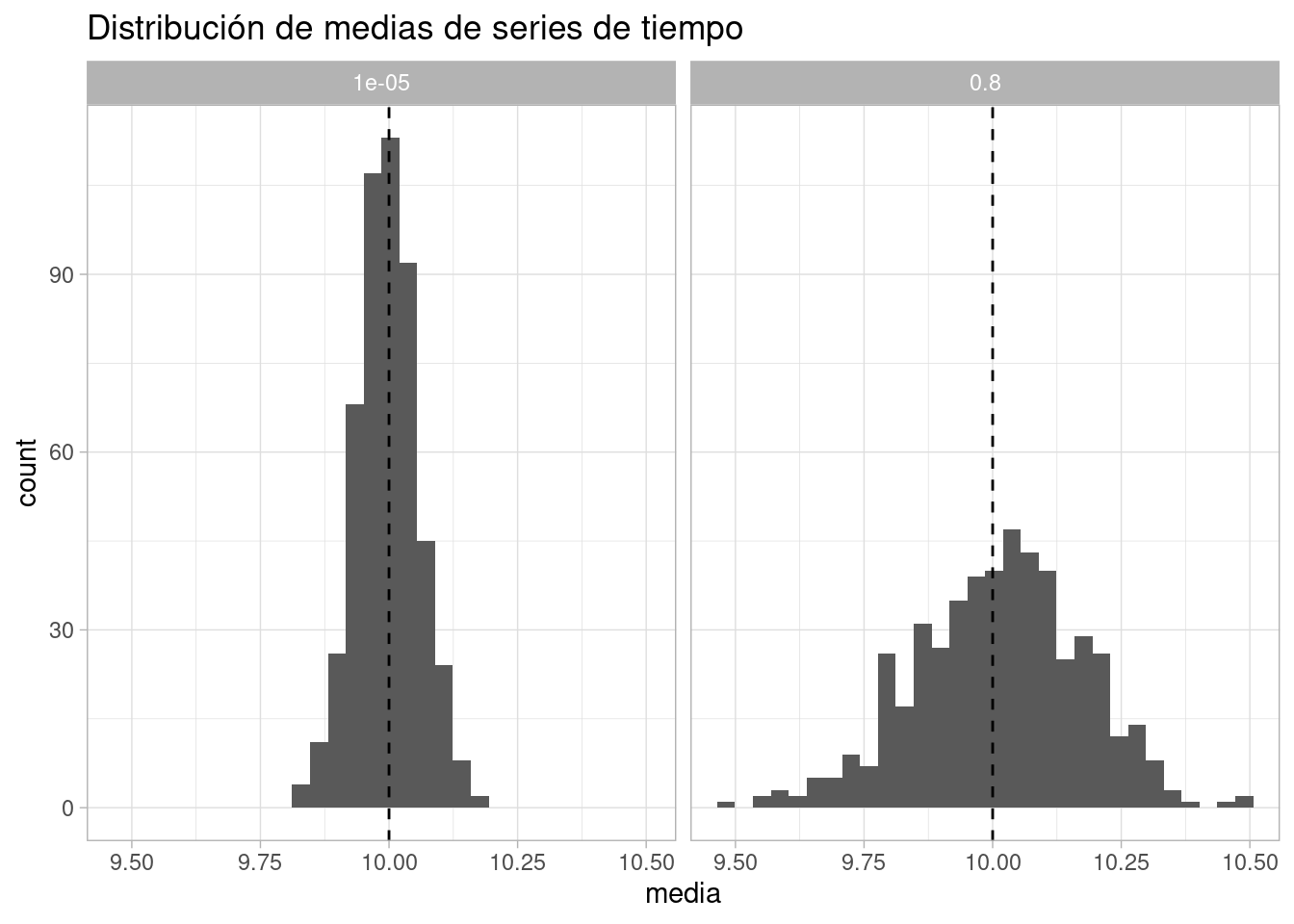

Y vemos que la precisión de la estimación cuando la correlación es relativamente baja es mucho más alta que cuando la correlación es alta. ¿Cuál es el tamaño efectivo de muestra para series con autocorrelación ar= 0.8? Vemos que es aproximadamente 35, o dicho de otra manera, la serie sin correlación nos da casi 10 veces más información por observación que la correlacionada:

series_95_tbl <- simular_series(T= 300, n = 1000, ar = 0.8) 
series_05_tbl <- simular_series(T= 35, n = 1000, ar = 0.00001) 
series_tbl <- bind_rows(series_95_tbl, series_05_tbl)
series_tbl |> group_by(serie_id, ar) |> 
  summarise(media = mean(serie)) |> 
  ggplot(aes(media)) + geom_histogram() + 
  geom_vline(xintercept = mu_verdadera, linetype = 2) + 
  labs(title = "Distribución de medias de series de tiempo") +
  facet_wrap(~ar)

`summarise()` has grouped output by 'serie_id'. You can override using the
`.groups` argument.
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.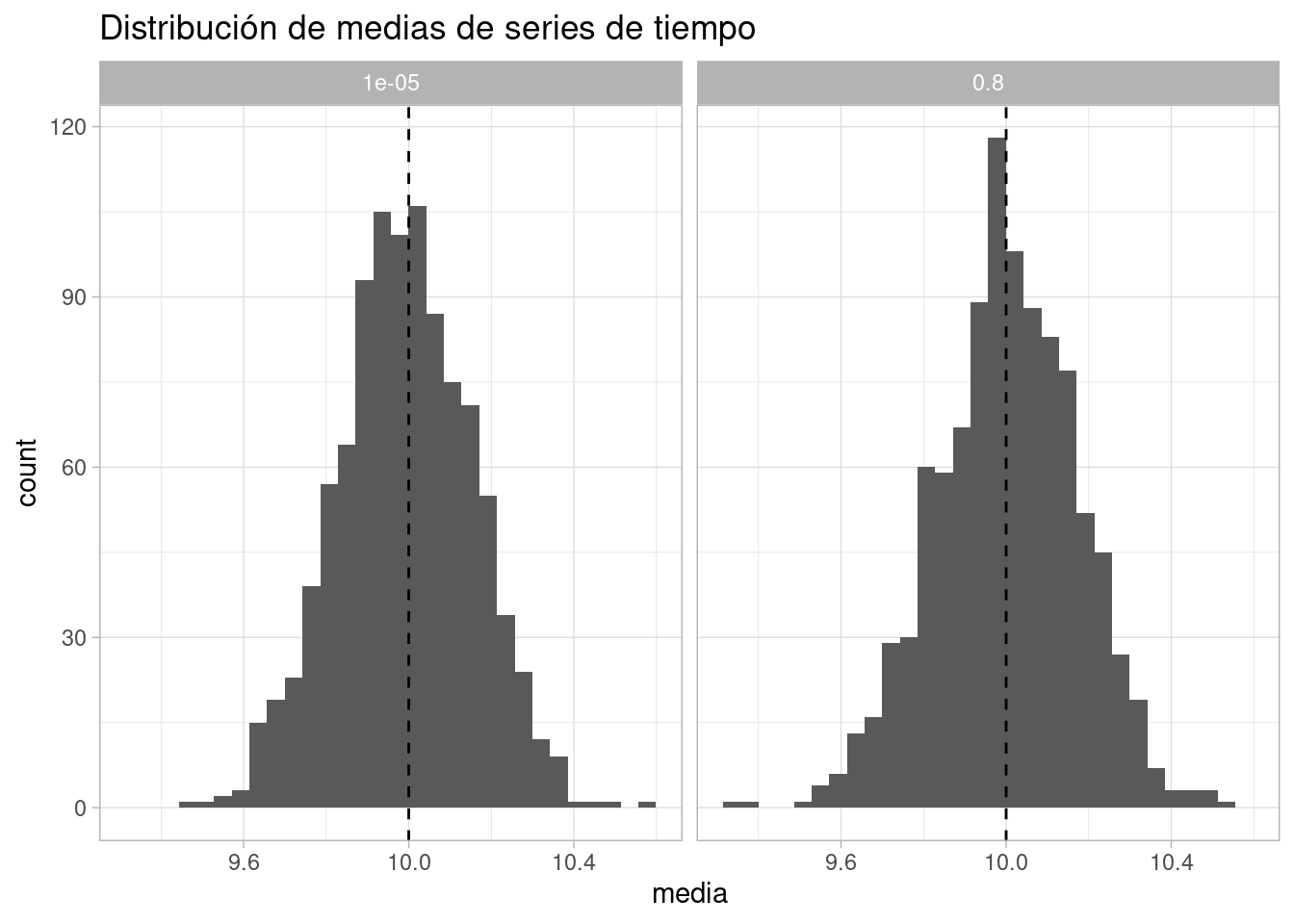

Es posible hacer una estimación teórica del tamaño efectivo de muestra. Para esto, podemos notar que la varianza del promedio de una serie de tiempo depende de la estructura de autocorrelación. Supondremos que la serie de tiempo es estacionaria y cada \(y_t\) tiene varianza \(\sigma^2\) y correlación \(\rho\) con \(y_{t-1}\). Entonces:

\[Var(\bar{y})=\frac{1}{n^2}\text{Var} \left(\sum_{t=1}^n y_t \right) = \frac{n\sigma^2}{n^2}\sum_{t=1}^n \text{Var}(y_t) + \frac{2\sigma^2}{n^2}\sum_{t=1}^{n-1}\sum_{s=t+1}^n\text{Corr}(y_t, y_s)\]

Que se simplifica a (para \(n\) grande):

\[\text{Var}(\bar{y}) = \frac{\sigma^2}{n} + \frac{2\sigma^2}{n}\sum_{h=1}^{n-1}(1-h/n)\rho_{h} \approx \frac{\sigma^2}{n}\left (1+2\sum_{h=1}^{n-1}\rho_t\right )\] Si suponemos \(\rho_h = \text{corr}(y_t, y_{t+h})\) para cualquier \(t\). En nuestro caso anterior, el factor de corrección es aproximadamente:

1 + 2*(0.8)^(1:1000) |> sum()

[1] 9

Tamaño efectivo de muestra

Si hacemos \(N\) iteraciones en una cadena estacionaria con función de autocorrelación \(\rho_h\), el tamaño efectivo de muestra teórico se define como

\[N_{eff} = \frac{N}{1 + 2\sum_{h=1}^{\infty}\rho_h}\]

Si pudiéramos hacer simulaciones independientes de la posterior, \(N_{eff}\) es el tamaño de muestra requerido para obtener la misma información que la cadena autocorrelacionada de tamaño \(N\). Usualmente, aunque no siempre, \(N_{eff}<N\) para cadenas de MCMC.

Observaciones:

1. Esta es una definición teórica para entender el concepto. Para ver cómo se estima en la práctica puedes consultar el manual de Stan o (Brooks et al. 2011).
2. En algunos muestreadores que dan pasos cortos como en los ejemplos de Metropolis-Hastings que vimos, a veces es necesario hacer cientos de miles de iteraciones para obtener un tamaño efectivo de muestra apropiado para hacer inferencia. Stan generalmente obtiene tamaños efectivos de muestra mucho más altos con menos iteraciones (aunque cada iteración es más costosa).
3. Considerando experiencia y teoría, tamaños efectivos de muestra mínimos se considera de 400 o más (ver aquí).

En nuestro ejemplo, tenemos tamaños de muestra efectivos satisfactorios:

ajuste_vinos_1$summary(c("Q", "sigma")) |> 
  select(variable, mean, sd, q5, q95, rhat, contains("ess")) |> 
  mutate(across(c(mean, sd, q5, q95, rhat, ess_bulk, ess_tail), ~round(., 3))) |> 
  filter(variable != "lp__") |> kable()

variable	mean	sd	q5	q95	rhat	ess_bulk	ess_tail
Q[1]	0.137	0.317	-0.396	0.672	1.001	20694.09	5373.128
Q[2]	0.103	0.321	-0.425	0.629	1.001	20994.93	5362.172
Q[3]	0.271	0.318	-0.247	0.798	1.000	20676.69	5913.964
Q[4]	0.555	0.313	0.043	1.069	1.000	18730.09	5575.563
Q[5]	-0.120	0.315	-0.636	0.390	1.001	19760.24	5848.199
Q[6]	-0.370	0.312	-0.880	0.145	1.000	16654.60	5972.842
Q[7]	0.286	0.314	-0.231	0.795	1.001	17442.52	6084.769
Q[8]	0.271	0.319	-0.256	0.805	1.000	18199.26	5596.789
Q[9]	0.080	0.314	-0.438	0.584	1.000	19534.73	5983.451
Q[10]	0.118	0.308	-0.386	0.626	1.000	21143.80	5814.923
Q[11]	-0.010	0.321	-0.546	0.510	1.000	20940.00	5531.936
Q[12]	-0.029	0.322	-0.560	0.500	1.001	18276.46	5849.228
Q[13]	-0.105	0.312	-0.609	0.414	1.003	20575.88	5957.570
Q[14]	0.005	0.313	-0.505	0.525	1.001	17541.60	5723.524
Q[15]	-0.215	0.318	-0.740	0.312	1.001	17150.01	5412.980
Q[16]	-0.201	0.315	-0.722	0.315	1.001	17596.06	5120.461
Q[17]	-0.142	0.316	-0.665	0.379	1.000	20718.38	6172.910
Q[18]	-0.860	0.314	-1.384	-0.343	1.000	18745.31	6126.091
Q[19]	-0.161	0.311	-0.666	0.343	1.000	18166.25	6352.717
Q[20]	0.380	0.313	-0.127	0.896	1.000	21072.45	5060.363
sigma	0.997	0.054	0.912	1.092	1.000	13245.07	6385.483

• Nótese que versiones más recientes de Stan reportan dos tamaños efectivos de muestra (ESS), uno para cantidades que dependen del centro de la distribución, como la media y mediana (bulk ESS, que es similar a la definición que vimos arriba, pero usando valores normalizados por rango), y otro para cantidades que dependen de las colas, como percentiles extremos (tail ESS, que estima el tamaño de muestra efectivo para los percentiles 5% y 95% ). En este caso, ambos son altos.

Finalmente, podemos checar el error montecarlo, que es error de estimación usual

ajuste_vinos_1$summary(c("Q", "sigma")) |> 
  select(variable, mean, sd, q5, q95, rhat, contains("ess")) |>
  mutate(across(c(mean, sd, q5, q95, rhat, ess_bulk, ess_tail), ~round(., 3))) |> 
  filter(variable != "lp__") |> kable()

variable	mean	sd	q5	q95	rhat	ess_bulk	ess_tail
Q[1]	0.137	0.317	-0.396	0.672	1.001	20694.09	5373.128
Q[2]	0.103	0.321	-0.425	0.629	1.001	20994.93	5362.172
Q[3]	0.271	0.318	-0.247	0.798	1.000	20676.69	5913.964
Q[4]	0.555	0.313	0.043	1.069	1.000	18730.09	5575.563
Q[5]	-0.120	0.315	-0.636	0.390	1.001	19760.24	5848.199
Q[6]	-0.370	0.312	-0.880	0.145	1.000	16654.60	5972.842
Q[7]	0.286	0.314	-0.231	0.795	1.001	17442.52	6084.769
Q[8]	0.271	0.319	-0.256	0.805	1.000	18199.26	5596.789
Q[9]	0.080	0.314	-0.438	0.584	1.000	19534.73	5983.451
Q[10]	0.118	0.308	-0.386	0.626	1.000	21143.80	5814.923
Q[11]	-0.010	0.321	-0.546	0.510	1.000	20940.00	5531.936
Q[12]	-0.029	0.322	-0.560	0.500	1.001	18276.46	5849.228
Q[13]	-0.105	0.312	-0.609	0.414	1.003	20575.88	5957.570
Q[14]	0.005	0.313	-0.505	0.525	1.001	17541.60	5723.524
Q[15]	-0.215	0.318	-0.740	0.312	1.001	17150.01	5412.980
Q[16]	-0.201	0.315	-0.722	0.315	1.001	17596.06	5120.461
Q[17]	-0.142	0.316	-0.665	0.379	1.000	20718.38	6172.910
Q[18]	-0.860	0.314	-1.384	-0.343	1.000	18745.31	6126.091
Q[19]	-0.161	0.311	-0.666	0.343	1.000	18166.25	6352.717
Q[20]	0.380	0.313	-0.127	0.896	1.000	21072.45	5060.363
sigma	0.997	0.054	0.912	1.092	1.000	13245.07	6385.483

8.4 Extendiendo el modelo de variable latente

Ahora continuamos con nuestro modelo de calidad de vinos. Incluímos el origen del vino (que tiene dos niveles). La idea es que el origen, si vemos en el diagrama original, puede ser una variable de confusión entre calidad y score (pues afecta a calidad y también potencialmente al score). Adicionalmente, el origen no tiene puerta trasera, así que podemos examinar su efecto total sobre el score de los vinos. Estratificamos de la manera más simple, incluyendo origen en nuestra regresión:

wines_2012 <- wines_2012 |> mutate(origen_num = ifelse(wine.amer == 1, 1, 2))
wines_2012 |> select(wine.amer, origen_num) |> unique()

# A tibble: 2 × 2
  wine.amer origen_num
      <dbl>      <dbl>
1         1          1
2         0          2

n_jueces <- length(unique(wines_2012$juez_num))
n_vinos <- length(unique(wines_2012$vino_num))
n_origen <- length(unique(wines_2012$origen_num))
c("num_vinos" = n_vinos, "num_jueces" = n_jueces, "num_datos" = nrow(wines_2012))

 num_vinos num_jueces  num_datos 
        20          9        180 

mod_vinos_2 <-cmdstan_model("./src/vinos-2.stan")
print(mod_vinos_2)

data {
  int<lower=0> N; //número de calificaciones
  int<lower=0> n_vinos; //número de vinos
  int<lower=0> n_jueces; //número de jueces
  int<lower=0> n_origen; //número de jueces
  vector[N]  S;
  array[N]  int juez;
  array[N]  int vino;
  array[N]  int origen;
}

parameters {
  vector[n_vinos] Q;
  vector[n_origen] O;
  real <lower=0> sigma;
}

transformed parameters {
  vector[N] media_score;
  // determinístico dado parámetros
  for (i in 1:N){
    media_score[i] = Q[vino[i]] + O[origen[i]];
  }
}

model {
  // partes no determinísticas
  S ~ normal(media_score, sigma);
  Q ~ std_normal();
  O ~ std_normal();
  sigma ~ exponential(1);
}

generated quantities {
  real dif_origen;
  dif_origen = O[1] - O[2];
}

datos_lst <- list(
  N = nrow(wines_2012),
  n_vinos = n_vinos,
  n_jueces = n_jueces,
  n_origen = n_origen,
  S = wines_2012$score_est,
  vino = wines_2012$vino_num,
  juez = wines_2012$juez_num,
  origen = wines_2012$origen_num
)
ajuste_vinos_2 <- mod_vinos_2$sample(
  data = datos_lst,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 1000,
  iter_sampling = 2000,
  refresh = 1000,
  step_size = 0.1,
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 1 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 1 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 2 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 2 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 2 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 3 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 3 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 3 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 4 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 4 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 4 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 1 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 2 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 3 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 4 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 1 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 3 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 1 finished in 0.6 seconds.
Chain 3 finished in 0.6 seconds.
Chain 2 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 2 finished in 0.6 seconds.
Chain 4 finished in 0.6 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.6 seconds.
Total execution time: 0.8 seconds.

ajuste_vinos_2$summary(c("O", "Q", "sigma")) |> 
  select(variable, mean, sd, q5, q95, rhat, contains("ess")) |>
  mutate(across(c(mean, sd, q5, q95, rhat, ess_bulk, ess_tail), ~round(., 3))) |> 
  filter(variable != "lp__") |> kable()

variable	mean	sd	q5	q95	rhat	ess_bulk	ess_tail
O[1]	-0.066	0.290	-0.543	0.421	1.002	2287.306	3321.151
O[2]	0.106	0.351	-0.465	0.679	1.001	2484.077	3858.430
Q[1]	0.197	0.409	-0.471	0.878	1.001	3942.153	5029.018
Q[2]	0.007	0.447	-0.729	0.725	1.001	3855.171	5170.915
Q[3]	0.332	0.415	-0.364	1.006	1.001	4170.358	5201.923
Q[4]	0.458	0.447	-0.276	1.180	1.001	3678.397	5085.397
Q[5]	-0.223	0.448	-0.952	0.514	1.001	3854.360	5259.621
Q[6]	-0.307	0.412	-0.976	0.366	1.001	4109.770	5083.645
Q[7]	0.198	0.446	-0.534	0.928	1.001	3981.338	5487.974
Q[8]	0.330	0.410	-0.344	1.015	1.000	4160.583	5196.431
Q[9]	0.140	0.411	-0.536	0.821	1.001	3925.106	5383.750
Q[10]	0.182	0.409	-0.489	0.871	1.000	4198.558	4953.803
Q[11]	0.051	0.409	-0.626	0.711	1.001	3835.440	5195.758
Q[12]	0.028	0.414	-0.648	0.707	1.001	4066.563	4891.343
Q[13]	-0.046	0.414	-0.733	0.619	1.000	3731.818	4772.284
Q[14]	-0.083	0.448	-0.814	0.656	1.001	3660.288	4800.175
Q[15]	-0.315	0.448	-1.052	0.423	1.000	4042.565	5126.763
Q[16]	-0.139	0.416	-0.818	0.540	1.000	3953.433	5064.421
Q[17]	-0.083	0.414	-0.770	0.595	1.000	4124.527	5544.165
Q[18]	-0.799	0.409	-1.464	-0.126	1.001	4042.865	4892.500
Q[19]	-0.259	0.447	-0.996	0.480	1.001	3741.120	5044.906
Q[20]	0.287	0.445	-0.439	1.027	1.001	3701.595	5366.897
sigma	0.998	0.056	0.911	1.094	1.000	9688.425	6351.040

Todo parece bien con los diagnósticos. Podemos graficar las estimaciones (nota: aquí estan intervalos de 50% y 90%):

library(bayesplot)
color_scheme_set("red")
mcmc_intervals(ajuste_vinos_2$draws(c("Q", "O", "sigma")))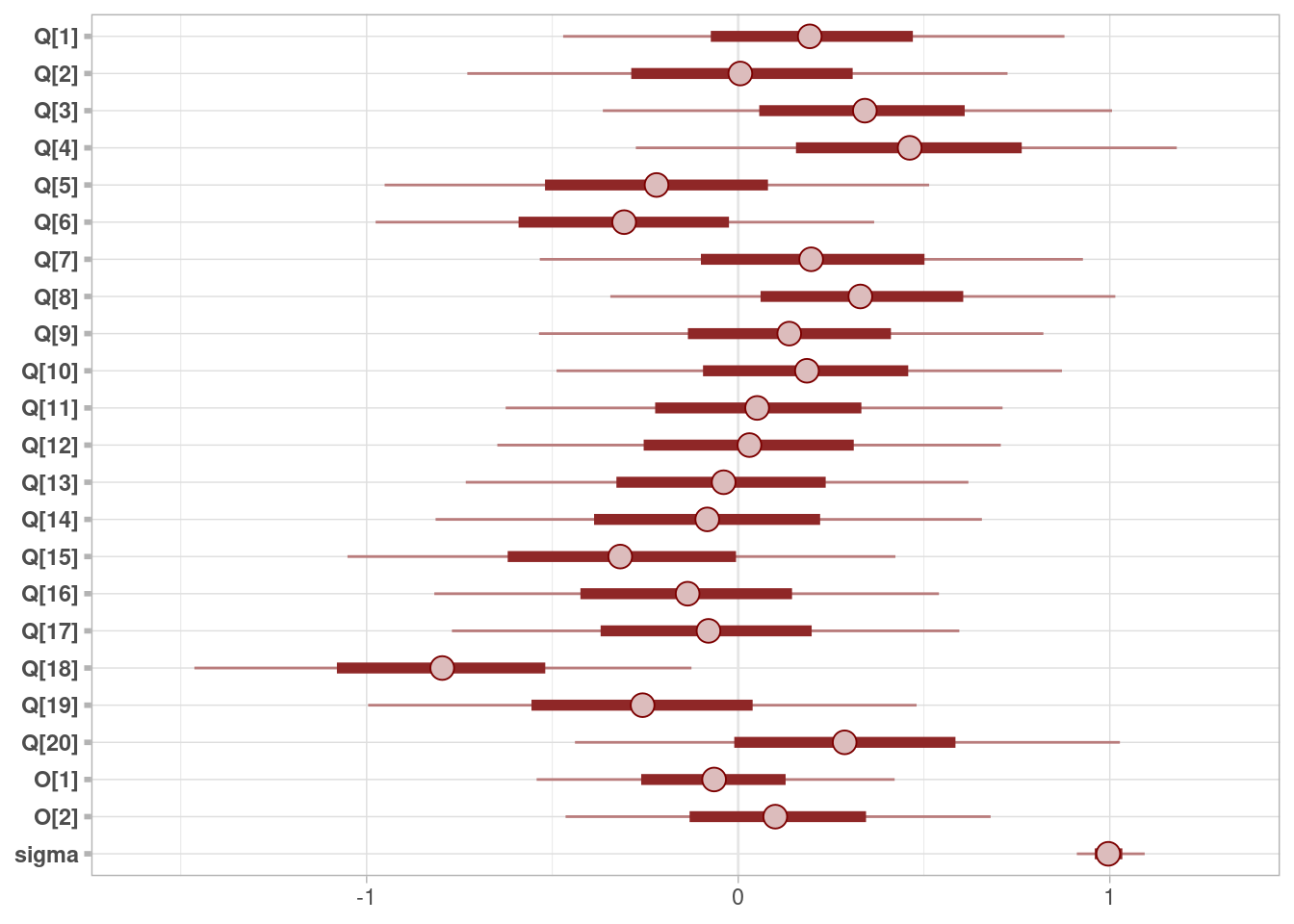

• Parece no haber mucha diferencia en calidad debida origen del vinos (tienen relativamente poca variabilidad y están traslapadas: aunque podríamos mejor calcular el contraste si queremos examinar esto con más cuidado).

Todo parece ir bien, así que podemos expandir el modelo para incluir la forma de calificar de los jueces. Esto no es necesario (los jueces son una causa adicional que afecta el score), pero puede mejorar nuestras estimaciones.

Para estratificar por estas variables, tenemos que separarnos un poco de efectos adivitivos. Una razón importante por la que varían las calificaciones es que hay jueces que son más duros que otros, o que discriminan más qué otros. Esto es usual también cuando pensamos que los jueces son reactivos que las personas contestan: existen reactivos más difíciles que otros, y también discriminan de diferente manera.

En primer lugar, definimos un nivel general \(H\) que indica qué tan alto o bajo califica un juez en general. Adicionalmente, incluímos un parámetro de discriminación \(D\) de los jueces, que indica qué tanto del rango de la escala usa cada juez El modelo para el valor esperado del Score de un vino \(i\) calificado por el juez \(j\) es:

\[\mu_{i} = Q_{vino(i)} + O_{origen(i)} - H_{juez(i)}\] Podemos pensar que el valor \(H\) de cada juez es qué tan duro es en sus calificaciones. Para cada vino, un juez con valor alto de \(H\) tendrá a calificar más bajo un vino de misma calidad y origen que otro juez con un valor más bajo de \(H\). Podemos incluír un parámetro de discriminación \(D\) para cada juez, que indica qué tanto del rango de la escala usa cada juez de la siguiente forma:

\[\mu_{i} = (Q_{vino(i)} + O_{origen(i)} - H_{juez(i)})D_{juez(i)}\] Un juez con valor alto de \(D\) es más extremo en sus calificaciones: un vino por arriba de su promedio lo califica más alto en la escala, y un vino por debajo de su promedio lo califica más bajo. El extremo es que \(D=0\), que quiere decir que el juez tiende a calificar a todos los vinos con un score.

mod_vinos_3 <-cmdstan_model("./src/vinos-3.stan")
print(mod_vinos_3)

data {
  int<lower=0> N; //número de calificaciones
  int<lower=0> n_vinos; //número de vinos
  int<lower=0> n_jueces; //número de jueces
  int<lower=0> n_origen; //número de jueces
  vector[N]  S;
  array[N]  int juez;
  array[N]  int vino;
  array[N]  int origen;
}

parameters {
  vector[n_vinos] Q;
  vector[n_origen] O;
  vector[n_jueces] H;
  vector<lower=0>[n_jueces] D;

  real <lower=0> sigma;
}

transformed parameters {
  vector[N] media_score;
  // determinístico dado parámetros
  for (i in 1:N){
    media_score[i] = (Q[vino[i]] + O[origen[i]] - H[juez[i]]) * D[juez[i]];
  }
}

model {
  // partes no determinísticas
  S ~ normal(media_score, sigma);
  Q ~ std_normal();
  O ~ std_normal();
  H ~ std_normal();
  D ~ std_normal();
  sigma ~ exponential(1);
}

generated quantities {
  real dif_origen;
  dif_origen = O[1] - O[2];
}

datos_lst <- list(
  N = nrow(wines_2012),
  n_vinos = n_vinos,
  n_jueces = n_jueces,
  n_origen = n_origen,
  S = wines_2012$score_est,
  vino = wines_2012$vino_num,
  juez = wines_2012$juez_num,
  origen = wines_2012$origen_num
)
ajuste_vinos_3 <- mod_vinos_3$sample(
  data = datos_lst,
  chains = 4,
  parallel_chains = 4,
  iter_warmup = 1000,
  iter_sampling = 2000,
  refresh = 1000,
  step_size = 0.1,
)

Running MCMC with 4 parallel chains...

Chain 1 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 2 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 3 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 4 Iteration:    1 / 3000 [  0%]  (Warmup) 
Chain 1 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 1 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 2 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 2 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 3 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 3 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 4 Iteration: 1000 / 3000 [ 33%]  (Warmup) 
Chain 4 Iteration: 1001 / 3000 [ 33%]  (Sampling) 
Chain 1 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 2 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 3 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 4 Iteration: 2000 / 3000 [ 66%]  (Sampling) 
Chain 1 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 2 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 4 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 1 finished in 1.5 seconds.
Chain 2 finished in 1.5 seconds.
Chain 4 finished in 1.5 seconds.
Chain 3 Iteration: 3000 / 3000 [100%]  (Sampling) 
Chain 3 finished in 1.5 seconds.

All 4 chains finished successfully.
Mean chain execution time: 1.5 seconds.
Total execution time: 1.7 seconds.

Checamos diagnósticos:

ajuste_vinos_3$summary(c("O", "Q", "H", "D", "sigma")) |> 
  select(variable, mean, sd, q5, q95, rhat, contains("ess")) |>
  mutate(across(c(mean, sd, q5, q95, rhat, ess_bulk, ess_tail), ~round(., 3))) |> 
  filter(variable != "lp__") |> kable()

variable	mean	sd	q5	q95	rhat	ess_bulk	ess_tail
O[1]	-0.115	0.447	-0.859	0.629	1.002	3518.843	4790.784
O[2]	0.198	0.476	-0.572	0.986	1.001	3963.128	5271.349
Q[1]	0.366	0.562	-0.543	1.315	1.000	5657.887	5719.280
Q[2]	0.168	0.586	-0.779	1.132	1.000	5514.261	5765.562
Q[3]	0.508	0.537	-0.369	1.377	1.000	6854.468	5604.398
Q[4]	0.825	0.579	-0.111	1.800	1.000	6452.743	5446.307
Q[5]	-0.483	0.558	-1.385	0.451	1.001	6299.704	5695.944
Q[6]	-0.830	0.593	-1.783	0.171	1.000	4716.862	5114.054
Q[7]	0.229	0.602	-0.753	1.229	1.000	4749.244	6033.222
Q[8]	0.618	0.553	-0.274	1.552	1.001	6631.817	5578.857
Q[9]	0.278	0.556	-0.642	1.179	1.000	5940.039	5748.859
Q[10]	0.313	0.531	-0.568	1.172	1.000	6559.060	5848.707
Q[11]	0.183	0.535	-0.708	1.054	1.000	6569.389	6443.012
Q[12]	-0.079	0.537	-0.941	0.807	1.000	6281.310	5903.469
Q[13]	0.052	0.549	-0.860	0.940	1.001	6563.927	5507.827
Q[14]	-0.158	0.558	-1.077	0.753	1.001	6874.838	5893.450
Q[15]	-0.521	0.584	-1.498	0.422	1.001	5853.924	5734.059
Q[16]	-0.121	0.565	-1.036	0.815	1.001	5233.317	5555.469
Q[17]	0.103	0.562	-0.845	1.007	1.001	5025.607	5096.996
Q[18]	-1.507	0.552	-2.424	-0.608	1.000	5907.052	5459.271
Q[19]	-0.367	0.561	-1.292	0.545	1.001	6738.238	6061.758
Q[20]	0.482	0.569	-0.445	1.408	1.001	5687.180	5521.888
H[1]	0.619	0.586	-0.269	1.601	1.000	6123.319	4979.950
H[2]	-0.274	0.437	-0.998	0.424	1.001	4060.809	4583.991
H[3]	-0.469	0.734	-1.656	0.745	1.000	6648.205	5243.692
H[4]	1.233	0.601	0.322	2.271	1.000	5632.281	5695.773
H[5]	-1.779	0.618	-2.853	-0.815	1.000	6082.938	5816.825
H[6]	-1.169	0.649	-2.268	-0.170	1.000	6714.764	5139.543
H[7]	-0.234	0.588	-1.195	0.672	1.002	5076.004	5060.476
H[8]	1.213	0.570	0.355	2.218	1.001	4389.700	5537.353
H[9]	0.823	0.824	-0.577	2.108	1.001	5338.110	4003.320
D[1]	0.461	0.253	0.097	0.932	1.000	2983.543	2565.263
D[2]	0.925	0.350	0.359	1.529	1.001	2810.568	3022.820
D[3]	0.251	0.186	0.022	0.613	1.001	3483.762	2882.873
D[4]	0.446	0.198	0.169	0.804	1.000	3765.231	3179.683
D[5]	0.450	0.151	0.243	0.725	1.000	5896.061	5536.056
D[6]	0.342	0.167	0.104	0.641	1.001	3743.613	2423.599
D[7]	0.573	0.411	0.044	1.324	1.000	1909.202	3066.287
D[8]	0.621	0.245	0.285	1.069	1.001	3828.092	4701.569
D[9]	0.196	0.143	0.016	0.463	1.000	3181.170	2733.067
sigma	0.824	0.050	0.745	0.909	1.001	5443.715	5411.834

Y vemos efectivamente que el uso de la escala de los jueces es considerablemente diferente, y que hemos absorbido parte de la variación con los parámetros \(H\) y \(D\) (\(sigma\) es más baja que en los modelos anteriores):

mcmc_intervals(ajuste_vinos_3$draws(c("H", "D", "sigma")))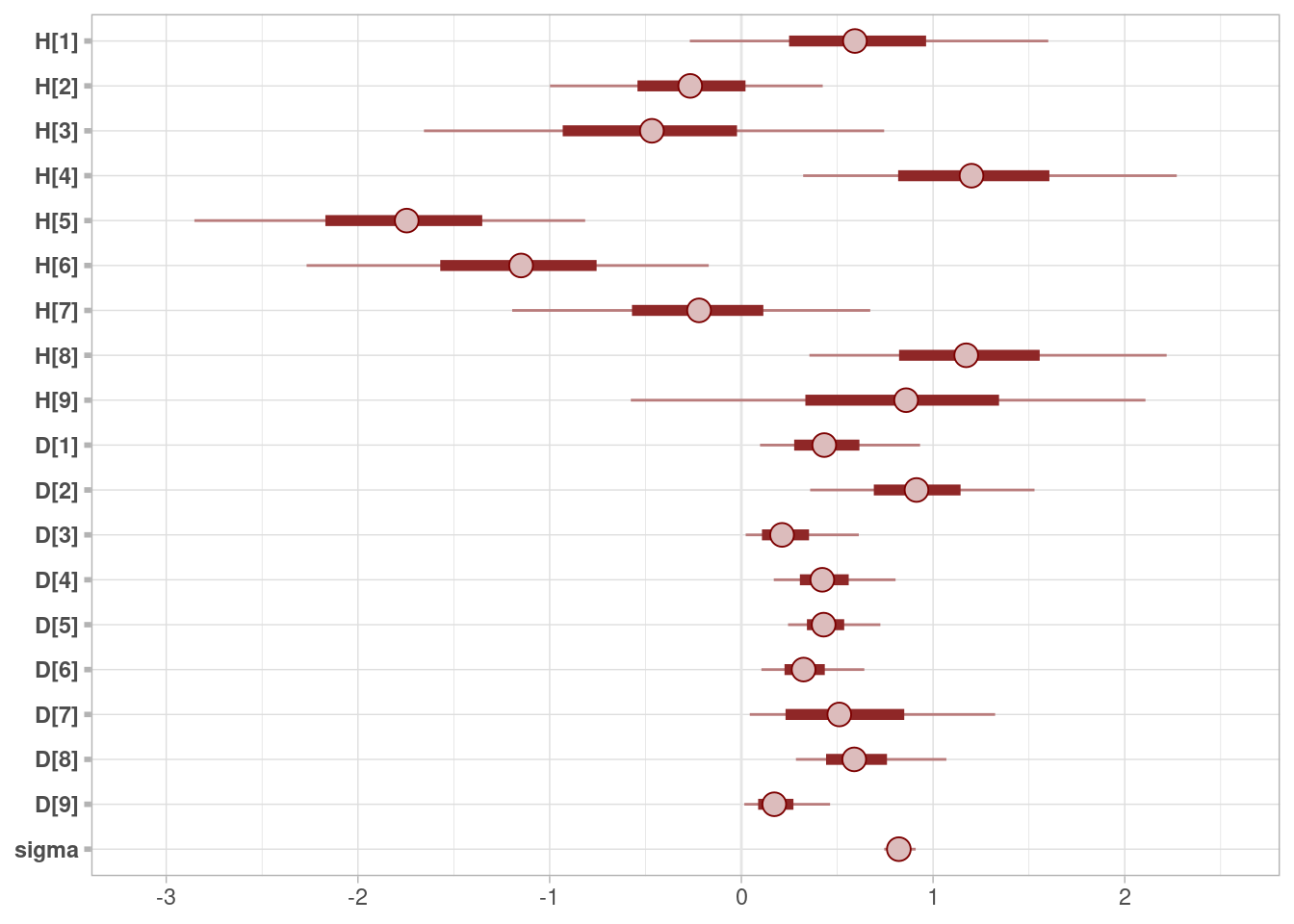

mcmc_intervals(ajuste_vinos_3$draws(c("Q")))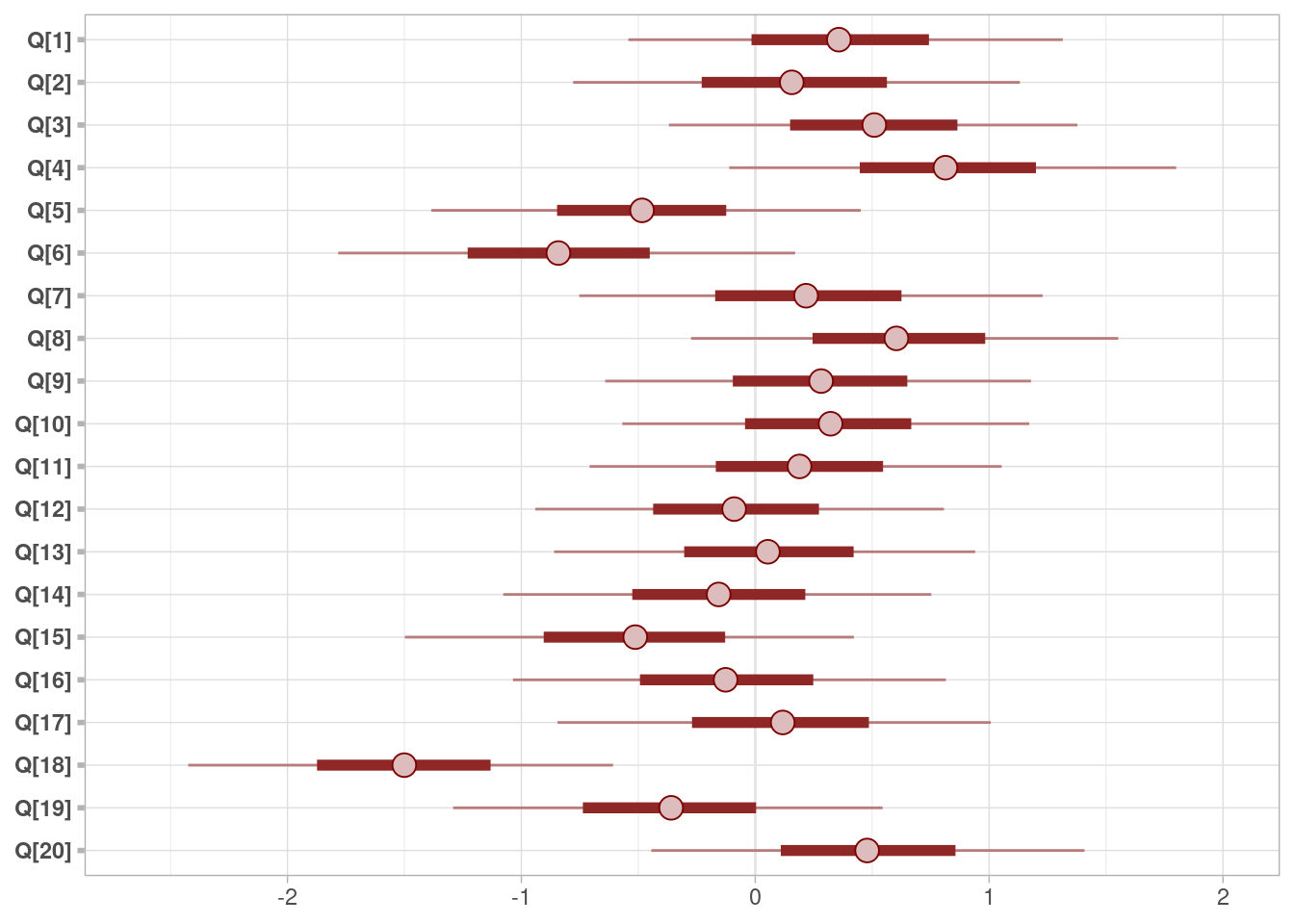

mcmc_intervals(ajuste_vinos_1$draws(c("Q")))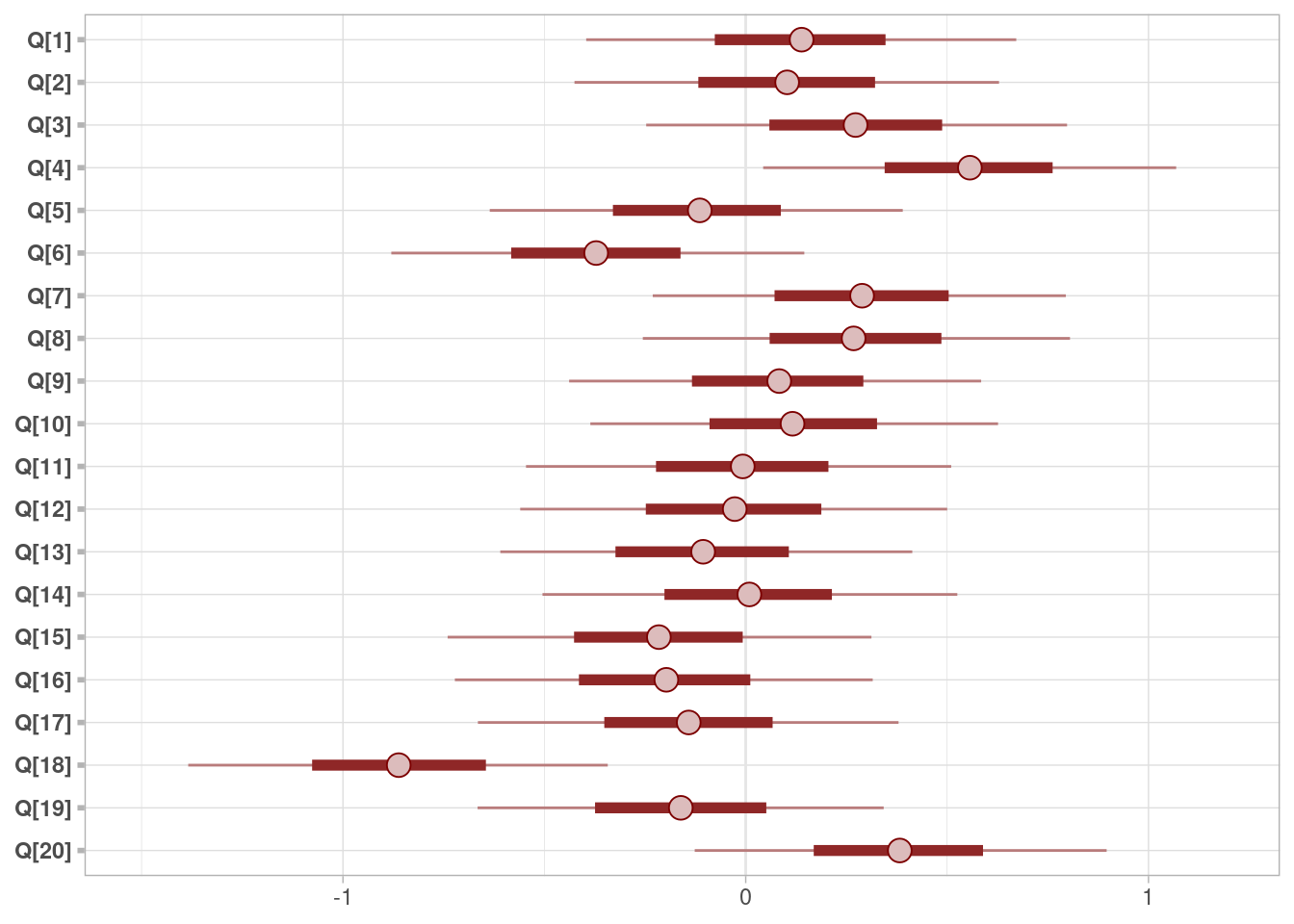

Con el modelo completo, examinamos ahora el contraste de interés: ¿hay diferencias en las calificaciones de vinos de diferentes orígenes? La respuesta es que no hay mucha evidencia de que haya una diferencia, aunque hay variación considerable en este contraste:

ajuste_vinos_3$summary(c("dif_origen")) |> 
  select(variable, mean, sd, q5, q95, rhat, contains("ess")) |> 
  mutate(across(c(mean, sd, q5, q95, rhat, ess_bulk, ess_tail), ~round(., 3))) 

# A tibble: 1 × 8
  variable     mean    sd    q5   q95  rhat ess_bulk ess_tail
  <chr>       <dbl> <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl>
1 dif_origen -0.312 0.497 -1.12 0.495  1.00    4087.    4952.

mcmc_hist(ajuste_vinos_3$draws("dif_origen"), binwidth = 0.07)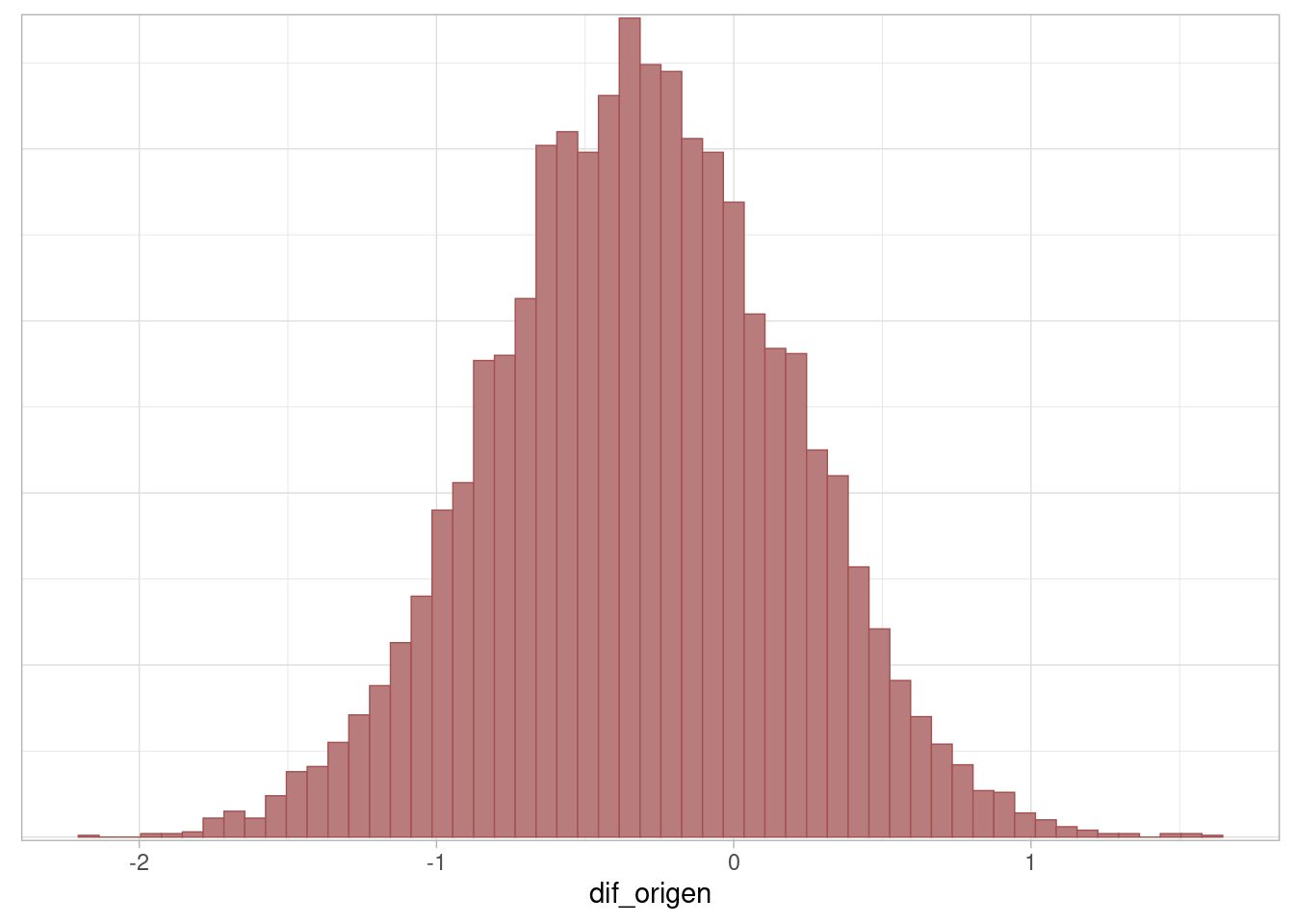

8.5 Transiciones divergentes

Finalmente, discutiremos otro tipo de diagnósticos de Stan. Cuando una trayectoria tuvo un cambio grande en energía \(H\) desde su valor actual a la propuesta final, usualmente del orden de 10^3 por ejemplo, esto implica un rechazo “fuerte” en el nuevo punto de la trayectoria, e implica que la el integrador numérico falló de manera grave.

Transiciones divergentes

Cuando en Stan obtenemos un número considerable de transiciones divergentes, generalmente esto indica que el integrador numérico de Stan no está funcionando bien, y por lo tanto la exploración puede ser deficiente y/o puede estar sesgada al espacio de parámetros donde no ocurren estos rechazos.

Esto puede pasar cuando encontramos zonas de alta curvatura en el espacio de parámetros. Que una posterior esté altamente concentrada o más dispersa generalmente no es un problema, pero si la concentración varía fuertemente (curvatura) entonces puede ser difícil encontrar la escala correcta para que el integrador funcione apropiadamente.

8.5.1 El embudo de Neal

Para ver un ejemplo, consideremos un ejemplo de una distribución cuya forma aparecerá más tarde en modelos jerárquicos. Primero, la marginal de \(y\) es normal con media 0 y desviación estándar 3. La distribución condicional \(p(x|y)\) de \(x = c(x_1,\ldots, x_9)\) dado \(y\) es normal multivariada, todas con media cero y desviación estándar \(e^{y/2}\). Veamos qué pasa si intentamos simular de esta distribución en Stan:

mod_embudo <- cmdstan_model("./src/embudo-neal.stan")
ajuste_embudo <- mod_embudo$sample(
  chains = 1,
  iter_warmup = 1000,
  iter_sampling = 3000,
  refresh = 1000)

Running MCMC with 1 chain...

Chain 1 Iteration:    1 / 4000 [  0%]  (Warmup) 
Chain 1 Iteration: 1000 / 4000 [ 25%]  (Warmup) 
Chain 1 Iteration: 1001 / 4000 [ 25%]  (Sampling) 
Chain 1 Iteration: 2000 / 4000 [ 50%]  (Sampling) 
Chain 1 Iteration: 3000 / 4000 [ 75%]  (Sampling) 
Chain 1 Iteration: 4000 / 4000 [100%]  (Sampling) 
Chain 1 finished in 0.1 seconds.

Warning: 86 of 3000 (3.0%) transitions ended with a divergence.
See https://mc-stan.org/misc/warnings for details.

Warning: 1 of 1 chains had an E-BFMI less than 0.3.
See https://mc-stan.org/misc/warnings for details.

Y vemos que aparecen algunos problemas.

simulaciones <- ajuste_embudo$draws(format = "df")
diagnosticos <- ajuste_embudo$sampler_diagnostics(format = "df")
sims_diag <- simulaciones |> inner_join(diagnosticos, by = c(".draw", ".iteration", ".chain"))
ajuste_embudo$summary() |> 
  select(variable, mean, rhat, contains("ess")) 

# A tibble: 11 × 5
   variable    mean  rhat ess_bulk ess_tail
   <chr>      <dbl> <dbl>    <dbl>    <dbl>
 1 lp__     -5.55    1.35     2.45    NA   
 2 y         0.189   1.34     2.46     2.23
 3 x[1]      0.208   1.28  2494.     417.  
 4 x[2]     -0.0835  1.25  1208.     346.  
 5 x[3]     -0.0653  1.18   294.     300.  
 6 x[4]     -0.0787  1.28  1015.     288.  
 7 x[5]     -0.0731  1.28  1912.     251.  
 8 x[6]      0.0298  1.34  2737.     266.  
 9 x[7]      0.0539  1.17   452.     248.  
10 x[8]     -0.0301  1.30  2469.     313.  
11 x[9]      0.0600  1.23  1814.     348.  

ggplot(sims_diag, aes(y = y, x = `x[1]`)) +
  geom_point(alpha = 0.1) +
  geom_point(data = sims_diag |> filter(divergent__ == 1), color = "red", size = 2) +
  geom_hline(yintercept = -2.5, linetype = 2)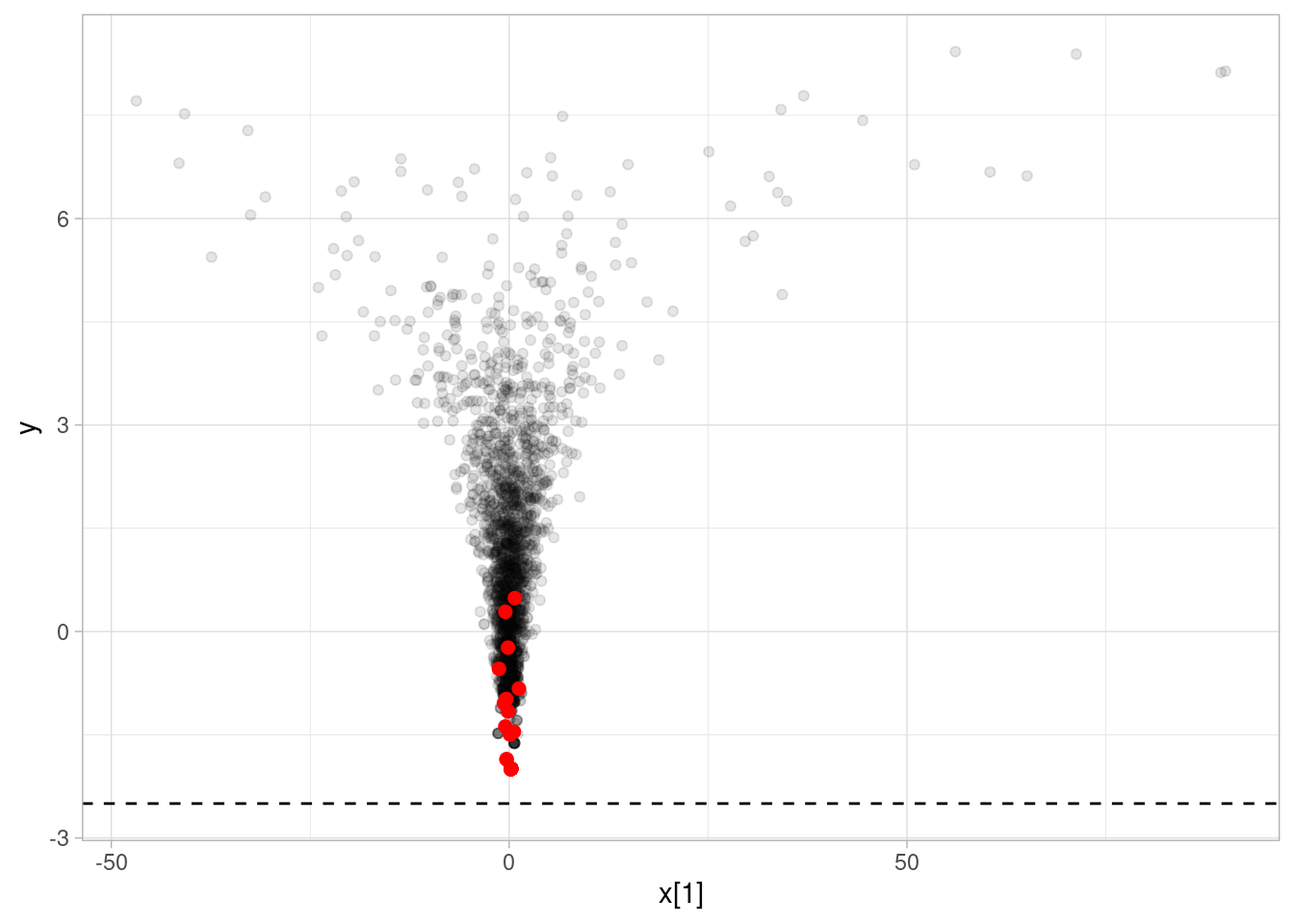 

Y vemos que hay transiciones divergentes. Cuando el muestreador entra en el cuello del embudo, es muy fácil que se “despeñe” en probabilidad y que no pueda explorar correctamente la forma del cuello. Esto lo podemos ver, por ejemplo, si hacemos más simulaciones:

mod_embudo <- cmdstan_model("./src/embudo-neal.stan")
print(mod_embudo)

parameters {
  real y;
  vector[9] x;
}
model {
  y ~ normal(0, 3);
  x ~ normal(0, exp(y/2));
}

ajuste_embudo <- mod_embudo$sample(
  chains = 1,
  iter_warmup = 1000,
  iter_sampling = 30000,
  refresh = 10000)

Running MCMC with 1 chain...

Chain 1 Iteration:     1 / 31000 [  0%]  (Warmup) 
Chain 1 Iteration:  1001 / 31000 [  3%]  (Sampling) 
Chain 1 Iteration: 11000 / 31000 [ 35%]  (Sampling) 
Chain 1 Iteration: 21000 / 31000 [ 67%]  (Sampling) 
Chain 1 Iteration: 31000 / 31000 [100%]  (Sampling) 
Chain 1 finished in 0.8 seconds.

Warning: 1200 of 30000 (4.0%) transitions ended with a divergence.
See https://mc-stan.org/misc/warnings for details.

Warning: 16 of 30000 (0.0%) transitions hit the maximum treedepth limit of 10.
See https://mc-stan.org/misc/warnings for details.

Warning: 1 of 1 chains had an E-BFMI less than 0.3.
See https://mc-stan.org/misc/warnings for details.

ajuste_embudo$summary() |> 
  select(variable, mean, rhat, contains("ess")) 

# A tibble: 11 × 5
   variable      mean  rhat ess_bulk ess_tail
   <chr>        <dbl> <dbl>    <dbl>    <dbl>
 1 lp__     -14.2      1.01     55.4     13.7
 2 y          2.08     1.01     57.6     27.2
 3 x[1]       0.227    1.00  13728.    2727. 
 4 x[2]       0.175    1.00  10467.    2770. 
 5 x[3]      -0.0281   1.01   6702.    2551. 
 6 x[4]      -0.112    1.01   7941.    2514. 
 7 x[5]      -0.0890   1.01   6287.    2346. 
 8 x[6]       0.0658   1.00  10519.    2765. 
 9 x[7]      -0.121    1.00  12467.    2538. 
10 x[8]      -0.107    1.00   7124.    2443. 
11 x[9]       0.00905  1.00   2954.    2351. 

simulaciones <- ajuste_embudo$draws(format = "df")
diagnosticos <- ajuste_embudo$sampler_diagnostics(format = "df")
sims_diag <- simulaciones |> inner_join(diagnosticos, by = c(".draw", ".iteration", ".chain"))
ggplot(sims_diag, aes(y = y, x = `x[1]`)) +
  geom_point(alpha = 0.1) +
  geom_point(data = sims_diag |> filter(divergent__ == 1), color = "red", size = 2) +
  geom_hline(yintercept = -2.5, linetype = 2)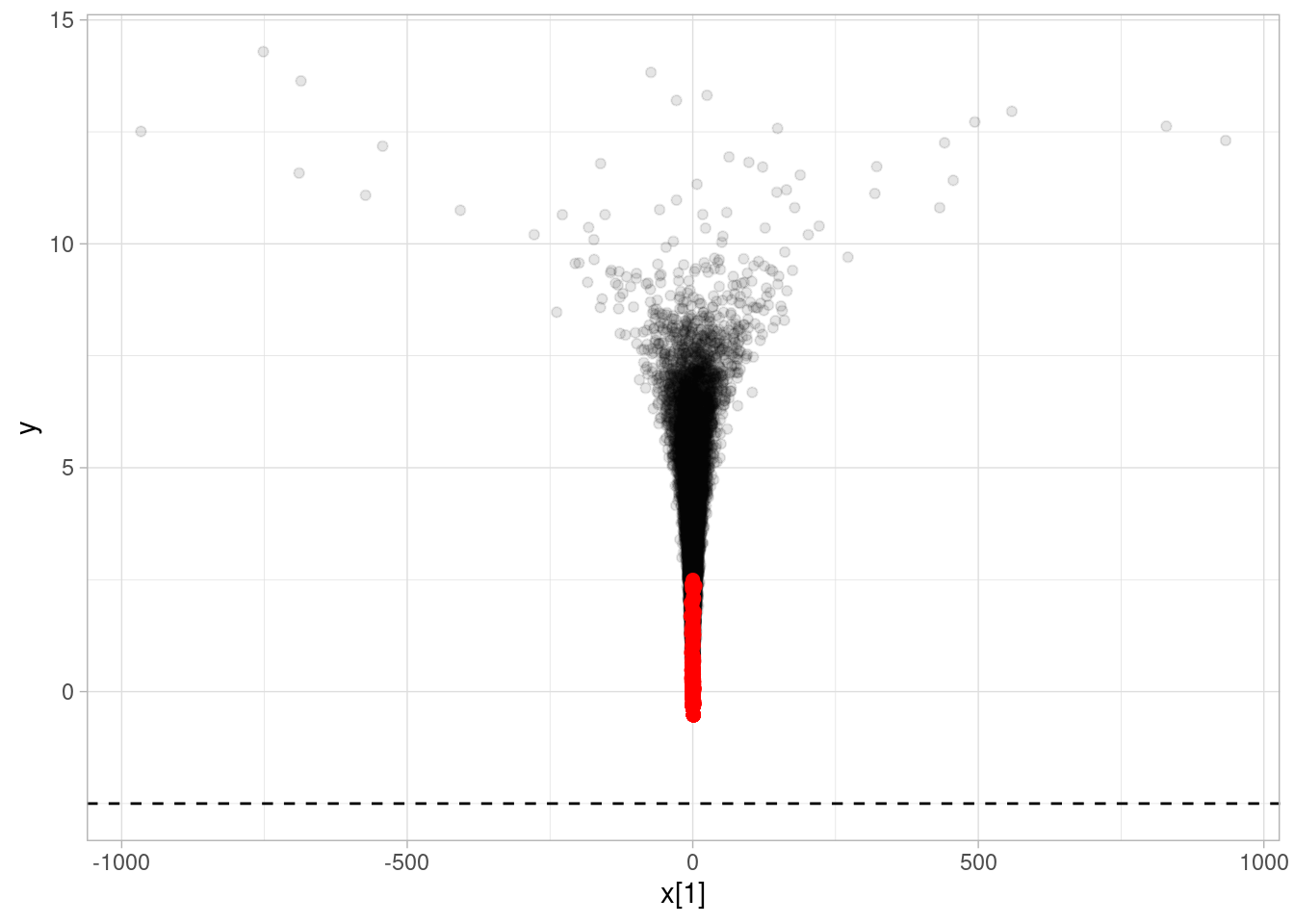 

Y vemos que ahora que en el primer ejemplo estábamos probablemente sobreestimando la media de \(y\). Las divergencias indican que esto puede estar ocurriendo. En este ejemplo particular, también vemos que las R-hat y los tamaños efectivos de muestra son bajos.

Este es un ejemplo extremo. Sin embargo, podemos reparametrizar para hacer las cosas más fáciles para el muestreador. Podemos simular \(y\), y después, simular \(x\) como \(x \sim e^{y/2} z\) donde \(z\) es normal estándar.

mod_embudo_reparam <- cmdstan_model("./src/embudo-neal-reparam.stan")
print(mod_embudo_reparam)

parameters {
  real y;
  vector[9] z;
}

transformed parameters {
  vector[9] x;

  x = exp(y/2) * z;

}

model {
  y ~ normal(0, 3);
  z ~ std_normal();
}

ajuste_embudo <- mod_embudo_reparam$sample(
  chains = 4,
  iter_warmup = 1000,
  iter_sampling = 10000,
  refresh = 1000)

Running MCMC with 4 sequential chains...

Chain 1 Iteration:     1 / 11000 [  0%]  (Warmup) 
Chain 1 Iteration:  1000 / 11000 [  9%]  (Warmup) 
Chain 1 Iteration:  1001 / 11000 [  9%]  (Sampling) 
Chain 1 Iteration:  2000 / 11000 [ 18%]  (Sampling) 
Chain 1 Iteration:  3000 / 11000 [ 27%]  (Sampling) 
Chain 1 Iteration:  4000 / 11000 [ 36%]  (Sampling) 
Chain 1 Iteration:  5000 / 11000 [ 45%]  (Sampling) 
Chain 1 Iteration:  6000 / 11000 [ 54%]  (Sampling) 
Chain 1 Iteration:  7000 / 11000 [ 63%]  (Sampling) 
Chain 1 Iteration:  8000 / 11000 [ 72%]  (Sampling) 
Chain 1 Iteration:  9000 / 11000 [ 81%]  (Sampling) 
Chain 1 Iteration: 10000 / 11000 [ 90%]  (Sampling) 
Chain 1 Iteration: 11000 / 11000 [100%]  (Sampling) 
Chain 1 finished in 0.2 seconds.
Chain 2 Iteration:     1 / 11000 [  0%]  (Warmup) 
Chain 2 Iteration:  1000 / 11000 [  9%]  (Warmup) 
Chain 2 Iteration:  1001 / 11000 [  9%]  (Sampling) 
Chain 2 Iteration:  2000 / 11000 [ 18%]  (Sampling) 
Chain 2 Iteration:  3000 / 11000 [ 27%]  (Sampling) 
Chain 2 Iteration:  4000 / 11000 [ 36%]  (Sampling) 
Chain 2 Iteration:  5000 / 11000 [ 45%]  (Sampling) 
Chain 2 Iteration:  6000 / 11000 [ 54%]  (Sampling) 
Chain 2 Iteration:  7000 / 11000 [ 63%]  (Sampling) 
Chain 2 Iteration:  8000 / 11000 [ 72%]  (Sampling) 
Chain 2 Iteration:  9000 / 11000 [ 81%]  (Sampling) 
Chain 2 Iteration: 10000 / 11000 [ 90%]  (Sampling) 
Chain 2 Iteration: 11000 / 11000 [100%]  (Sampling) 
Chain 2 finished in 0.2 seconds.
Chain 3 Iteration:     1 / 11000 [  0%]  (Warmup) 
Chain 3 Iteration:  1000 / 11000 [  9%]  (Warmup) 
Chain 3 Iteration:  1001 / 11000 [  9%]  (Sampling) 
Chain 3 Iteration:  2000 / 11000 [ 18%]  (Sampling) 
Chain 3 Iteration:  3000 / 11000 [ 27%]  (Sampling) 
Chain 3 Iteration:  4000 / 11000 [ 36%]  (Sampling) 
Chain 3 Iteration:  5000 / 11000 [ 45%]  (Sampling) 
Chain 3 Iteration:  6000 / 11000 [ 54%]  (Sampling) 
Chain 3 Iteration:  7000 / 11000 [ 63%]  (Sampling) 
Chain 3 Iteration:  8000 / 11000 [ 72%]  (Sampling) 
Chain 3 Iteration:  9000 / 11000 [ 81%]  (Sampling) 
Chain 3 Iteration: 10000 / 11000 [ 90%]  (Sampling) 
Chain 3 Iteration: 11000 / 11000 [100%]  (Sampling) 
Chain 3 finished in 0.2 seconds.
Chain 4 Iteration:     1 / 11000 [  0%]  (Warmup) 
Chain 4 Iteration:  1000 / 11000 [  9%]  (Warmup) 
Chain 4 Iteration:  1001 / 11000 [  9%]  (Sampling) 
Chain 4 Iteration:  2000 / 11000 [ 18%]  (Sampling) 
Chain 4 Iteration:  3000 / 11000 [ 27%]  (Sampling) 
Chain 4 Iteration:  4000 / 11000 [ 36%]  (Sampling) 
Chain 4 Iteration:  5000 / 11000 [ 45%]  (Sampling) 
Chain 4 Iteration:  6000 / 11000 [ 54%]  (Sampling) 
Chain 4 Iteration:  7000 / 11000 [ 63%]  (Sampling) 
Chain 4 Iteration:  8000 / 11000 [ 72%]  (Sampling) 
Chain 4 Iteration:  9000 / 11000 [ 81%]  (Sampling) 
Chain 4 Iteration: 10000 / 11000 [ 90%]  (Sampling) 
Chain 4 Iteration: 11000 / 11000 [100%]  (Sampling) 
Chain 4 finished in 0.2 seconds.

All 4 chains finished successfully.
Mean chain execution time: 0.2 seconds.
Total execution time: 1.0 seconds.

Y con este truco de reparametrización el muestreador funciona correctamente (observa que la media de \(y\) está estimada correctamente, y no hay divergencias).

ajuste_embudo$summary() |> 
  select(variable, mean, rhat, contains("ess")) |> 
  mutate(across(c(mean, rhat, ess_bulk, ess_tail), ~round(., 3))) 

# A tibble: 20 × 5
   variable   mean  rhat ess_bulk ess_tail
   <chr>     <dbl> <dbl>    <dbl>    <dbl>
 1 lp__     -5.00      1   16285.   24865.
 2 y         0.002     1   74705.   28688.
 3 z[1]     -0.001     1   85160.   29570.
 4 z[2]     -0.002     1   84329.   30159.
 5 z[3]     -0.006     1   83548.   29967.
 6 z[4]      0.002     1   81672.   29573.
 7 z[5]      0         1   81966.   31008.
 8 z[6]     -0.004     1   85319.   29486.
 9 z[7]      0.001     1   85417.   28666.
10 z[8]      0         1   83917.   28876.
11 z[9]      0.004     1   83128.   30034.
12 x[1]     -0.022     1   41969.   31013.
13 x[2]     -0.036     1   39866.   29902.
14 x[3]     -0.133     1   40322.   30635.
15 x[4]      0.023     1   41022.   29315.
16 x[5]     -0.008     1   41923.   31293.
17 x[6]     -0.116     1   41851.   29370.
18 x[7]      0.005     1   42307.   30895.
19 x[8]     -0.043     1   40895.   29853.
20 x[9]     -0.021     1   39208.   28808.

Brooks, Steve, Andrew Gelman, Galin Jones, y Xiao-Li Meng. 2011. Handbook of Markov Chain Monte Carlo. CRC press.

McElreath, R. 2020. Statistical Rethinking: A Bayesian Course with Examples in R and Stan. A Chapman & Hall libro. CRC Press. https://books.google.com.mx/books?id=Ie2vxQEACAAJ.