8 Clasificación y probabilidad

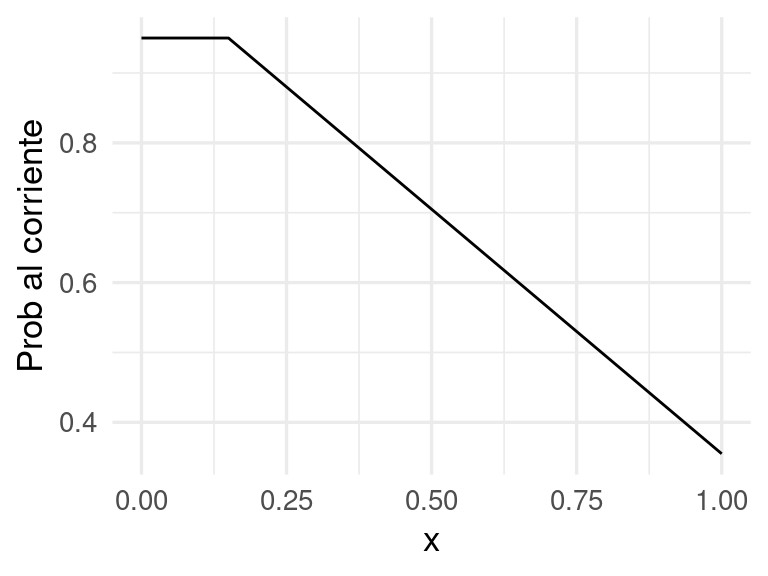
Una variable $g$ categórica o cualitativa toma valores que no son numéricos. Por ejemplo, si $g$ denota el estado del contrato de celular de un cliente dentro de un año, podríamos tener $g\in \{ activo, cancelado\}$.

En un problema de clasificación buscamos predecir una variable respuesta categórica $g$ en función de otras variables de entrada $x=(x_1,x_2,\ldots, x_p)$.

Ejemplos

Predecir si un cliente cae en impago de una tarjeta de crédito, de forma que podemos tener $g=corriente$ o $g=impago$. Variables de entrada podrían ser $x_1=$ porcentaje de saldo usado, $x_2=$ atrasos en los últimos 3 meses, $x_3=$ edad, etc
En reconocimiento de imágenes quiza tenemos que $g$ pertenece a un conjunto que típicamente contiene hasta cientos de valores (manzana, árbol, pluma, perro, coche, persona, cara, etc.). Las $x_j$ son valores de pixeles de la imagen para tres canales (rojo, verde y azul). Si las imágenes son de 100x100, tendríamos 30,000 variables de entrada.

8.1 ¿Qué estimar en problemas de clasificación?

Cuando clasificamos según entradas $x$ en una clase, podemos estar más o menos seguros de la clasificación. Por ejemplo: puede ser que la la decisión es clasificar a un cliente dado como “impago en los próximos tres meses”. La incertidumbe está en que quizá la probabilidad de impago es de 95%, pero existe una probabilidad de 5% de que el cliente se mantenga al corriente. Esto es muy diferente a un cliente con probabilidades respectivas de 60% y 40%. En general, cualquier tipo de análisis costo-beneficio que utilice el modelo debe intentar tomar en cuenta que estos dos clientes son muy diferentes.

Consideramos primero un problema de clasificación binaria, y denotamos por $y\in \{0,1\}$ la indicadora de una de las dos de las categorías. Sea $p(x)$ una función que mide qué tan seguros estamos que la observación es de clase $y=1$. Supondremos que $p(x)$ es una función que toma valores entre $0$ y $1$.

Ahora necesitamos una función de pérdida $L(y, p)$ que evalúa el error cuando nuestra medida de confianza es $p$ y la clase observada es $y$. Podemos usar por ejemplo la pérdida cuadrática:

\[L(y, p) = (y - p)^2,\] que también se llama pérdida de Brier en este contexto. Igual que en regresión, dada una población, podemos encontrar la función $p^*(x)$ que minimiza la pérdida esperada sobre toda la población. En este caso, \[p^*(x) = E(y|x) = P(y=1|x)\] es decir, la verdadera probabilidad de que la clase sea 1 es la función $p^*(x)$ que minimiza la pérdida cuadrática. Si usamos por ejemplo la pérdida absoluta, entonces la solucion es tomar como $p^* (x) = 1$ si $P(y= 1|x) > 0.5$, y $p^*(x)= 0$ en otro caso (muestra por qué).

Aunque utilizaremos otras pérdidas mejor adaptadas para el problema del clasificación, por el momento notemos que igual que planteamos el problema aprendizaje en regresión como un problema de aproximar una curva $f^*(x)$ óptima con una función $\hat{f}(x)$ construida a partir de datos, igualmente podemos plantear el problema de clasificación binaria como sigue:

Buscamos algoritmos ${\mathcal L} \to \hat{p}(x)$ tal que $\hat{p}(x)$ está cercana a la probabilidad de clase $p^* (x) = P(y=1 |x)$.
Los argumentos de error irreducible, sesgo y variabilidad aplican también en esta situación bajo la pérdida de Brier y puede darse un argumento para cada clase (considerando $y_k - \hat{p}_k(x)$ como residual). En este caso, el error irreducible proviene del hecho de que $p^*_k(x)$ no necesariamente toman solo los valores 0 o 1, y dadas las $x$, existe incertidumbre en la clase que vamos a observar.

Ejemplo

(Impago de tarjetas de crédito) Supongamos que $x=$ porcentaje del crédito máximo usado, y $y\in\{0, 1\}$, donde $1$ corresponde al corriente y $0$ representa impago. Las probabilidades condicionales de clase para la clase al corriente podrían ser, por ejemplo:

$p(x) = P(y=1|x) =0.95$ si $x < 0.15$
$p(x) = P(y=1|x) = 0.95 - 0.7(x - 0.15)$ si $x>=0.15$

Estas son probabilidades y no determinan el resultado, pues hay otras variables que influyen en que un cliente permanezca al corriente o no en sus pagos más allá de información contenida en el porcentaje de crédito usado. Nótese que estas probabilidades son diferentes a las no condicionadas, por ejempo, podríamos tener que a total $P(y=1)=0.83$

library(tidyverse)
library(tidymodels)
library(gt)
p_1 <- function(x){
  ifelse(x < 0.15, 0.95, 0.95 - 0.7 * (x - 0.15))
}
ggplot(tibble(x = seq(0, 1, 0.01)), aes(x = x)) + 
    stat_function(fun = p_1)  +
    ylab("Prob al corriente")

8.2 Estimación de probabilidades de clase

¿Cómo estimamos ahora las probabilidades de clase a partir de una muestra de entrenamiento? Veremos por ahora dos métodos: k-vecinos más cercanos y regresión logística.

Ejemplo

Vamos a generar unos datos con el modelo simple del ejemplo anterior:

simular_impago <- function(n = 500){
    # suponemos que los valores de x están concentrados en valores bajos,
    # quizá la manera en que los créditos son otorgados
    clases <- c("al_corriente", "impago")
    x <- pmin(rexp(n, 100 / 40), 1)
    # las probabilidades de estar al corriente:
    prob <- p_1(x)
    # finalmente, simulamos cuáles clientes siguen al corriente y cuales no:
    g <- map_chr(1:length(x), ~ sample(clases, size = 1, prob = c(prob[.x], 1- prob[.x])))
    g <- factor(g, levels = c("al_corriente", "impago"))
    datos <- tibble(x = x, p_1 = prob, g = g) |> 
      mutate(y = ifelse(g == "al_corriente", 1, 0))
    datos
}
set.seed(193)
dat_ent  <- simular_impago() |> select(x, g, y) 
dat_ent |> sample_n(20)

# A tibble: 20 × 3
         x g                y
     <dbl> <fct>        <dbl>
 1 0.118   al_corriente     1
 2 0.109   al_corriente     1
 3 0.444   al_corriente     1
 4 0.153   al_corriente     1
 5 0.100   al_corriente     1
 6 0.0109  al_corriente     1
 7 0.216   al_corriente     1
 8 1       impago           0
 9 0.0846  al_corriente     1
10 0.144   al_corriente     1
11 0.377   impago           0
12 0.0908  al_corriente     1
13 0.128   al_corriente     1
14 0.00262 al_corriente     1
15 0.411   al_corriente     1
16 0.545   al_corriente     1
17 0.402   al_corriente     1
18 0.0544  al_corriente     1
19 0.00265 al_corriente     1
20 0.0927  al_corriente     1

Como este problema es de dos clases, podemos graficar como sigue (agregamos variación artificial en $y$ para evitar traslape de los puntos):

graf_1 <- ggplot(dat_ent, aes(x = x)) +
  geom_jitter(aes(colour = factor(g), y = y), 
    width=0.02, height=0.1) + ylab("") + 
    labs(colour = "Clase")
graf_1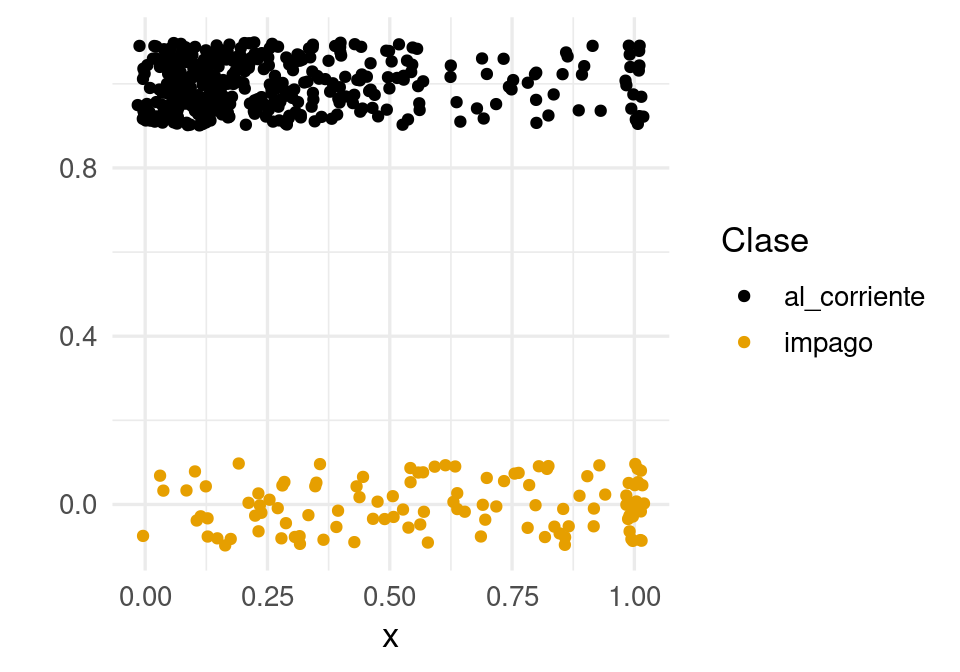

8.3 k-vecinos más cercanos

Para usar $k$-vecinos más cercanos para estimar la probabilidades de clase para cada $x$, podemos tomar una vecindad de la $x$ donde queremos predecir, y tomar el siguiente promedio:

\[\hat{p}(x) = \frac{1}{k}\sum_{x^{(i)} \in N_k(x)} y^{(i)},\]

que es la proporción de unos en una vecindad $N_k(x)$ de $x$.

Ejemplo

Vamos a intentar estimar la probabilidad condicional de estar al corriente usando k vecinos más cercanos:

vmc_modelo <- nearest_neighbor(neighbors = 100, weight_func = "gaussian") |> 
  set_engine("kknn") |> 
  set_mode("classification")
ajuste_vmc <- vmc_modelo |> fit(g ~ x, dat_ent)
# para graficar:
graf_kvmc <- tibble(x = seq(0, 1, 0.01))
graf_kvmc <- predict(ajuste_vmc, graf_kvmc, type = "prob") |> 
  bind_cols(graf_kvmc) |> 
  select(x, .pred_al_corriente)
graf_kvmc |> head()

# A tibble: 6 × 2
      x .pred_al_corriente
  <dbl>              <dbl>
1  0                 0.947
2  0.01              0.946
3  0.02              0.948
4  0.03              0.954
5  0.04              0.973
6  0.05              0.985

Y la curva roja da nuestra estimación de probabilidad de impago para cada $x4:

graf_verdadero <- tibble(x = seq(0, 1, 0.01), p_1 = p_1(x))
graf_2 <- graf_1 + 
  geom_line(data = graf_kvmc, aes(y = .pred_al_corriente), colour = 'red', size=1.2) +
  geom_line(data = graf_verdadero, aes(y = p_1)) +
  ylab('Prob al corriente') + xlab('% crédito usado')

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.

graf_2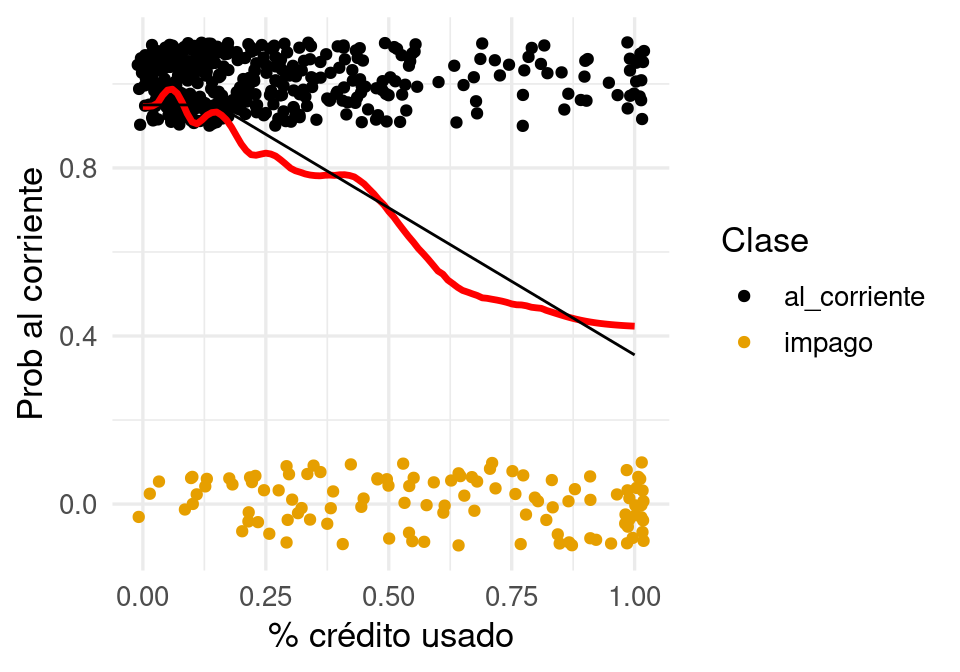

Ahora podríamos usar una muestra de prueba para evaluar nuestra estimación, pues no tenemos la curva negra óptima para comparar.

8.4 Ejemplo: diabetes

Consideremos datos de diabetes en mujeres Pima:

A population of women who were at least 21 years old, of Pima Indian heritage and living near Phoenix, Arizona, was tested for diabetes according to World Health Organization criteria. The data were collected by the US National Institute of Diabetes and Digestive and Kidney Diseases. We used the 532 complete records after dropping the (mainly missing) data on serum insulin.

npreg number of pregnancies.
glu plasma glucose concentration in an oral glucose tolerance test.
bp diastolic blood pressure (mm Hg).
skin triceps skin fold thickness (mm).
bmi body mass index (weight in kg/(height in m)^2).
ped diabetes pedigree function.
age age in years.
type Yes or No, for diabetic according to WHO criteria.

diabetes_ent <- as_tibble(MASS::Pima.tr)
diabetes_pr <- as_tibble(MASS::Pima.te)
diabetes_ent

# A tibble: 200 × 8
   npreg   glu    bp  skin   bmi   ped   age type 
   <int> <int> <int> <int> <dbl> <dbl> <int> <fct>
 1     5    86    68    28  30.2 0.364    24 No   
 2     7   195    70    33  25.1 0.163    55 Yes  
 3     5    77    82    41  35.8 0.156    35 No   
 4     0   165    76    43  47.9 0.259    26 No   
 5     0   107    60    25  26.4 0.133    23 No   
 6     5    97    76    27  35.6 0.378    52 Yes  
 7     3    83    58    31  34.3 0.336    25 No   
 8     1   193    50    16  25.9 0.655    24 No   
 9     3   142    80    15  32.4 0.2      63 No   
10     2   128    78    37  43.3 1.22     31 Yes  
# ℹ 190 more rows

Intentaremos predecir diabetes dependiendo del una medición de glucosa en la sangre:

ggplot(diabetes_ent, aes(x = glu, y= ifelse(type=='Yes', 1, 0), colour = type)) +
  geom_jitter(height = 0.05)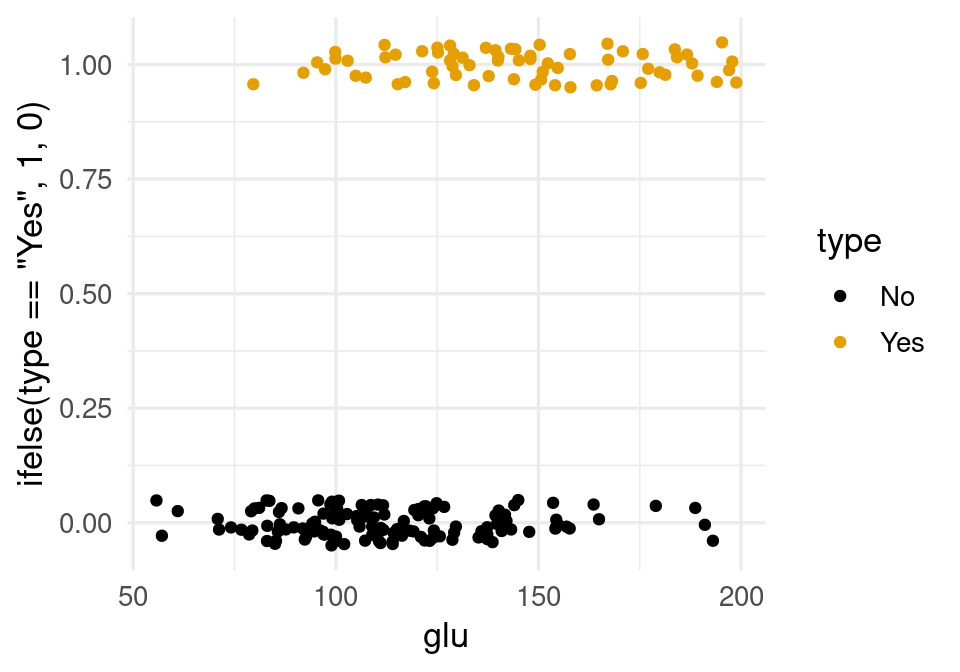

Usamos $30$ vecinos más cercanos para estimar $p(x)$:

graf_data <- tibble(glu = seq(50, 200, 1))
# ajustar modelo
ajuste_vmc_diabetes <- vmc_modelo |> set_args(neighbors = 50) |> 
  fit(type ~ glu, diabetes_ent)
# graficar
graf_data <- predict(ajuste_vmc_diabetes, graf_data, type = "prob") |> 
  bind_cols(graf_data) |> 
  select(glu, .pred_Yes)
ggplot(diabetes_ent, aes(x = glu)) + 
  geom_point(aes(y = as.numeric(type == "Yes"), colour = type)) + 
  geom_line(data = graf_data, aes(y = .pred_Yes)) +
  ylab('Probabilidad diabetes')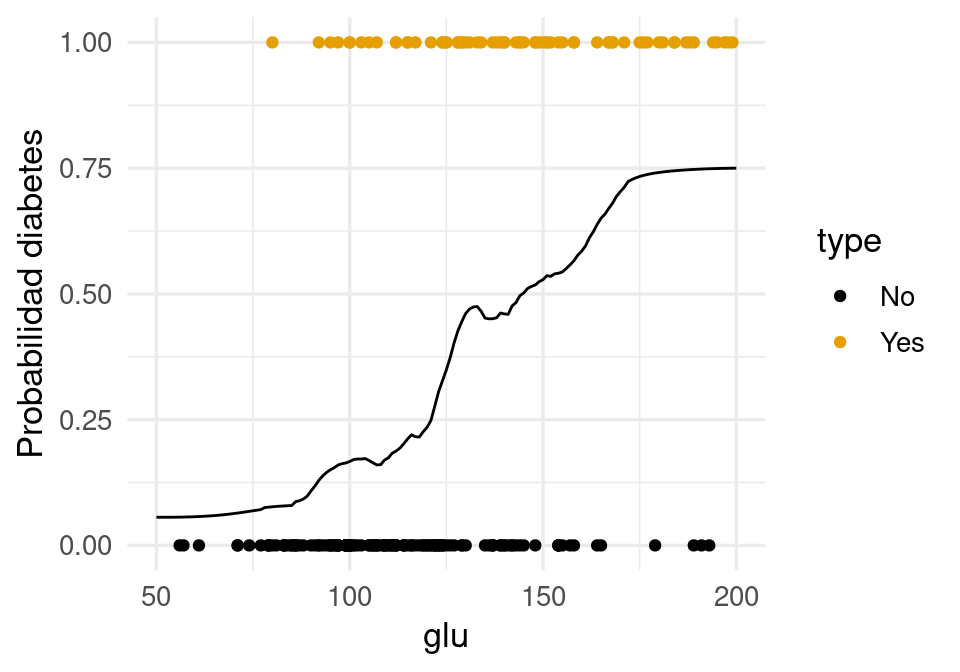

Finalmente, evaluamos por ejemplo con la pérdida de Brier:

preds_tbl <- predict(ajuste_vmc_diabetes, diabetes_pr, type = "prob") |> 
  bind_cols(diabetes_pr |> select(type)) |> 
  mutate(y = as.numeric(type == "Yes")) 
preds_tbl |> head()

# A tibble: 6 × 4
  .pred_No .pred_Yes type      y
     <dbl>     <dbl> <fct> <dbl>
1    0.482    0.518  Yes       1
2    0.921    0.0793 No        0
3    0.902    0.0980 No        0
4    0.925    0.0752 Yes       1
5    0.250    0.750  Yes       1
6    0.342    0.658  Yes       1

preds_tbl |> 
  rmse(truth = y, estimate = .pred_Yes)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard       0.405

Podemos comparar este error con la predicción que haríamos usando la proporción de unos en los datos, por ejemplo:

promedio_ent <- diabetes_ent |> mutate(y = type == "Yes") |> 
  pull(y) |> mean()
preds_tbl |> mutate(promedio = promedio_ent) |> 
  rmse(truth = y, estimate = promedio)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard       0.470

Finalmente, probemos usando todas las variables, teniendo cuidado de estandarizar las variables de entranda:

receta_diabetes <- recipe(type ~ ., diabetes_ent) |> 
  step_normalize(all_predictors())
modelo_vmc <- vmc_modelo |> 
  set_args(neighbors = 50) 
flujo_vmc_diabetes <- workflow() |> 
  add_recipe(receta_diabetes) |> 
  add_model(modelo_vmc)
preds_todas <- fit(flujo_vmc_diabetes, diabetes_ent) |> 
  predict(diabetes_pr, type = "prob") |> 
  bind_cols(diabetes_pr |> select(type)) |> 
  mutate(y = as.numeric(type == "Yes")) 
preds_todas |> 
  rmse(truth = y, estimate = .pred_Yes)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard       0.396

8.5 Pérdida logarítmica

La pérdida de Brier es una medida útil para evaluar modelos, pero tiene algunos defectos cuando se usa en el ajuste de probabilidades de clase. Uno importante es que es penaliza relativamente poco a errores donde predecimos por ejemplo $\hat{p}_1(x) = 0.0001$, y resulta que observamos $g=1$. La penalización es similar que cuando $\hat{p}_1(x) = 0.01$, pero se puede argumentar que el primero de los errores es considerablemente más grave que el segundo.

Consideremos entonces que tenemos una estimación $\hat{p}_g(x)$ de las probabilidad de clase. Supongamos que observamos ahora $(x, g)$ (la clase verdadera es $g$).

Si $\hat{p}_{g}(x)$ es muy cercana a uno, deberíamos penalizar poco, pues dimos probabilidad alta a la clase $g$ que ocurrió.
Si $\hat{p}_{g}(x)$ es chica, deberíamos penalizar más, pues dimos probabilidad baja a observar la clase $g$.
Si $\hat{p}_{g}(x)$ es muy cercana a cero, y observamos $g$, deberíamos hacer una penalización muy alta (convergiendo a $\infty$, pues no es aceptable que sucedan eventos con probabilidad estimada extremadamente baja).

Quisiéramos encontrar una función $h$ apropiada, de forma que la pérdida al observar $(x, g)$ sea \[s(\hat{p}_{g}(x)),\] y que cumpla con los puntos arriba señalados. Entonces tenemos que

$s$ debe ser una función continua y decreciente en $[0,1]$
Podemos poner $s(1)=0$ (no hay pérdida si ocurre algo con que dijimos tiene probabilidad 1)
$s(p)$ debe ser muy grande is $p$ es muy chica.

Una opción analíticamente conveniente es la pérdida logarítmica: \[s(p) = - \log(p)\]

perdidas_tbl <- tibble(p = seq(0.01, 1, 0.001)) |> 
  mutate(logarítmica = - log(p), brier  = 2 * (1 - p)^2) |> 
  pivot_longer(cols = logarítmica:brier, names_to = "tipo", values_to = "perdida")
ggplot(perdidas_tbl, aes(x = p, y = perdida, colour = tipo)) +
  geom_line(size = 1.1)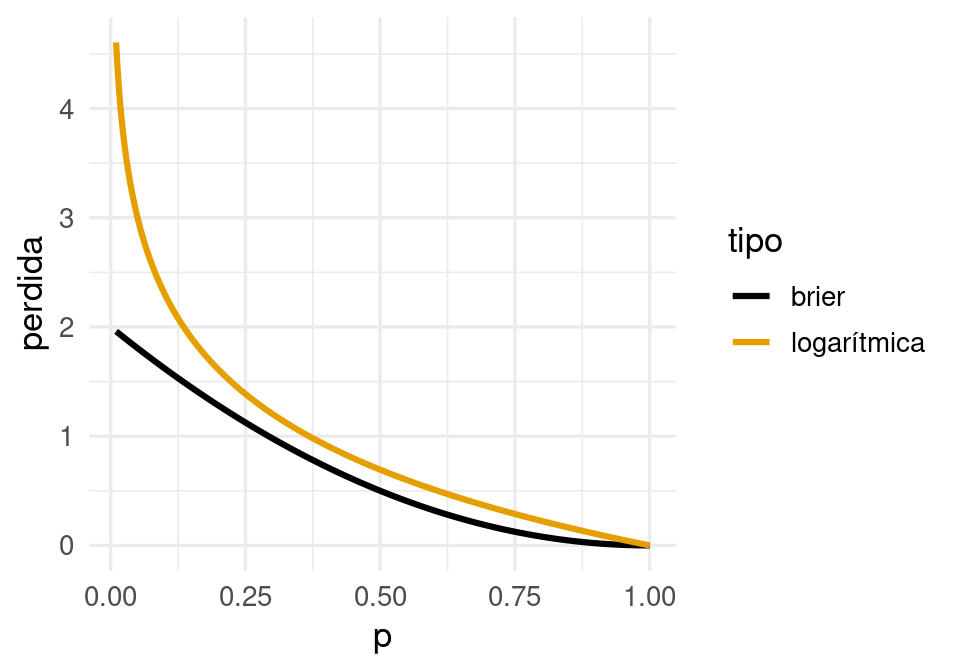

Así que la pérdida para un caso con entradas $x$ y clase $g$ es

\[-\log \hat{p}_g (x)\] Se puede demostrar que, igual que la pérdida de Brier, si queremos minimizar la pérdida logarítmica sobre toda la población, la solución está dada por las verdaderas probabilidades de clase

\[p^*(x) = E(y|x) = P(y = 1|x).\]

De modo que la función que queremos estimar es la misma en ambos casos. La pérdida de Brier sin embargo, es menos sensible a errores en los extremos de la escala de probabilidad, y puede producir estimaciones distintas cuando se usa en entrenamiento.

Observaciones:

La pérdida logarítmica también se llama devianza binomial o devianza multinomial en otros lugares, usualmente multipicada por 2 (lo cual no cambia sus propiedades).
Una razón importante para usar la pérdida logarítmica como el objetivo a minimizar es que equivale a la estimación por máxima verosimilitud (intenta demostrarlo).
No es fácil interpretar la pérdida logarítmica, pero es útil para ajustar y comparar modelos. Veremos otras medidas más fáciles de interpretar más adelante.

Compara la siguiente definición con la que vimos para modelos de regresión:

Pérdida logarítmica

Sea \[{\mathcal L}=\{ (x^{(1)},g^{(1)}),(x^{(2)},g^{(2)}), \ldots, (x^{(N)}, g^{(N)}) \}\] una muestra de entrenamiento, a partir de las cuales construimos mediante un algoritmo funciones estimadas $\hat{p}_{g} (x)$ para $g=1,\ldots, K$. La pérdida logarítmica de entrenamiento está dada por \[\begin{equation} \overline{err} = - \frac{1}{N}\sum_{i=1}^N log(\hat{p}_{g^{(i)}} (x^{(i)})) \end {equation}\] Sea \[{\mathcal T}=\{ (\mathbf{x}^{(1)},\mathbf{g}^{(1)}),(\mathbf{x}^{(2)},\mathbf{g}^{(2)}), \ldots, (\mathbf{x}^{(m)}, \mathbf{g}^{(m)}) \}\] una muestra de prueba. La pérdida logarítmica de prueba es \[\begin{equation} \hat{Err} = - \frac{1}{m}\sum_{i=1}^m log(\hat{p}_{\mathbf{g}^{(i)}} (\mathbf{x}^{(i)})) \end {equation}\] que es una estimación de la devianza de predicción \[-E\left [ \log(\hat{p}_g(x)) \right ],\] donde el promedia se toma sobre todos los valores $(\mathbf{x}, \mathbf{g})$ de la población.

Ejemplo

Regresamos a nuestros ejemplo simulado de impago de tarjetas de crédito. Primero calculamos la pérdida logarítmica de entrenamiento

s <- \(x) -log(x)
dat_log_loss <- ajuste_vmc |>  
  predict(dat_ent, type = "prob") |> 
  bind_cols(dat_ent) |> 
  select(x, g, .pred_impago, .pred_al_corriente)
dat_log_loss <- dat_log_loss |>  
  mutate(hat_p_g = ifelse(g=="impago", .pred_impago, .pred_al_corriente))

Nótese que dependiendo de qué clase observamos (columna $g$), extraemos la probabilidad correspondiente a la columna hat_p_g:

set.seed(125)
dat_log_loss |> sample_n(20) |> gt()

x	g	.pred_impago	.pred_al_corriente	hat_p_g
0.19852287	al_corriente	0.14038901	0.8596110	0.85961099
0.67376004	al_corriente	0.50190033	0.4980997	0.49809967
0.05182251	al_corriente	0.01304586	0.9869541	0.98695414
0.78516363	al_corriente	0.53011453	0.4698855	0.46988547
0.51357278	al_corriente	0.32252677	0.6774732	0.67747323
0.11636840	al_corriente	0.08958375	0.9104162	0.91041625
0.50414410	impago	0.30908738	0.6909126	0.30908738
0.68843401	impago	0.50778339	0.4922166	0.50778339
0.74915741	impago	0.52349703	0.4765030	0.52349703
0.15106073	al_corriente	0.06850996	0.9314900	0.93149004
1.00000000	impago	0.57659107	0.4234089	0.57659107
0.07148778	al_corriente	0.02543890	0.9745611	0.97456110
0.08934583	al_corriente	0.06888669	0.9311133	0.93111331
0.32848650	al_corriente	0.21323646	0.7867635	0.78676354
0.20386137	al_corriente	0.14978783	0.8502122	0.85021217
0.67871350	impago	0.50258385	0.4974162	0.50258385
0.19050443	al_corriente	0.12406591	0.8759341	0.87593409
0.18182276	al_corriente	0.10562898	0.8943710	0.89437102
0.26726265	al_corriente	0.16922039	0.8307796	0.83077961
0.02035980	impago	0.05230648	0.9476935	0.05230648

Ahora aplicamos la función $s$ que describimos arriba, y promediamos sobre el conjunto de entrenamiento:

dat_log_loss <- dat_log_loss |> mutate(dev = s(hat_p_g))
dat_log_loss |> sample_n(20) |> gt()

x	g	.pred_impago	.pred_al_corriente	hat_p_g	dev
0.32253044	al_corriente	0.21043820	0.7895618	0.7895618	0.23627717
0.10851963	al_corriente	0.09528056	0.9047194	0.9047194	0.10013039
0.11801945	al_corriente	0.08830654	0.9116935	0.9116935	0.09245146
1.00000000	impago	0.57659107	0.4234089	0.5765911	0.55062199
0.11771241	al_corriente	0.08871380	0.9112862	0.9112862	0.09289827
0.03576024	al_corriente	0.03671995	0.9632800	0.9632800	0.03741110
0.02947193	al_corriente	0.04638861	0.9536114	0.9536114	0.04749904
0.06708467	al_corriente	0.01865320	0.9813468	0.9813468	0.01882937
0.52670471	al_corriente	0.34240787	0.6575921	0.6575921	0.41917040
0.48074458	impago	0.27713415	0.7228659	0.2771341	1.28325360
0.75320749	impago	0.52403777	0.4759622	0.5240378	0.64619152
0.28789759	al_corriente	0.18845940	0.8115406	0.8115406	0.20882086
0.50724729	al_corriente	0.31267931	0.6873207	0.6873207	0.37495430
0.65972691	impago	0.49530580	0.5046942	0.4953058	0.70257994
1.00000000	al_corriente	0.57659107	0.4234089	0.4234089	0.85941682
0.03525545	al_corriente	0.03771126	0.9622887	0.9622887	0.03844073
0.53221265	impago	0.35093998	0.6490600	0.3509400	1.04714008
0.12557127	al_corriente	0.08047375	0.9195263	0.9195263	0.08389669
0.12686269	al_corriente	0.07830790	0.9216921	0.9216921	0.08154406
0.11702054	al_corriente	0.08882314	0.9111769	0.9111769	0.09301826

dat_log_loss |> ungroup() |> summarise(lloss_entrena = mean(dev))

# A tibble: 1 × 1
  lloss_entrena
          <dbl>
1         0.421

Que también podemos calcular como sigue:

dat_log_loss |> mn_log_loss(g, .pred_al_corriente) |> 
  mutate(.estimate = .estimate )

# A tibble: 1 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 mn_log_loss binary         0.421

Recordemos que la devianza de entrenamiento no es la cantidad que evalúa el desempeño del modelo. Hagamos el cálculo entonces para una muestra de prueba:

set.seed(1213)
dat_prueba <- simular_impago(n = 5000) |> select(x, g)
## calcular para muestra de prueba
dat_log_loss_prueba <- ajuste_vmc |> 
  predict(dat_prueba, type = "prob") |> 
  bind_cols(dat_prueba) |> 
  select(x, g, .pred_impago, .pred_al_corriente)
dat_log_loss_prueba <- dat_log_loss_prueba |> 
  mutate(hat_p_g = ifelse(g == "al_corriente", .pred_al_corriente, .pred_impago))
dat_log_loss_prueba <- dat_log_loss_prueba |> mutate(log_loss = s(hat_p_g))
dat_log_loss_prueba |> ungroup() |> summarise(log_loss_prueba = mean(log_loss))

# A tibble: 1 × 1
  log_loss_prueba
            <dbl>
1           0.434

8.6 Clasificación multinomial

Cuando tenemos sólo dos clases (clasificación binaria), basta con estimar una probabilidad de clase, pues la segunda es complemento de la primera. Para tres o más clases introducimos notación adicional:

Consideramos un problema donde $g$ puede ser una de $K$ clases posibles. Tenemos $K$ probabilidades de clase $p(x) = (p_1(x), p_2(x), \ldots p_K(x))$ que deben sumar 1 (de forma que una de ellas es redundante dadas las otras).
Definimos $(y_1,y_2, \ldots, y_k)$ variables indicadoras de las categorías, donde $y_k = 1$ cuando $g = k$ y $y_k = 0$ en otro caso.

La pérdida de Brier en este caso se puede definir como

\[L(g, p(x)) = \sum_{k=1}^K (y_k - p_k(x))^2 = (1 - p_g(x))^2 + \sum_{k\neq g} (p_k(x))^2\] Esto quiere decir que el score de Brier es chico cuando $p_g(x)$, la probabilidad de la clase $g$, es cercana a uno y el resto de las probabilidades son cercanas a 0 (verifica que esta definición es equivalente para dos clases según la definición mostrada arriba para clasificación binaria). En este caso, la solución teórica que minimiza esta pérdida promediada sobre toda la población es

\[p_k^*(x) = E(y_k | x) = P(g = k| x)\]

Si usamos la pérdida logarítmica, entonces la pérdida es

\[L(g, p(x)) = -\log p_g (x),\] que en nuestra notación con indicadoras se escribe como

\[L(y, p(x)) = -\sum_{k=1}^K y_k\log p_k (x),\]

Ejercicio: escribe las estimaciones de clase de $k$-vecinos más cercanos para clasificación multinomial.

8.7 Regresión logística

En $k$ vecinos más cercanos, intentamos estimar directamente con promedios las probabilidades de clase, sin considerar ninguna estructura. Ahora consideramos modelos más estructurados, definidos por parámetros, e intentaremos ajustarlos minimizando la pérdida logarítmica.

Igual que en regresión lineal, algunos de los modelos más simples que podemos imaginar son modelos lineales. Solo es necesario hacer una adaptación.

Supongamos que nuestra variable respuesta es $y$, que toma valores 0 o 1.

Ahora queremos definir $p(x) = p_1(x)$ (probabilidad de que ocurra la clase 1) en términos de un promedio ponderado de las variables de entrada, como en regresión lineal:

\[\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_px_p.\]

Sin embargo, observamos que esta expresión puede dar valores negativos o mayores a uno, de forma que no necesariamente puede interpetarse como una probabilidad $p(x)$. Una de las formas más sencillas de resolver este problema es transformar esta expresión para que necesariamente esté en $[0,1]$ por medio de una función fija $h$:

\[p_{\beta}(x) = h(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_px_p),\] donde $h$ debe ser una función que mapea valores reales a valores en $[0,1]$.

En este punto hay muchas funciones que podríamos usar. Para simplificar la interpretación y uso de este modelo, podemos escoger entre funciones que satisfagan, por ejemplo:

$h$ toma valores en $[0,1]$ es creciente y diferenciable
$h(0) = 0.5$ (0 equivale a probabilidad 0.5, negativos dan probabilidades menores a 0.5 y positivos dan probabilidades mayores a 0.5)
$h(-x)=1-h(x)$ (simetría). Por ejemplo, si $h(-2)=0.16$ entonces $h(2)= 1-0.16=0.84$.

Hay todavía muchas opciones. Una de las más simples es usar la función logística

Tip

La función logística está dada por \[h(x)=\frac{e^x}{1+e^x}\]

h <- function(x){exp(x)/(1+exp(x)) }
ggplot(tibble(x = seq(-6, 6, 0.01)), aes(x = x)) + stat_function(fun = h)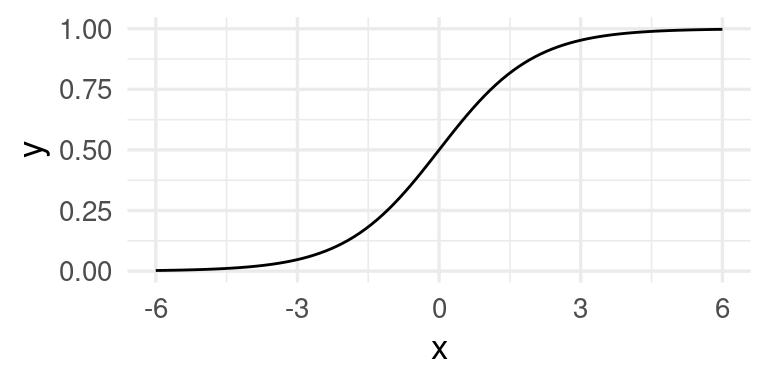

Esta función comprime adecuadamente (para nuestros propósitos) el rango de todos los reales dentro del intervalo $[0,1]$. Si aplicamos al predictor lineal que consideramos, obtenemos:

Regresión logística

El modelo de regresión logística está dado por \[p_1(x)=p_1(x;\beta)= h(\beta_0+\beta_1x_1 + \beta_2 x_2 + \cdots + \beta_p x_p)\]

y \[p_0(x)=p_0(x;\beta)=1-p_1(x;\beta),\] donde $\beta=(\beta_0,\beta_1, \beta_2, \cdots, \beta_p)$.

Ejemplo

Consideremos nuestro ejemplo de impago. Podemos examinar qué tipo de probilidades obtendríamos con regresión logística y distintos parametros beta:

crear_p <- function(beta_0, beta_1){
    function(x){
        h(beta_0 + beta_1 * x)
    }
}
df_grid <- tibble(x = seq(0, 1, 0.01))
betas <- tibble(beta_0 = c(-5, -0.5, 2.5),
                beta_1 = c(10,   -2, -4))
betas <- betas |> 
    mutate(p = map2(beta_0, beta_1, crear_p)) |> 
    mutate(grid = map(p, ~ df_grid |> mutate(p_1 = .(x)))) |> 
    select(-p) |> 
    mutate(fun_nom = paste(beta_0, "+", beta_1, "x")) |> 
    unnest(cols = c(grid))
graf_1 + geom_line(data = betas, aes(x = x, y = p_1)) + facet_wrap(~fun_nom)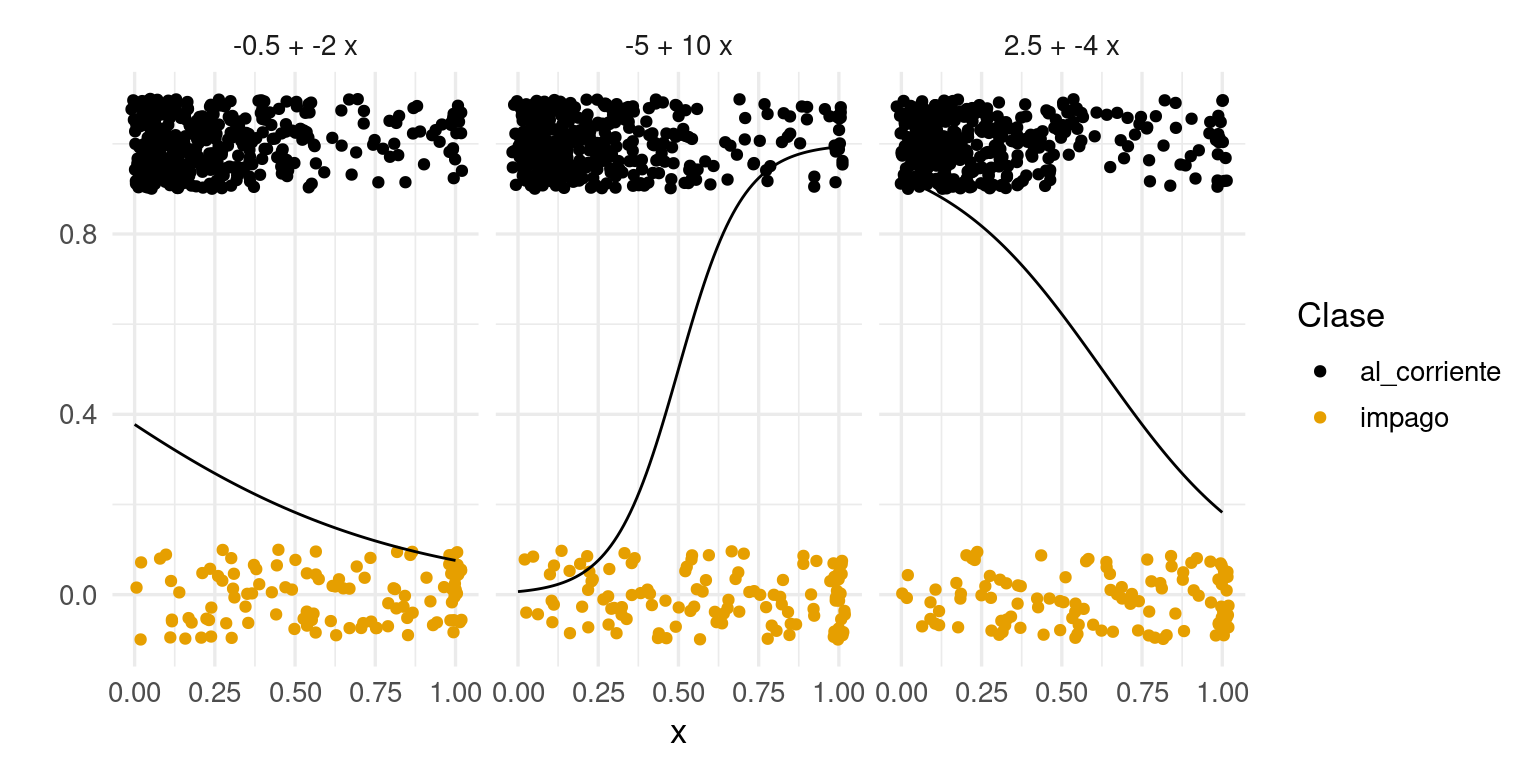

Experimenta con otros valores de $\beta_0$ y $\beta_1$.

Tip

Encontramos los coeficientes de la regresión logística minimizando la pérdida logarítmica de entrenamiento.

Esto se puede hacer de diversas maneras. Tradicionalmente, se utiliza el método de Newton-Raphson, pero resulta más fácil escalar métodos derivados de descenso máximo. Es decir, calculamos el gradiente de la pérdida y tomamos un paso en la dirección contraria al gradiente, que es la dirección local de descenso máximo.

8.8 Ejercicio: datos de diabetes

Ya están divididos los datos en entrenamiento y prueba

diabetes_ent <- as_tibble(MASS::Pima.tr)
diabetes_pr <- as_tibble(MASS::Pima.te)
diabetes_ent |> head() |> gt()

npreg	glu	bp	skin	bmi	ped	age	type
5	86	68	28	30.2	0.364	24	No
7	195	70	33	25.1	0.163	55	Yes
5	77	82	41	35.8	0.156	35	No
0	165	76	43	47.9	0.259	26	No
0	107	60	25	26.4	0.133	23	No
5	97	76	27	35.6	0.378	52	Yes

diabetes_ent$id <- 1:nrow(diabetes_ent)
diabetes_pr$id <- 1:nrow(diabetes_pr)

Aunque no es necesario, podemos normalizar:

receta_diabetes <- recipe(type ~ ., diabetes_ent) |>
  update_role(id, new_role = "id_variable") |> 
  step_normalize(all_numeric()) 
diabetes_ent_s <- receta_diabetes |> prep() |> juice() 
diabetes_pr_s <- receta_diabetes |> prep() |> bake(diabetes_pr)

modelo_lineal <- logistic_reg(mode = "classification") |> 
  set_engine("glm")
flujo_diabetes <- workflow() |> 
  add_model(modelo_lineal) |> 
  add_recipe(receta_diabetes)
flujo_ajustado <- fit(flujo_diabetes, diabetes_ent)
saveRDS(flujo_ajustado, "cache/flujo_ajustado_diabetes.rds")
flujo_ajustado

══ Workflow [trained] ══════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
1 Recipe Step

• step_normalize()

── Model ───────────────────────────────────────────────────────────────────────

Call:  stats::glm(formula = ..y ~ ., family = stats::binomial, data = data)

Coefficients:
(Intercept)        npreg          glu           bp         skin          bmi  
   -0.95583      0.34734      1.01705     -0.05473     -0.02247      0.51263  
        ped          age  
    0.55928      0.45201  

Degrees of Freedom: 199 Total (i.e. Null);  192 Residual
Null Deviance:      256.4 
Residual Deviance: 178.4    AIC: 194.4

Ahora calculamos devianza de prueba y error de clasificación:

preds_prueba <- 
  predict(flujo_ajustado, diabetes_pr, type= "prob") |> 
  bind_cols(predict(flujo_ajustado, diabetes_pr)) |> 
  bind_cols(diabetes_pr |> select(type))
preds_prueba

# A tibble: 332 × 4
   .pred_No .pred_Yes .pred_class type 
      <dbl>     <dbl> <fct>       <fct>
 1    0.232    0.768  Yes         Yes  
 2    0.960    0.0403 No          No   
 3    0.975    0.0253 No          No   
 4    0.959    0.0413 No          Yes  
 5    0.204    0.796  Yes         Yes  
 6    0.265    0.735  Yes         Yes  
 7    0.590    0.410  No          Yes  
 8    0.780    0.220  No          No   
 9    0.558    0.442  No          No   
10    0.798    0.202  No          Yes  
# ℹ 322 more rows

levels(preds_prueba$type)

[1] "No"  "Yes"

# ponemos event_level si "positivo" no es el primer factor
metricas <- metric_set(accuracy, mn_log_loss)
metricas(preds_prueba, truth = type, .pred_Yes, estimate = .pred_class, 
         event_level = "second")

# A tibble: 2 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 accuracy    binary         0.801
2 mn_log_loss binary         0.441

Vamos a repetir usando keras.

library(keras)
x_ent <- diabetes_ent_s |> select(-type, -id) |> as.matrix()
y_ent <- diabetes_ent_s$type == "Yes"
x_prueba <- diabetes_pr_s |> select(-type, -id) |> as.matrix()
y_prueba <- diabetes_pr_s$type == 'Yes'
# definición de estructura del modelo (regresión logística)
# es posible hacerlo con workflows como vimos arriba, 
# pero aquí usamos directamente la interfaz de keras en R
n_entrena <- nrow(x_ent)
modelo_diabetes <- keras_model_sequential() |>
        layer_dense(units = 1,        #una sola respuesta,
            activation = "sigmoid",    # combinar variables linealmente y aplicar función logística
            kernel_initializer = initializer_constant(0), #inicializamos coeficientes en 0
            bias_initializer = initializer_constant(0))   #inicializamos ordenada en 0
# compilar seleccionando cantidad a minimizar, optimizador y métricas
modelo_diabetes |> compile(
        loss = "binary_crossentropy",  # devianza es entropía cruzada
        optimizer = optimizer_sgd(learning_rate = 0.75), # descenso en gradiente
        metrics = list("binary_crossentropy"))
# Ahora iteramos
# Primero probamos con un número bajo de iteraciones
historia <- modelo_diabetes |> fit(
  as.matrix(x_ent), # x entradas
  y_ent,            # y salida o target
  batch_size = nrow(x_ent), # para descenso en gradiente
  epochs = 10 # número de iteraciones
)
plot(historia)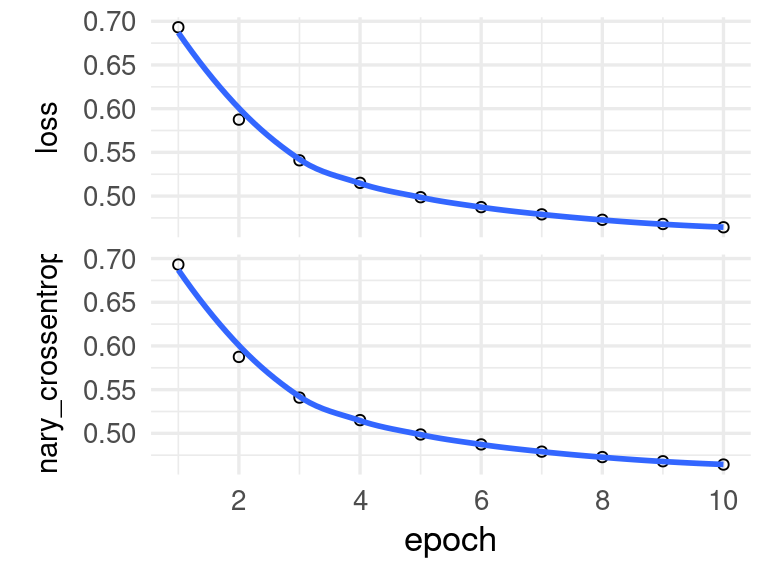

Y ahora podemos correr más iteraciones adicionales:

historia <- modelo_diabetes |> fit(
  as.matrix(x_ent), # x entradas
  y_ent,            # y salida o target
  batch_size = nrow(x_ent), # para descenso en gradiente
  epochs = 1000, # número de iteraciones
  verbose = 0
)

Los errores de entrenamiento y prueba son:

evaluate(modelo_diabetes, x_ent, y_ent)

               loss binary_crossentropy 
          0.4459766           0.4459766

evaluate(modelo_diabetes, x_prueba, y_prueba)

               loss binary_crossentropy 
          0.4406986           0.4406986

Veamos que coeficientes obtuvimos:

get_weights(modelo_diabetes)

[[1]]
            [,1]
[1,]  0.34734303
[2,]  1.01705003
[3,] -0.05472931
[4,] -0.02247147
[5,]  0.51263183
[6,]  0.55927497
[7,]  0.45200703

[[2]]
[1] -0.9558302

que coinciden con los valores que obtuvimos usando regresión logística de glm. La única diferencia es que el algoritmo de optimización que se usa en cada caso es diferente: con keras utilizamos descenso en gradiente, mientras que glm usa Newton-Raphson.

flujo_ajustado |> extract_fit_parsnip()

parsnip model object


Call:  stats::glm(formula = ..y ~ ., family = stats::binomial, data = data)

Coefficients:
(Intercept)        npreg          glu           bp         skin          bmi  
   -0.95583      0.34734      1.01705     -0.05473     -0.02247      0.51263  
        ped          age  
    0.55928      0.45201  

Degrees of Freedom: 199 Total (i.e. Null);  192 Residual
Null Deviance:      256.4 
Residual Deviance: 178.4    AIC: 194.4

8.9 Probabilidades y pérdida 0-1

Otra medida común para medir el error de un clasificador es el error de clasificación, que también llamamos probabilidad de clasificación incorrecta, o error bajo pérdida 0-1.

Probabilidades de clase y pérdida 0-1

Sean $\hat{p}_g(x)$ probabilidades de clase estimadas. El clasificador bajo pérdida 0-1 asociado está dado por \[\hat{g} (x) = \arg\max_g \hat{p}_g(x)\] Podemos estimar su error de clasificación $P(\hat{g}(x) \neq g)$ con una muestra de prueba \[{\mathcal T}=\{ (\mathbf{x}^{(1)},\mathbf{g}^{(1)}),(\mathbf{x}^{(2)},\mathbf{g}^{(2)}), \ldots, (\mathbf{x}^{(m)}, \mathbf{g}^{(m)})\] mediante \[\hat{Err} = \frac{1}{m} \sum_{j=i}^m I(\hat{g}(\mathbf{x}^{(i)}) \neq \mathbf{g}^{(i)}),\] es decir, la proporción de casos de prueba que son clasificados incorrectamente.

Observación: Muy generalmente, esta manera de construir un clasificador es deficiente:

Rara vez queremos clasificar simplemente a la clase con mayor probabilidad. Por ejemplo, podría ser mucho más razonable que basta investigar una operación si su probabilidad de ser fraude está por arriba de 10%, y no necesariamente por arriba de 50%. Esto se debe a que los costos de los distintos errores no son simétricos.
La tasa de clasificación incorrecta por lo tanto es un resumen poco relevante para muchos problemas.
Para la mayoría de problemas de clasificación, es un error ignorar las probabilidades de clase estimadas. No es lo mismo que un cliente tenga 99% de probabilidad de mantenerse al corriente que otro que tiene 55%. Ambos son clasificados de la misma manera por el clasificador de máxima probabilidad.
Puede haber dos predictores con tasas similares de clasificación incorrecta, pero distintos en cuanto a score de Brier o pérdida logarítmica, y mejor score de Brier y pérdida logarítmica indican muchas veces mejor separación de clases.

Más adelante veremos cómo construir reglas de clasificación a partir de probabilidades, pero por el momento notamos que tomar decisiones de cómo clasificar en el proceso de construcción de predictores es mala idea, pues confundimos el desempeño predictivo con los costos de tomar cada decisión de clasificación. Esos costos muchas veces no están perfectamente planteados, de forma que es mejor usar probabilidades para presentar a tomadores de decisiones o calcular simulaciones de costo-beneficio.

Ejemplo

Veamos cómo se comporta en términos de error de clasificación nuestro último modelo:

dat_log_loss |> 
  bind_cols(predict(ajuste_vmc, dat_ent)) |> 
  mutate(correcto = .pred_class == g)  |>  
  ungroup() |>  summarise(p_correctos = mean(correcto))  |> 
  mutate(error_clasif = 1 - p_correctos)

# A tibble: 1 × 2
  p_correctos error_clasif
        <dbl>        <dbl>
1       0.794        0.206

Y calculamos el error de clasificación de prueba:

dat_log_loss_prueba |> 
  bind_cols(predict(ajuste_vmc, dat_prueba)) |> 
  mutate(correcto = .pred_class == g)  |>  
  ungroup() |>  summarise(p_correctos = mean(correcto))  |> 
  mutate(error_clasif = 1 - p_correctos)

# A tibble: 1 × 2
  p_correctos error_clasif
        <dbl>        <dbl>
1       0.802        0.198

8.10 Regresión logística multinomial

Para estimar $K$ probabilidades de clase, consideramos $k$ predictores lineales individuales

\[f_k(x) = \beta_{0, k} + \beta_{1,k} x_1 + \cdots + \beta_{p,k} x_p\]

y la probabilidad de clase la calculamos haciendo softmax sobre estas:

\[p_k(x) = \frac{e^{f_k(x)}}{\sum_i e^{f_i(x)}}\]

que necesariamente suman uno. Nótese si embargo que este modelo está sobreparametrizado, pues solamente es necesario escribir $K-1$ de estas probabilidades, y la última tiene que ser el complemento para que sumen uno. Podemos ver esto, por ejemplo, si sumamos $h(x) = \gamma_0 + \gamma_1x_1 + \cdots \gamma_p x_p$ a todas las funciones:

\[p_k(x) = \frac{e^{f_k(x) + h(x)}}{\sum_i e^{f_i(x) + h(x)}} = \frac{e^{f_k(x)}}{\sum_i e^{f_i(x)}}\]

En regresión logística, por ejemplo, si tenemos $f_1(x)$ y $f_0(x)$ podemos tomar $f_0(x) = 0$, de forma que \[p_1(x) = \frac{e^{f_1(x)}}{1+ e^{f_1(x)}}\] que es justamente el modelo de regresión logística como lo escribimos arriba. Siempre es posible entonces crear una clase de referencia, con coeficientes igual a 0, aunque esto no es necesario si usamos regularización, que generalmente es el caso.

8.11 Ejemplo: clasificación de ropa

Para el siguiente problema tenemos imágenes en blanco y negro de artículos de ropa

library(imager)
ropa_datos <- dataset_fashion_mnist()
ropa_entrena <- ropa_datos$train 
ropa_prueba <- ropa_datos$test
# estas son las categorias:
articulos <- c("playera/top", "pantalón", "suéter", "vestido", "abrigo", "sandalia", 
                 "camisa", "tenis", "bolsa", "bota")
etiquetas_tbl <- tibble(
  codigo = 0:9, 
  articulo = c("playera", "pantalón", "suéter", "vestido", "abrigo", "sandalia", 
                 "camisa", "tenis", "bolsa", "bota"))

x <- ropa_entrena$x
y <- ropa_entrena$y

Por ejemplo:

par(mfrow = c(4, 4), mar = c(1,1,1,1))
for(i in 2:17) plot(as.cimg(t(x[2 + i, ,])), axes = FALSE, main = articulos[y[2 + i] + 1])

Utilizaremos regresión logistica multinomial con keras y regularización L2:

num_classes <- 10
input_shape <- c(28, 28, 1)

# normalizar
x_entrena <- ropa_entrena$x / 255
x_prueba <- ropa_prueba$x / 255
y_entrena <- to_categorical(ropa_entrena$y, num_classes)
y_prueba <- to_categorical(ropa_prueba$y, num_classes)
if(FALSE){
#' Model definition
#' (architecture taken from 
#' https://keras.rstudio.com/articles/examples/mnist_cnn.html )
modelo_ropa <- keras_model_sequential()
modelo_ropa |> 
  layer_flatten() |> 
  layer_dense(units = 10,
              activity_regularizer = regularizer_l2(l = 0.0005), 
              activation = 'softmax') 
# compile model
modelo_ropa |>  compile(
  loss = "categorical_crossentropy",
  optimizer = optimizer_adam(learning_rate = 0.0005),
  metrics = c("accuracy")
)

# train and evaluate
modelo_ropa |> fit(
  x_entrena, y_entrena,
  batch_size = 128,
  epochs = 40,
  verbose = 1,
  validation_data = list(x_prueba, y_prueba)
  )
save_model_tf(modelo_ropa, "cache/red_ropa_1")
}

modelo_ropa <- load_model_tf("cache/red_ropa_1")
scores <- modelo_ropa |> evaluate(
  x_prueba, y_prueba, verbose = 0
)
cat('Test pérdida:', scores[[1]], '\n')

Test pérdida: 0.4358351

cat('Test clasificación correcta:', scores[[2]], '\n')

Test clasificación correcta: 0.8478

Ahora podemos hacer predicciones:

preds_mat <- predict(modelo_ropa, x_prueba)
dim(preds_mat)

[1] 10000    10

probs <- round(preds_mat[1,], 3)
tibble(articulo = articulos, prob = probs) |> 
  arrange(probs)

# A tibble: 10 × 2
   articulo     prob
   <chr>       <dbl>
 1 playera/top 0    
 2 pantalón    0    
 3 suéter      0    
 4 vestido     0    
 5 abrigo      0    
 6 camisa      0    
 7 bolsa       0.005
 8 tenis       0.051
 9 sandalia    0.117
10 bota        0.827

plot(as.cimg(t(ropa_prueba$x[1,,])), axes = FALSE, main = articulos[ropa_prueba$y[1] + 1])