5 Sistemas de recomendación y filtrado colaborativo

En esta sección discutiremos métodos que se pueden utilizar para hacer recomendaciones de documentos, películas, artículos, etc. a personas según sus intereses.

Problema: predecir la respuesta de personas a estímulos a los que no han sido expuestos, basados en respuesta a otros estímulos de esta y quizá otras personas similares.

Por ejemplo, si consideramos usuarios de Netflix: ¿qué tanto le puede gustar a X la película Y? Usuarios de Amazon: ¿qué tan probable es que compren Z artículo si se les ofrece?

5.1 Enfoques de recomendación

Hay varios enfoques que podemos utilizar para atacar este problema:

Principalmente basados en contenido: En función de características de los estímulos, productos o películas (por ejemplo, género, actores, país de origen, año, etc.) intentamos predecir el gusto por el estímulo. En este enfoque, construimos variables derivadas del contenido de los artículos (por ejemplo: qué actores salen, año, etc. o en textos palabras que aparecen), e intentamos predecir el gusto a partir de esas características.

Ejemplo: Si mu gustó Twilight entonces el sistema recomienda otros dramas+vampiros (” por ejemplo “Entrevista con un vampiro”).

Principalmente colaborativos: utilizamos gustos o intereses de usuarios/artículos similares — en el sentido de que les han gustado los mismos artículos/les gustaron a las mismas personas.

Ejemplo: Me gustó StarWars y Harry Potter, varios otros usuarios a los que también les gustaron estas dos películas también les gustó “Señor de los anillos,” así que recomendamos “Señor de los Anillos.” Entre estos métodos, veremos principalmente métodos basados en reducción de dimensionalidad o modelos de factores latentes: encontrar factores latentes que describan usuarios y películas, y predecimos dependiendo de los niveles de factores latentes de personas y películas.

5.2 Datos

Los datos utilizados para este tipo de sistemas son de dos tipos:

Ratings explícitos dados por los usuarios (por ejemplo, Netflix mucho tiempo fue así: \(1-5\) estrellas)
Ratings implícitos que se derivan de la actividad de los usuarios (por ejemplo, vio la película completa, dio click en la descripción de un producto, etc.).

Ejemplo

Consideramos evaluaciones en escala de gusto: por ejemplo \(1-5\) estrellas, o \(1\)-me disgustó mucho, \(5\)-me gustó mucho, etc.

Podemos representar las evaluaciones como una matriz:

	SWars1	SWars4	SWars5	HPotter1	HPotter2	Twilight
a	3	5	5	2	-	-
b	3	-	4	-	-	-
c	-	-	-	5	4	-
d	1	-	2	-	5	4

Y lo que queremos hacer es predecir los valores faltantes de esta matriz, y seleccionar para cada usuario los artículos con predicción más alta, por ejemplo

	SWars1	SWars4	SWars5	HPotter1	HPotter2	Twilight
a	3	5	5	2	3	2.5
b	3	4.6	4	3.9	4.4	4
c	1.3	2.5	2.5	5	4	1.5
d	1	3.2	2	1.7	5	4

Podemos pensar en este problema como uno de imputación de datos faltantes. Las dificultades particulares de este problema son:

Datos ralos: cada usuario sólo ha visto y calificado una proporción baja de películas, y hay películas con pocas vistas.
Escalabilidad: el número de películas y usuarios es generalmente grande

Por estas razones, típicamente no es posible usar técnicas estadísticas de imputación de datos (como imputación estocástica basada en regresión)

Usaremos mejor métodos más simples basados en similitud entre usuarios y películas y descomposición de matrices.

5.3 Modelos de referencia y evaluación

Vamos a comenzar considerando modelos muy simples. El primero que se nos puede ocurrir es uno de homogeneidad de gustos: para una persona \(i\), nuestra predicción de su gusto por la película \(j\) es simplemente la media de la película \(j\) sobre todos los usuarios que la han visto.

Este sería un buen modelo si los gustos fueran muy parecidos sobre todos los usuarios. Esta sería una recomendación de “artículos populares.”

Introducimos la siguente notación:

\(x_{ij}\) es la evaluación del usuario \(i\) de la película \(j\). Obsérvese que muchos de estos valores no son observados (no tenemos información de varias \(x_{ij}\)).
\(\hat{x}_{ij}\) es la predicción que hacemos de gusto del usuario \(i\) por la película \(j\)

En nuestro primer modelo simple, nuestra predicción es simplemente \[\hat{x}_{ij} = \hat{b}_j\] donde \[\hat{b_j} = \frac{1}{N_j}\sum_{s} x_{sj},\] y este promedio es sobre los \(N_j\) usuarios que vieron (y calificaron) la película \(j\).

¿Cómo evaluamos nuestras predicciones?

5.3.1 Evaluación de predicciones

Usamos muestras de entrenamiento y validación. Como en el concurso de Netflix, utilizaremos la raíz del error cuadrático medio:

\[RECM =\left ( \frac{1}{T} \sum_{(i,j) \, observada} (x_{ij}-\hat{x}_{ij})^2 \right)^{\frac{1}{2}}\]

aunque también podríamos utilizar la desviación absoluta media:

\[DAM =\frac{1}{T} \sum_{(i,j) \, observada} |x_{ij}-\hat{x}_{ij}|\]

Nótese que estas dos cantidades se evaluán sólo sobre los pares \((i,j)\) para los que tengamos una observación \(x_{ij}\).

Observaciones:

Generalmente evaluamos sobre un conjunto de validación separado del conjunto de entrenamiento.
Escogemos una muestra de películas, una muestra de usuarios, y ponemos en validación el conjunto de calificaciones de esos usuarios para esas películas.
Para hacer un conjunto de prueba, idealmente los datos deben ser de películas que hayan sido observadas por los usuarios en el futuro (después del periodo de los datos de entrenamiento).
Nótese que no seleccionamos todas las evaluaciones de un usuario, ni todas las evaluaciones de una película. Con estas estrategias, veríamos qué pasa con nuestro modelo cuando tenemos una película que no se ha visto o un usuario nuevo. Lo que queremos ententer es cómo se desempeña nuestro sistema cuando tenemos cierta información de usuarios y de películas.

Ejemplo: datos de Netflix

Los datos del concurso de Netflix originalmente vienen en archivos de texto, un archivo por película.

The movie rating files contain over \(100\) million ratings from \(480\) thousand randomly-chosen, anonymous Netflix customers over \(17\) thousand movie titles. The data were collected between October, \(1998\) and December, \(2005\) and reflect the distribution of all ratings received during this period. The ratings are on a scale from \(1\) to \(5\) (integral) stars. To protect customer privacy, each customer id has been replaced with a randomly-assigned id. The date of each rating and the title and year of release for each movie id are also provided.

The file “training_set.tar” is a tar of a directory containing \(17770\) files, one per movie. The first line of each file contains the movie id followed by a colon. Each subsequent line in the file corresponds to a rating from a customer and its date in the following format:

CustomerID,Rating,Date

MovieIDs range from \(1\) to \(17770\) sequentially.
CustomerIDs range from \(1\) to \(2649429\), with gaps. There are \(480189\) users.
Ratings are on a five star (integral) scale from \(1\) to \(5\).
Dates have the format YYYY-MM-DD.

En primer lugar haremos un análisis exploratorio de los datos para entender algunas de sus características, ajustamos el modelo simple de gustos homogéneos (la predicción es el promedio de calificaciones de cada película), y lo evaluamos.

Comenzamos por cargar los datos:

library(tidyverse)
theme_set(theme_minimal())
cb_palette <- c("#000000", "#E69F00", "#56B4E9", "#009E73", "#F0E442", "#0072B2", "#D55E00", "#CC79A7")

# url <- "https://s3.amazonaws.com/ma-netflix/dat_muestra_nflix.csv"
pelis_nombres <- read_csv('../datos/netflix/movies_title_fix.csv', col_names = FALSE, na = c("", "NA", "NULL"))

## Rows: 17770 Columns: 3

## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (1): X3
## dbl (2): X1, X2

## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

names(pelis_nombres) <- c('peli_id','año','nombre')
dat_netflix <- read_csv( "../datos/netflix/dat_muestra_nflix.csv", progress = FALSE) |> 
    select(-usuario_id_orig) |> 
    mutate(usuario_id = as.integer(as.factor(usuario_id)))

## Rows: 20968941 Columns: 5

## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl  (4): peli_id, usuario_id_orig, calif, usuario_id
## date (1): fecha

## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

head(dat_netflix)

## # A tibble: 6 × 4
##   peli_id calif fecha      usuario_id
##     <dbl> <dbl> <date>          <int>
## 1       1     3 2004-04-14          1
## 2       1     3 2004-12-28          2
## 3       1     4 2004-04-06          3
## 4       1     4 2004-03-07          4
## 5       1     4 2004-03-29          5
## 6       1     2 2004-07-11          6

dat_netflix |> tally()

## # A tibble: 1 × 1
##          n
##      <int>
## 1 20968941

Y ahora calculamos las medias de cada película.

medias_pelis <- dat_netflix |> group_by(peli_id) |> 
    summarise(media_peli = mean(calif), num_calif_peli = n()) 
medias_pelis <- left_join(medias_pelis, pelis_nombres)

## Joining, by = "peli_id"

arrange(medias_pelis, desc(media_peli)) |> 
  top_n(200, media_peli) |> 
  mutate(media_peli = round(media_peli, 2)) |>
  DT::datatable()

Nótese que varias de las películas con mejor promedio tienen muy pocas evaluaciones. Podemos examinar más detalladamente graficando número de evaluaciones vs promedio:

ggplot(medias_pelis, aes(x=num_calif_peli, y=media_peli)) + 
  geom_point(alpha = 0.1) + xlab("Número de calificaciones") + 
  ylab("Promedio de calificaciones")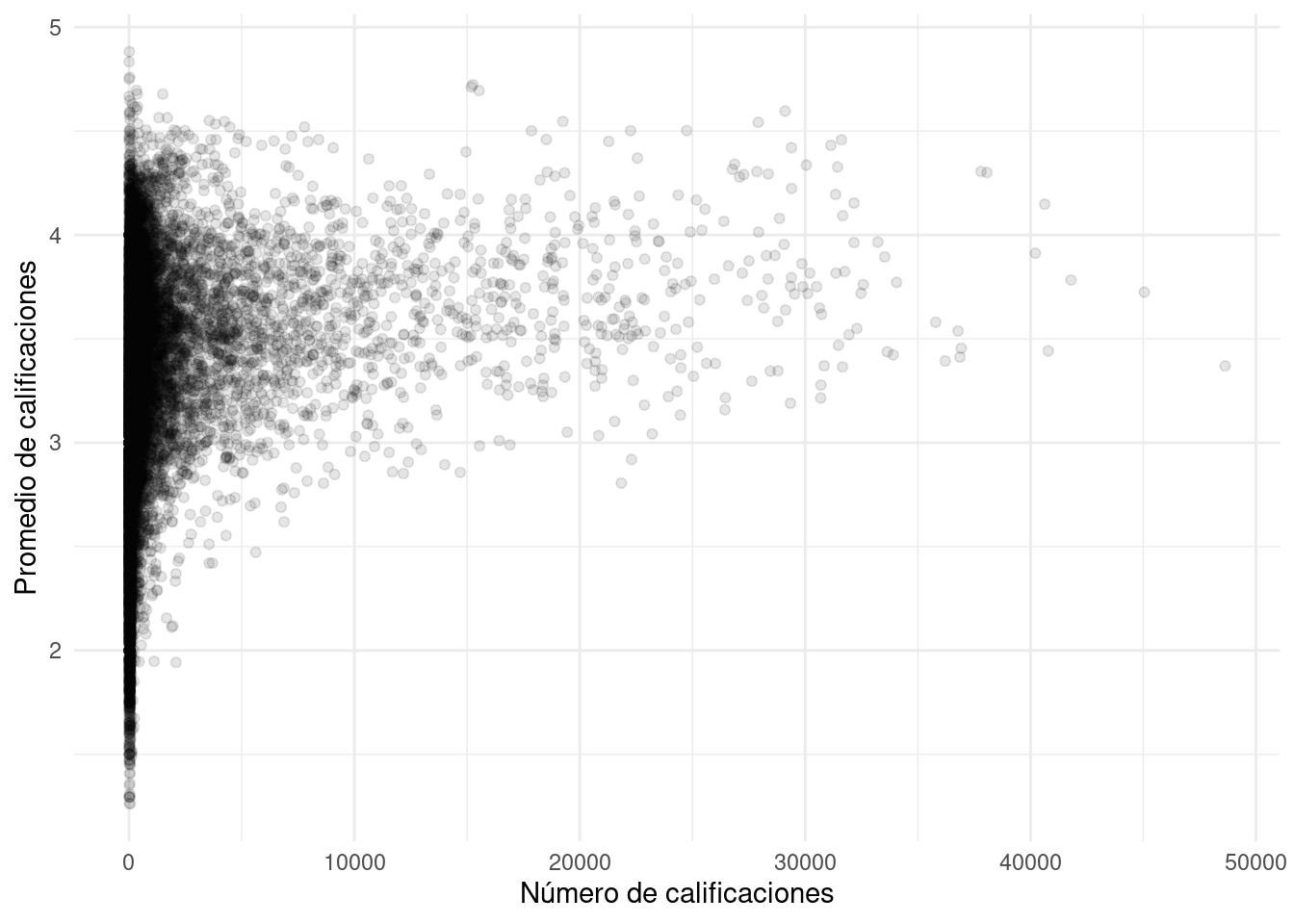

Y vemos que hay más variabilidad en los promedios cuando hay menos evaluaciones, como es de esperarse. ¿Puedes ver algún problema que tendremos que enfrentar con el modelo simple?

Si filtramos por número de calificaciones (al menos \(500\) por ejemplo), estas son las películas mejor calificadas (la mayoría conocidas y populares):

arrange(medias_pelis, desc(media_peli)) |> 
  filter(num_calif_peli > 500) |>
  top_n(200, media_peli) |> 
  mutate(media_peli = round(media_peli, 2)) |>
  DT::datatable()

Ahora seleccionamos nuestra muestra de entrenamiento y de validación. Seleccionamos una muestra de usuarios y de películas:

set.seed(28882)
usuarios <- dat_netflix |> select(usuario_id) |> distinct()
valida_usuarios <- usuarios |> sample_frac(0.2) 
peliculas <-  dat_netflix |> select(peli_id) |> distinct()
valida_pelis <- peliculas |> sample_frac(0.2)

Y separamos calificaciones de entrenamiento y validación:

dat_valida <- dat_netflix |> 
  semi_join(valida_usuarios) |> 
  semi_join(valida_pelis)

## Joining, by = "usuario_id"

## Joining, by = "peli_id"

dat_entrena <- dat_netflix |> 
  anti_join(dat_valida)

## Joining, by = c("peli_id", "calif", "fecha", "usuario_id")

n_valida <- dat_valida |> tally() |> pull(n)
n_entrena <- dat_entrena |> tally() |> pull(n)
sprintf("Entrenamiento: %1d, Validación: %2d, Total: %3d", n_entrena, 
        n_valida, n_entrena + n_valida)

## [1] "Entrenamiento: 20191991, Validación: 776950, Total: 20968941"

Ahora construimos predicciones con el modelo simple de arriba y evaluamos con validación:

medias_pred <- dat_entrena |> group_by(peli_id) |>
  summarise(media_pred = mean(calif)) 
media_total_e <- dat_entrena |> ungroup() |> summarise(media = mean(calif)) |> pull(media)
dat_valida_pred <- dat_valida |> left_join(medias_pred |> collect()) 
head(dat_valida_pred)

## # A tibble: 6 × 5
##   peli_id calif fecha      usuario_id media_pred
##     <dbl> <dbl> <date>          <int>      <dbl>
## 1       2     5 2005-07-18        116       3.64
## 2       2     4 2005-06-07        126       3.64
## 3       2     4 2005-07-30        129       3.64
## 4       2     1 2005-09-07        131       3.64
## 5       2     1 2005-02-13        103       3.64
## 6       8     1 2005-03-21       1007       3.19

Nota que puede ser que algunas películas seleccionadas en validación no tengan evaluaciones en entrenamiento:

table(is.na(dat_valida_pred$media_pred))

## 
##  FALSE 
## 776950

dat_valida_pred <- mutate(dat_valida_pred,
        media_pred = ifelse(is.na(media_pred), media_total_e, media_pred))

No sucede en este ejemplo, pero si sucediera podríamos usar el promedio general de las predicciones. Evaluamos ahora el error:

recm <- function(calif, pred){
  sqrt(mean((calif - pred)^2))
}
error <- dat_valida_pred |> ungroup() |>
  summarise(error = mean((calif - media_pred)^2))
error

## # A tibble: 1 × 1
##   error
##   <dbl>
## 1  1.03

Este error está en las mismas unidades de las calificaciones (estrellas en este caso).

Antes de seguir con nuestra refinación del modelo, veremos algunas observaciones acerca del uso de escala en análisis de datos:

Cuando tratamos con datos en escala encontramos un problema técnico que es el uso distinto de la escala por los usuarios, muchas veces independientemente de sus gustos

Veamos los datos de Netflix para una muestra de usuarios:

# muestra de usuarios
entrena_usu <- sample(unique(dat_entrena$usuario_id), 50)
muestra_graf <- filter(dat_entrena, usuario_id %in% entrena_usu)
# medias generales por usuario, ee de la media
muestra_res <- muestra_graf |> group_by(usuario_id) |>
  summarise(media_calif = mean(calif), 
            sd_calif = sd(calif)/sqrt(length(calif)))
muestra_res$usuario_id <- reorder(factor(muestra_res$usuario_id), muestra_res$media_calif)
ggplot(muestra_res, aes(x=factor(usuario_id), y = media_calif, 
        ymin = media_calif - sd_calif, ymax = media_calif + sd_calif)) + 
  geom_linerange() + geom_point() + xlab('Usuario ID') +
  theme(axis.text.x=element_blank())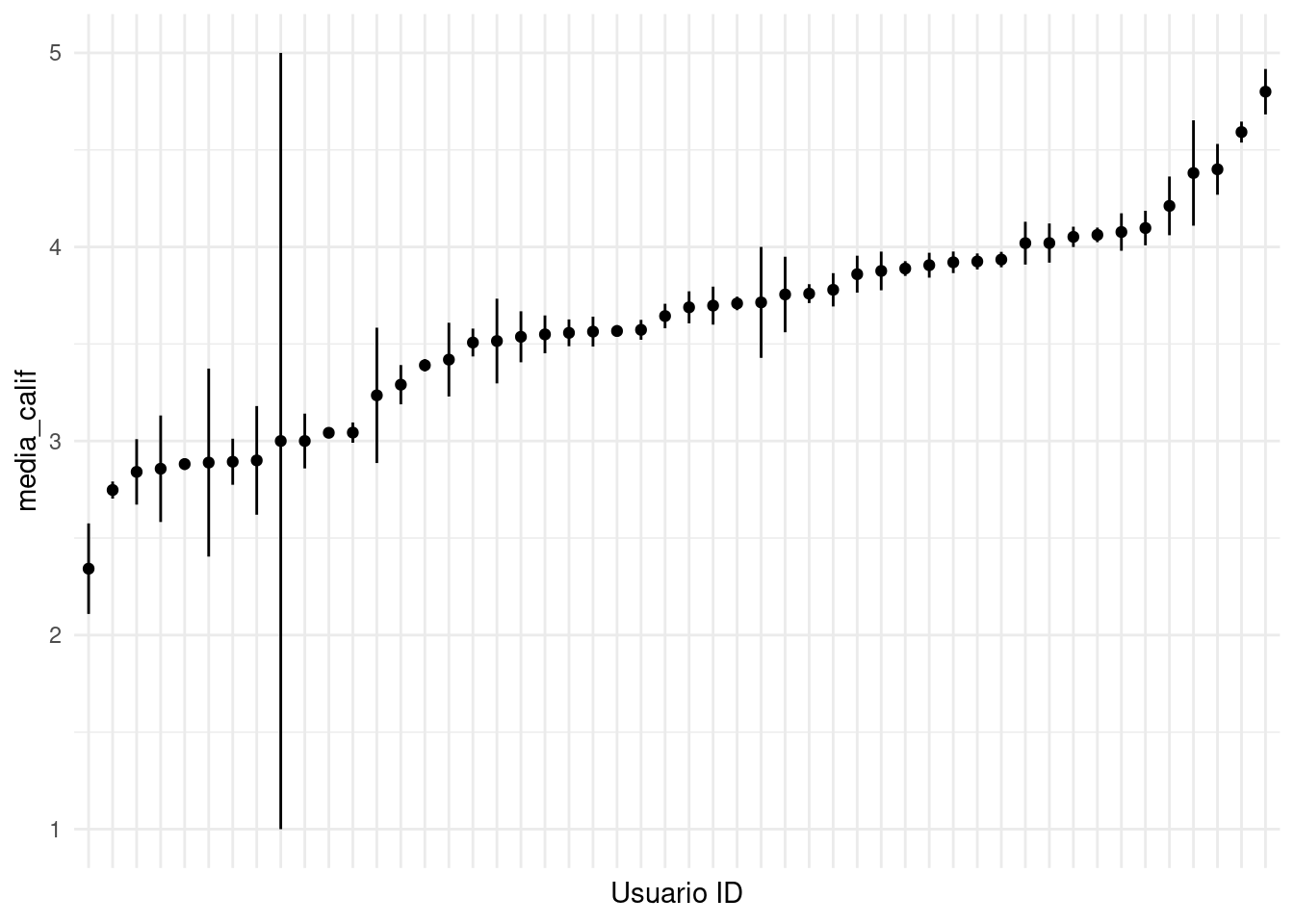

Y notamos que hay unos usuarios que tienen promedios por encima de \(4.5\), mientras que otros califican por debajo de \(3\) en promedio. Aunque esto puede deberse a las películas que han visto, generalmente una componente de esta variabilidad se debe a cómo usa la escala cada usuario.

En primer lugar, quizá uno podría pensar que un modelo base consiste de simplemente predecir el promedio de una película sobre todos los usuarios que la calificaron (sin incluir el sesgo de cada persona). Esto no funciona bien porque típicamente hay distintos patrones de uso de la escala de calificación, que depende más de forma de uso de escala que de la calidad de los items.

Hay personas que son:

Barcos: \(5\),\(5\),\(5\),\(4\),\(4\),\(5\)
Estrictos: \(2\),\(3\),\(3\),\(1\),\(1\),\(2\)
No se compromete: \(3\),\(3\),\(3\),\(3\),\(4\)
Discrimina: \(5\),\(4\),\(5\),\(1\),\(2\),\(4\)

El estilo de uso de las escalas varía por persona. Puede estar asociado a aspectos culturales (países diferentes usan escalas de manera diferente), quizá también de personalidad, y a la forma de obtener las evaluaciones (cara a cara, por teléfono, internet).

Lo primero que vamos a hacer para controlar esta fuente de variación es ajustar las predicciones dependiendo del promedio de calificaciones de cada usuario.

5.3.2 (Opcional) Efectos en análisis de heterogeneidad en uso de escala

Muchas veces se considera que tratar como numéricos a calificaciones en escala no es muy apropiado, y que el análisis no tiene por qué funcionar pues en realidad las calificaciones están en una escala ordinal. Sin embargo,

La razón principal por las que análisis de datos en escala es difícil no es que usemos valores numéricos para los puntos de la escala. Si esto fuera cierto, entonces por ejemplo, transformar una variable con logaritmo también sería “malo.”
La razón de la dificultad es que generalmente tenemos que lidiar con la heterogeneidad en uso de la escala antes de poder obtener resultados útiles de nuestro análisis.

Supongamos que \(X_1\) y \(X_2\) son evaluaciones de dos películas. Por la discusión de arriba, podríamos escribir

\[X_1 = N +S_1,\] \[X_2 = N + S_2,\]

donde \(S_1\) y \(S_2\) representan el gusto por la película, y \(N\) representa el nivel general de calificaciones. Consideramos que son variables aleatorias (\(N\) varía con las personas, igual que \(S_1\) y \(S_2\)).

Podemos calcular

\[Cov(X_1,X_2)\]

para estimar el grado de correlación de gusto por las dos películas, como si fueran variables numéricas. Esta no es muy buena idea, pero no tanto porque se trate de variables ordinales, sino porque en realidad quisiéramos calcular:

\[Cov(S_1, S_2)\]

que realmente representa la asociación entre el gusto por las dos películas. El problema es que \(S_1\) y \(S_2\) son variables que no observamos.

¿Cómo se relacionan estas dos covarianzas?

\[Cov(X_1,X_2)=Cov(N,N) + Cov(S_1,S_2) + Cov(N, S_2)+Cov(N,S_1)\]

Tenemos que \(Cov(N,N)=Var(N)=\sigma_N ^2\), y suponiendo que el gusto no está correlacionado con los niveles generales de respuesta, \(Cov(N_1, S_2)=0=Cov(N_2,S_1)\), de modo que

\[Cov(X_1,X_2)= Cov(S_1,S_2) + \sigma_N^2.\]

donde \(\sigma_N^2\) no tiene qué ver nada con el gusto por las películas.

De forma que al usar estimaciones de \(Cov(X_1,X_2)\) para estimar \(Cov(S_1,S_2)\) puede ser mala idea porque el sesgo hacia arriba puede ser alto, especialmente si la gente varía mucho es un sus niveles generales de calificaciones (hay muy barcos y muy estrictos).

5.3.3 Ejemplo

Los niveles generales de \(50\) personas:

set.seed(128)
n <- 50
niveles <- tibble(persona = 1:n, nivel = rnorm(n,2))

Ahora generamos los gustos (latentes) por dos artículos, que suponemos con correlación negativa:

x <- rnorm(n)
gustos <- tibble(persona=1:n, gusto_1 = x + rnorm(n),
                     gusto_2 = -x + rnorm(n))
head(gustos,3)

## # A tibble: 3 × 3
##   persona gusto_1 gusto_2
##     <int>   <dbl>   <dbl>
## 1       1   0.948   0.459
## 2       2   1.15   -0.676
## 3       3  -1.31    2.58

cor(gustos[,2:3])

##            gusto_1    gusto_2
## gusto_1  1.0000000 -0.5136434
## gusto_2 -0.5136434  1.0000000

Estos dos items tienen gusto correlacionado negativamente:

ggplot(gustos, aes(x=gusto_1, y=gusto_2)) + geom_point() +
    geom_smooth()

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'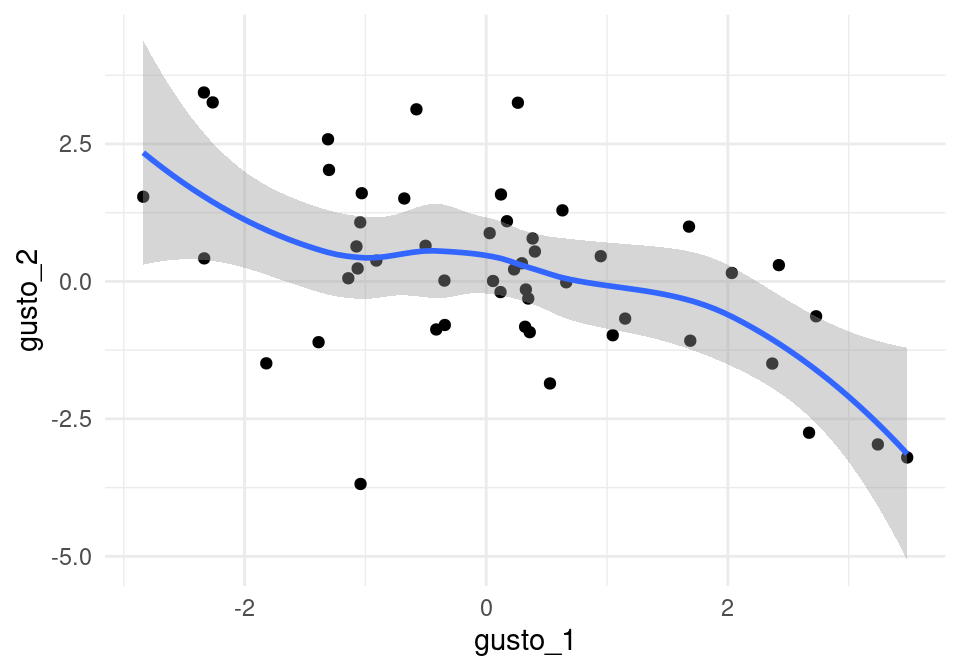

Pero las mediciones no están correlacionadas:

medicion_1 <- niveles$nivel + gustos$gusto_1+rnorm(n,0.3)
medicion_2 <- niveles$nivel + gustos$gusto_2+rnorm(n,0.3)
mediciones <- tibble(persona = 1:n, medicion_1, medicion_2)
cor(mediciones[,2:3])

##             medicion_1  medicion_2
## medicion_1  1.00000000 -0.05825995
## medicion_2 -0.05825995  1.00000000

Así que aún cuando el gusto por \(1\) y \(2\) están correlacionadas negativamente, las mediciones de gusto no están correlacionadas.

ggplot(mediciones, aes(x=medicion_1, y=medicion_2)) +
    geom_point() + geom_smooth()

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'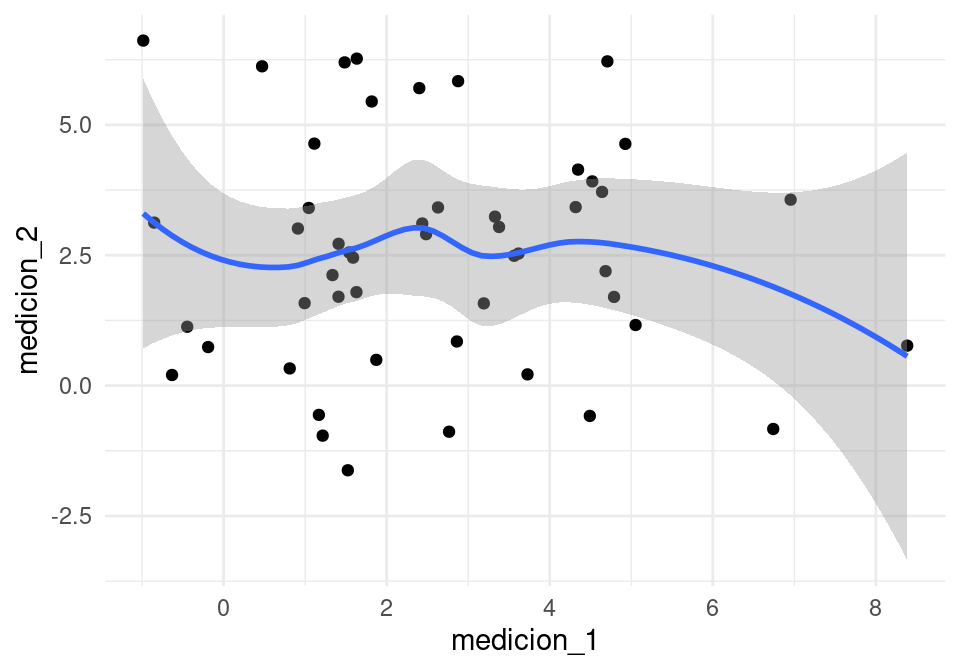

Observaciones: Un modelado más cuidadoso de este tipo de datos requiere más trabajo. Pero para el trabajo usual, generalmente intentamos controlar parte de la heterogeneidad centrando las calificaciones por usuario. Es decir, a cada calificación de una persona le restamos la media de sus calificaciones, que es una estimación del nivel general \(N\). Esta idea funciona si \(k\) no es muy chico.

Si el número de calificaciones por persona (\(k\)) es chico, entonces tenemos los siguientes problemas:

El promedio de evaluaciones es una estimación ruidosa del nivel general.
Podemos terminar con el problema opuesto: nótese que si \(X_1,\ldots, X_k\) son mediciones de gusto distintos items, entonces \[Cov(X_1-\bar{X}, X_2-\bar{X})=Cov(S_1-\bar{S},S_2-\bar{S}),\] \[=Cov(S_1,S_2)-Cov(S_1,\bar{S})-Cov(S_2,\bar{S}) + Var(\bar{S})\]

Si \(k\) es chica, suponiendo que los gustos no están correlacionados, los términos intermedios puede tener valor negativo relativamente grande ( es de orden \(\frac{1}{k}\)), aún cuando el último término sea chico (de orden \(\frac{1}{k^2}\))

Así que ahora las correlaciones estimadas pueden tener sesgo hacia abajo, especialmente si \(k\) es chica.

Más avanzado, enfoque bayesiano: https://www.jstor.org/stable/2670337

5.4 Modelo de referencia

Ahora podemos plantear el modelo base de referencia. Este modelo es útil para hacer benchmarking de intentos de predicción, como primera pieza para construcción de modelos más complejos, y también como una manera simple de producir estimaciones cuando no hay datos suficientes para hacer otro tipo de predicción.

Si \(x_{ij}\) es el gusto del usuario \(i\) por la película \(j\), entonces nuestra predicción es \[\hat{x}_{ij} = \hat{b}_j + (\hat{a}_i-\hat{\mu} ) \] donde \(a_i\) indica un nivel general de calificaciones del usuario \(i\), y \(b_j\) es el nivel general de gusto por la película.

Usualmente ponemos:

Media general \[\hat{\mu} =\frac{1}{T}\sum_{s,t} x_{s,t}\]
Promedio de calificaciones de usuario \(i\) \[\hat{a}_i =\frac{1}{M_i}\sum_{t} x_{i,t} \]
Promedio de calificaciones de la película \(j\) \[\hat{b}_j =\frac{1}{N_j}\sum_{s} x_{s,j}\]

También podemos escribir, en términos de desviaciones:

\[\hat{x}_{ij} = \hat{\mu} + \hat{c}_i + \hat{d}_j \] donde:

Media general \[\hat{\mu} =\frac{1}{T}\sum_{s,t} x_{st}\]
Desviación de las calificaciones de usuario \(i\) respecto a la media general \[\hat{c}_i =\frac{1}{M_i}\sum_{t} x_{it} - \hat{\mu} \]
Desviación de la película \(j\) respecto a la media general \[\hat{d_j} =\frac{1}{N_j}\sum_{s} x_{sj}- \hat{\mu}\]

Una vez que observamos una calificación \(x_{ij}\), el residual del modelo de referencia es \[r_{ij} = x_{ij} - \hat{x_{ij}}\]

Ejercicio: modelo de referencia para Netflix

Calculamos media de películas, usuarios y total:

medias_usuarios <- dat_entrena |> 
    group_by(usuario_id) |>
    summarise(media_usu = mean(calif), num_calif_usu = length(calif)) |> 
    select(usuario_id, media_usu, num_calif_usu)
medias_peliculas <- dat_entrena |> 
    group_by(peli_id) |> 
    summarise(media_peli = mean(calif), num_calif_peli = length(calif)) |> 
    select(peli_id, media_peli, num_calif_peli)
media_total_e <- mean(dat_entrena$calif)

Y construimos las predicciones para el conjunto de validación

dat_valida <- dat_valida |> 
  left_join(medias_usuarios) |>
  left_join(medias_peliculas) |>
  mutate(media_total = media_total_e) |>
  mutate(pred = media_peli + (media_usu - media_total)) |> 
  mutate(pred = ifelse(is.na(pred), media_total, pred))

## Joining, by = "usuario_id"

## Joining, by = "peli_id"

Nótese que cuando no tenemos predicción bajo este modelo para una combinación de usuario/película, usamos el promedio general (por ejemplo).

Finalmente evaluamos

dat_valida |> ungroup() |> summarise(error = recm(calif, pred))

## # A tibble: 1 × 1
##   error
##   <dbl>
## 1 0.929

Observación: ¿Qué tan bueno es este resultado? De wikipedia:

Prizes were based on improvement over Netflix’s own algorithm, called Cinematch, or the previous year’s score if a team has made improvement beyond a certain threshold. A trivial algorithm that predicts for each movie in the quiz set its average grade from the training data produces an RMSE of \(1.0540\). Cinematch uses “straightforward statistical linear models with a lot of data conditioning.”

Using only the training data, Cinematch scores an RMSE of \(0.9514\) on the quiz data, roughly a 10% improvement over the trivial algorithm. Cinematch has a similar performance on the test set, \(0.9525\). In order to win the grand prize of \(1,000,000\), a participating team had to improve this by another \(10%\), to achieve \(0.8572\) on the test set. Such an improvement on the quiz set corresponds to an RMSE of \(0.8563\). Aunque nótese que estrictamente hablando no podemos comparar nuestros resultados con estos números, en los que se usa una muestra de prueba separada de películas vistas despúes del periodo de entrenamiento.

5.5 Filtrado colaborativo: similitud

Además de usar promedios generales por película, podemos utilizar similitud de películas/personas para ajustar predicciones según los gustos de artículos o películas similares. Este es el enfoque más simple del filtrado colaborativo.

Comencemos entonces con la siguiente idea: Supongamos que queremos hacer una predicción para el usuario \(i\) en la película \(j\), que no ha visto. Si tenemos una medida de similitud entre películas, podríamos buscar películas similares a \(j\) que haya visto \(i\), y ajustar la predicción según la calificación de estas películas similares.

Tomamos entonces nuestra predicción base, que le llamamos \(x_{ij}^0\) y hacemos una nueva predicción:

\[\hat{x}_{ij} = x_{ij}^0 + \frac{1}{k}\sum_{t \in N(i,j)} (x_{it} - x_{it}^0 )\]

donde \(N(i,j)\) son películas similares a \(j\) que haya visto \(i\). Ajustamos \(x_{ij}^0\) por el gusto promedio de películas similares a \(j\), a partir de las predicciones base. Esto quiere decir que si las películas similares a \(j\) están evaluadas por encima del esperado para el usuario \(i\), entonces subimos la predicción, y bajamos la predicción cuando las películas similares están evaluadas por debajo de lo esperado.

Nótese que estamos ajustando por los residuales del modelo base. Podemos también utilizar un ponderado por gusto según similitud: si la similitud entre las películas \(j\) y \(t\) es \(s_{jt}\), entonces podemos usar

\[\begin{equation} \hat{x}_{ij} = x_{ij}^0 + \frac{\sum_{t \in N(i,j)} s_{jt}(x_{it} - x_{it}^0 )}{\sum_{t \in N(i,j)} s_{jt}} \tag{5.1} \end{equation}\]

Cuando no tenemos películas similares que hayan sido calificadas por nuestro usuario, entonces usamos simplemente la predicción base.

5.5.1 Cálculo de similitud entre usuarios/películas

Proponemos utilizar la distancia coseno de las calificaciones centradas por usuario. Como discutimos arriba, antes de calcular similitud conviene centrar las calificaciones por usuario para eliminar parte de la heterogeneidad en el uso de la escala.

Ejemplo

	SWars1	SWars4	SWars5	HPotter1	HPotter2	Twilight
a	5	5	5	2	NA	NA
b	3	NA	4	NA	NA	NA
c	NA	NA	NA	5	4	NA
d	1	NA	2	NA	5	4
e	4	5	NA	NA	NA	2

Calculamos medias por usuarios y centramos:

apply(mat.cons,1, mean, na.rm=TRUE)

##        a        b        c        d        e 
## 4.250000 3.500000 4.500000 3.000000 3.666667

mat.c <- mat.cons - apply(mat.cons,1, mean, na.rm=TRUE)
knitr::kable(mat.c, digits = 2)

	SWars1	SWars4	SWars5	HPotter1	HPotter2	Twilight
a	0.75	0.75	0.75	-2.25	NA	NA
b	-0.50	NA	0.50	NA	NA	NA
c	NA	NA	NA	0.50	-0.5	NA
d	-2.00	NA	-1.00	NA	2.0	1.00
e	0.33	1.33	NA	NA	NA	-1.67

Y calculamos similitud coseno entre películas, suponiendo que las películas no evaluadas tienen calificación \(0\):

sim_cos <- function(x,y){
  sum(x*y, na.rm = T)/(sqrt(sum(x^2, na.rm = T))*sqrt(sum(y^2, na.rm = T)))
}
mat.c[,1]

##          a          b          c          d          e 
##  0.7500000 -0.5000000         NA -2.0000000  0.3333333

mat.c[,2]

##        a        b        c        d        e 
## 0.750000       NA       NA       NA 1.333333

sim_cos(mat.c[,1], mat.c[,2])

## [1] 0.2966402

sim_cos(mat.c[,1], mat.c[,6])

## [1] -0.5925503

Observación:

Hacer este supuesto de valores \(0\) cuando no tenemos evaluación no es lo mejor, pero como centramos por usuario tiene más sentido hacerlo. Si utilizaramos las calificaciones no centradas, entonces estaríamos suponiendo que las no evaluadas están calificadas muy mal (\(0\), por abajo de \(1\),\(2\),\(3\),\(4\),\(5\)).
Si calculamos similitud entre usuarios de esta forma, las distancia coseno es simplemente el coeficiente de correlación. Nótese que estamos calculando similitud entre items, centrando por usuario, y esto no es lo mismo que correlación entre columnas.

Ejemplo: ¿cómo se ven las calificaciones de películas similares/no similares?

Centramos las calificaciones por usuario y seleccionamos tres películas que pueden ser interesantes.

dat_entrena_c <- dat_entrena |>
  group_by(usuario_id) |>
  mutate(calif_c = calif - mean(calif))
## calculamos un id secuencial.
dat_entrena_c$id_seq <- as.numeric(factor(dat_entrena_c$usuario_id))
filter(pelis_nombres, str_detect(nombre,'Gremlins'))

## # A tibble: 3 × 3
##   peli_id   año nombre                                 
##     <dbl> <dbl> <chr>                                  
## 1    2897  1990 Gremlins 2: The New Batch              
## 2    6482  1984 Gremlins                               
## 3   10113  2004 The Wiggles: Whoo Hoo! Wiggly Gremlins!

filter(pelis_nombres, str_detect(nombre,'Harry Met'))

## # A tibble: 2 × 3
##   peli_id   año nombre                                 
##     <dbl> <dbl> <chr>                                  
## 1    2660  1989 When Harry Met Sally                   
## 2   11850  2003 Dumb and Dumberer: When Harry Met Lloyd

dat_1 <- filter(dat_entrena_c, peli_id==2897) # Gremlins 2
dat_2 <- filter(dat_entrena_c, peli_id==6482) # Gremlins 1
dat_3 <- filter(dat_entrena_c, peli_id==2660) # WHMS

Juntamos usuarios que calificaron cada par:

comunes <- inner_join(dat_1[, c('usuario_id','calif_c')], dat_2[, c('usuario_id','calif_c')] |> rename(calif_c_2=calif_c))

## Joining, by = "usuario_id"

comunes_2 <- inner_join(dat_1[, c('usuario_id','calif_c')], dat_3[, c('usuario_id','calif_c')] |> rename(calif_c_2=calif_c))

## Joining, by = "usuario_id"

Y ahora graficamos. ¿Por qué se ven bandas en estas gráficas?

ggplot(comunes, aes(x=calif_c, y=calif_c_2)) + 
  geom_jitter(width = 0.2, height = 0.2, alpha = 0.5) + 
  geom_smooth() + xlab('Gremlins 2') + ylab('Gremlins 1')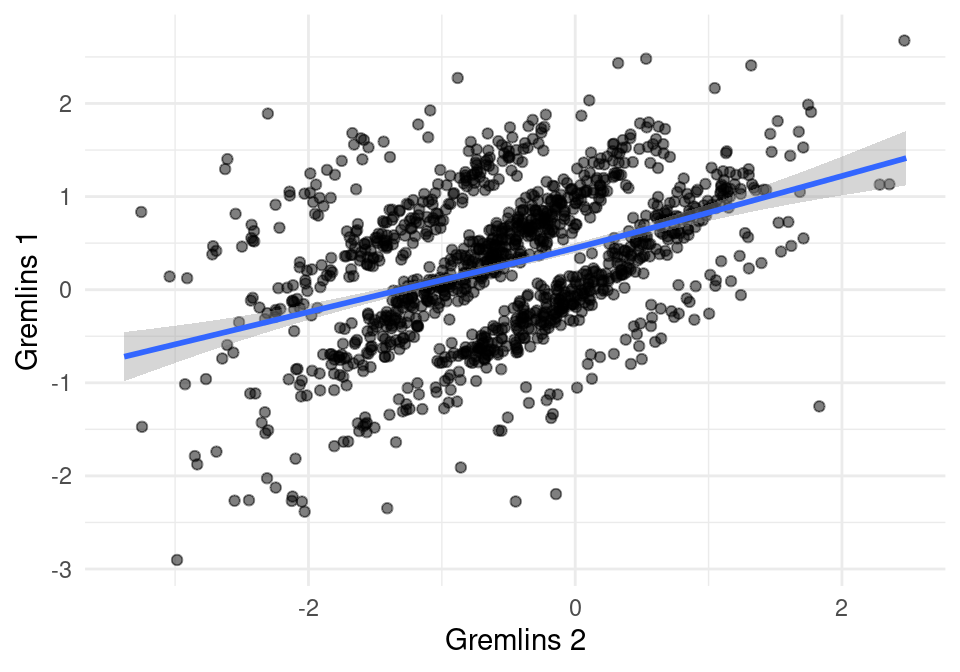

ggplot(comunes_2, aes(x=calif_c, y=calif_c_2))  + 
  geom_jitter(width = 0.2, height = 0.2, alpha = 0.5) + 
  geom_smooth() + xlab('Gremlins 2') + ylab('When Harry met Sally')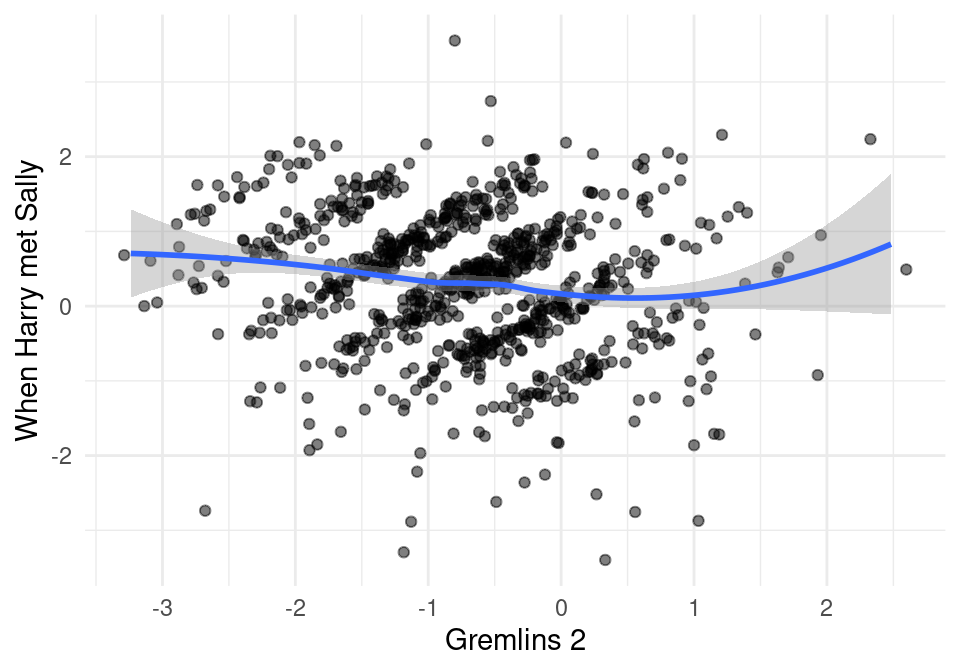

Pregunta: ¿por qué los datos se ven en bandas?

Y calculamos la similitud coseno:

sim_cos(comunes$calif_c, comunes$calif_c_2)

## [1] 0.1769532

sim_cos(comunes_2$calif_c, comunes_2$calif_c_2)

## [1] -0.3156217

Así que las dos Gremlins son algo similares, pero Gremlins \(1\) y Harry Met Sally no son similares.

Podemos ahora seleccionar algunas películas y ver cuáles son películas similares que nos podrían ayudar a hacer recomendaciones:

dat_entrena_2 <- dat_entrena_c |> 
  ungroup() |> 
  select(peli_id, id_seq, calif_c)
ejemplos <- function(pelicula, min_pares = 100){
  mi_peli <- filter(dat_entrena_2, peli_id==pelicula) |> 
             rename(peli_id_1 = peli_id, calif_c_1 = calif_c)
  # vamos a calcular todas las similitudes con mi_peli - esto no es buena
  # idea y discutiremos más adelante cómo evitarlo
  datos_comp <- left_join(dat_entrena_2, mi_peli) |> 
    filter(!is.na(peli_id_1) )
  # calcular similitudes
  out_sum <- datos_comp |> 
      group_by(peli_id) |>
      summarise(similitud = sim_cos(calif_c, calif_c_1), num_pares = n()) |> 
    filter(num_pares > min_pares) |> 
    left_join(pelis_nombres)
  out_sum |> arrange(desc(similitud))  
}

Nótese que las similitudes aparentan ser ruidosas si no filtramos por número de evaluaciones:

ejemplos(8199) |> head(20) |> knitr::kable()

## Joining, by = "id_seq"

## Joining, by = "peli_id"

peli_id	similitud	num_pares	año	nombre
8199	1.0000000	1379	1985	The Purple Rose of Cairo
6247	0.4858263	431	1984	Broadway Danny Rose
16171	0.4670051	618	1987	Radio Days
1058	0.3940953	485	1972	Play it Again Sam
6610	0.3814492	106	1965	The Pawnbroker
17341	0.3748542	545	1983	Zelig
1234	0.3526710	115	1994	Crooklyn
12896	0.3512115	754	1994	Bullets Over Broadway
9540	0.3509817	101	1987	The Decalogue
2599	0.3503702	112	1959	Black Orpheus
16709	0.3480806	342	1980	Stardust Memories
5577	0.3480255	158	1957	Throne of Blood
10605	0.3479292	148	1976	The Front
15808	0.3468051	165	1996	Citizen Ruth
10918	0.3370929	139	1987	Black Adder III
10601	0.3349099	152	1972	The Discreet Charm of the Bourgeoisie
16889	0.3294090	408	1969	Take the Money and Run
6070	0.3217371	117	1989	Black Adder IV
11301	0.3118192	137	1973	The Wicker Man
11720	0.3050482	108	1978	Goin’ South

ejemplos(6807) |> head(20) |> knitr::kable()

## Joining, by = "id_seq"

## Joining, by = "peli_id"

peli_id	similitud	num_pares	año	nombre
6807	1.0000000	2075	1963	8 1/2
16241	0.7429705	677	1960	La Dolce Vita
15303	0.6768162	118	1952	Umberto D.
9485	0.6680970	269	1967	Persona
5605	0.6356236	141	1946	Children of Paradise
15786	0.6017523	564	1957	Wild Strawberries
2965	0.5878489	760	1957	The Seventh Seal
13377	0.5808940	123	1963	Winter Light
10276	0.5738983	654	1950	Rashomon
1708	0.5719259	328	1936	Modern Times
1735	0.5712199	314	1974	Amarcord
7912	0.5677752	243	1960	L’Avventura
12721	0.5674579	283	1952	Ikiru
10661	0.5665439	169	1953	Tokyo Story
17184	0.5612483	240	1939	The Rules of the Game
10277	0.5571376	717	1948	The Bicycle Thief
12871	0.5523090	123	1926	Our Hospitality / Sherlock Jr.
8790	0.5516619	112	1929	Man with the Movie Camera
840	0.5498725	212	1941	The Lady Eve
15016	0.5497364	227	1928	The Passion of Joan of Arc

El problema otra vez es similitudes ruidosas que provienen de pocas evaluaciones en común.

Ejercicio

Intenta con otras películas que te interesen, y prueba usando un mínimo distinto de pares para incluir en la lista

ejemplos(11271)   |> head(20)

## Joining, by = "id_seq"

## Joining, by = "peli_id"

## # A tibble: 20 × 5
##    peli_id similitud num_pares   año nombre                                     
##      <dbl>     <dbl>     <int> <dbl> <chr>                                      
##  1   11271     1          5583  1994 Friends: Season 1                          
##  2    5309     0.944      2679  1997 Friends: Season 4                          
##  3    3078     0.938      3187  1994 The Best of Friends: Season 2              
##  4    5414     0.934      3335  1996 Friends: Season 3                          
##  5    2938     0.930      3000  1994 The Best of Friends: Season 1              
##  6   15307     0.924      2931  1996 The Best of Friends: Season 3              
##  7    8438     0.920      2903  1998 Friends: Season 5                          
##  8    7158     0.919      2094  1997 The Best of Friends: Season 4              
##  9    2942     0.913      2708  1999 Friends: Season 6                          
## 10   15689     0.912      2894  1994 The Best of Friends: Vol. 1                
## 11    9909     0.909      2167  2002 Friends: Season 9                          
## 12    5837     0.908      2554  1999 Friends: Season 7                          
## 13   16083     0.907      1960  1994 The Best of Friends: Vol. 2                
## 14    1877     0.907      3123  1995 Friends: Season 2                          
## 15    1256     0.898      1723  1994 The Best of Friends: Vol. 4                
## 16   15777     0.898      2478  2001 Friends: Season 8                          
## 17   14283     0.886      1544  1994 The Best of Friends: Vol. 3                
## 18    7780     0.858      2481  2004 Friends: The Series Finale                 
## 19   13042     0.629       416  2001 Will & Grace: Season 4                     
## 20    1915     0.623       169  2000 Law & Order: Special Victims Unit: The Sec…

ejemplos(11929)  |> head(20)

## Joining, by = "id_seq"
## Joining, by = "peli_id"

## # A tibble: 20 × 5
##    peli_id similitud num_pares   año nombre                          
##      <dbl>     <dbl>     <int> <dbl> <chr>                           
##  1   11929     1          1955  1997 Anaconda                        
##  2   11687     0.716       274  1994 Street Fighter                  
##  3   15698     0.685       175  1995 Fair Game                       
##  4   13417     0.680       116  1997 Home Alone 3                    
##  5    1100     0.671       169  2000 Dr. T & the Women               
##  6   12149     0.671       708  1997 Speed 2: Cruise Control         
##  7   17221     0.670       645  1993 Look Who's Talking Now          
##  8    5366     0.662       139  1999 The Mod Squad                   
##  9   16146     0.654       146  2003 The Real Cancun                 
## 10    5106     0.652       129  1994 House Party 3                   
## 11   12171     0.648       452  2000 Battlefield Earth               
## 12   16283     0.645       170  1994 Cops & Robbersons               
## 13   15958     0.644       102  1994 Darkman II: The Return of Durant
## 14   12517     0.643       284  2003 Gigli                           
## 15   13607     0.642       137  1992 Stop! Or My Mom Will Shoot      
## 16    1363     0.640       200  1993 Leprechaun                      
## 17   12349     0.639       227  1993 Super Mario Bros.               
## 18    7142     0.637       118  1996 Barb Wire                       
## 19    3573     0.635       286  1993 Cop and a Half                  
## 20    5005     0.634       290  1995 Vampire in Brooklyn

ejemplos(2660)  |> head(20)

## Joining, by = "id_seq"
## Joining, by = "peli_id"

## # A tibble: 20 × 5
##    peli_id similitud num_pares   año nombre                                     
##      <dbl>     <dbl>     <int> <dbl> <chr>                                      
##  1    2660     1         16940  1989 When Harry Met Sally                       
##  2   16722     0.509       149  2001 The Godfather Trilogy: Bonus Material      
##  3   12530     0.458      2861  2004 Sex and the City: Season 6: Part 2         
##  4    8272     0.451       187  1960 The Andy Griffith Show: Season 1           
##  5   14648     0.447       680  2003 Finding Nemo (Full-screen)                 
##  6   11975     0.441       293  2005 Mad Hot Ballroom                           
##  7   16711     0.441      3305  2003 Sex and the City: Season 6: Part 1         
##  8    4427     0.433       744  2001 The West Wing: Season 3                    
##  9   12184     0.430      2676  2002 Sex and the City: Season 5                 
## 10   13073     0.426      2414  1946 It's a Wonderful Life                      
## 11    7639     0.423       171  2004 Star Wars Trilogy: Bonus Material          
## 12   13556     0.422       923  1999 The West Wing: Season 2                    
## 13   14567     0.421       136  1959 Ben-Hur: Collector's Edition: Bonus Materi…
## 14   14550     0.420     11743  1994 The Shawshank Redemption: Special Edition  
## 15     270     0.420      3618  2001 Sex and the City: Season 4                 
## 16    3456     0.419       553  2004 Lost: Season 1                             
## 17    9909     0.418      1763  2002 Friends: Season 9                          
## 18   16674     0.414       103  1994 Forrest Gump: Bonus Material               
## 19    1542     0.410      9277  1993 Sleepless in Seattle                       
## 20   12870     0.408      9397  1993 Schindler's List

5.5.2 Implementación

Si queremos implementar este tipo de filtrado colaborativo (por similitud), el ejemplo de arriba no es práctico pues tenemos que calcular todas las posibles similitudes. Sin embargo, como nos interesa principalmente encontrar los pares de similitud alta, podemos usar LSH:

Empezamos haciendo LSH de las películas usando el método de hiperplanos aleatorios como función hash (pues este es el método que captura distancias coseno bajas). Nuestro resultado son todos los items o películas agrupadas en cubetas. Podemos procesar las cubetas para eliminar falsos positivos (o items con muy pocas evaluaciones).
Ahora queremos estimar el rating del usuario \(i\) de una película \(j\) que no ha visto. Extraemos las cubetas donde cae la película \(j\), y extraemos todos los items.
Entre todos estos items, extraemos los que ha visto el usuario \(i\), y aplicamos el promedio (5.1).

Observaciones

En principio, este análisis podría hacerse usando similitud entre usuarios en lugar de items. En la práctica (ver (Leskovec, Rajaraman, and Ullman 2014)), el enfoque de similitud entre items es superior, pues similitud es un concepto que tiene más sentido en items que en usuarios (los usuarios pueden tener varios intereses traslapados).
Nótese que en ningún momento tuvimos que extraer variables de películas, imágenes, libros, etc o lo que sea que estamos recomendando. Esta es una fortaleza del filtrado colaborativo.
Por otro lado, cuando tenemos pocas evaluaciones o calificaciones este método no funciona bien (por ejemplo, no podemos calcular las similitudes pues no hay traslape a lo largo de usuarios). En este caso, este método puede combinarse con otros (por ejemplo, agregar una parte basado en modelos de gusto por género, año, etc.)

Referencias

Leskovec, Jure, Anand Rajaraman, and Jeffrey David Ullman. 2014. Mining of Massive Datasets. 2nd ed. New York, NY, USA: Cambridge University Press. http://www.mmds.org.