1 Introducción
En este curso principalmente consideraremos técnicas para procesar, analizar y entender conjuntos de datos en dimensión alta (es decir, existen muchos atributos relevantes que describen a cada observación). Tareas básicas en este curso son, por ejemplo:
- Entender si las observaciones forman grupos útiles o interpretables,
- Construir o seleccionar atributos importantes para describir los datos de maneras más simples o útiles,
- En general, descubrir otros tipos de estructuras interesantes en datos de dimensión alta.
Veremos aplicaciones relacionadas con este problema, como
- Análisis de market basket (descubrir características o artículos asociados),
- Sistemas de recomendación (medir similitud entre usuarios o artículos para hacer recomendaciones),
- Búsqueda de elementos muy similares o duplicados,
- Análisis de redes y detección de comunidades,
- Análisis y modelos para lenguaje natural.
En general, consideraremos técnicas que son escalables y se aplican a datos masivos, que son los casos donde la dimensionalidad alta realmente puede explotarse efectivamente. Comenzaremos por describir las dificultades del análisis en dimensión alta.
Simlitud en dimensión alta
Cuando queremos identificar casos similares, o agruparlos por similitud, generalmente estamos pensando alguna tarea que queremos resolver: por ejemplo, recomendar productos o contenido a usuarios similares, detectar imágenes o textos duplicados o reusados, focalizar programas sociales a distintos tipos de hogares o personas, etc.
Muchas veces, identificar los atributos correctos y el tipo de similitud produce herramientas útiles para resolver varios problemas en cada área de interés. Por ejemplo, la medida correcta de similitud de usuarios de Netflix tiene varios usos, igual que la identificación de palabras o pasajes de texto que ocurren en contextos similares.
Consideramos por ejemplo perfiles de actividad en un sitio (Netflix), productos seleccionados por un comprador en un súper, imágenes o textos. En todos estos casos, las observaciones individuales tienen número muy grande de atributos (qué artículos están o no en una canasta, qué películas vio alguien, número de pixeles, o qué palabras ocurren y en qué orden ocurren).
Hay varios problemas que tenemos que manejar en dimensión alta:
- Distintos atributos pueden ser importantes y otros ser no ser relevantes en ciertos grupos o en general. Por ejemplo: si queremos predecir la siguiente palabra en un texto (o traducirlo), la ausencia o presencia de algunas palabras es importantes, y muchas otras palabras son irrelevantes.
- Puede ser que muchos atributos no sean de interés para formar grupos útiles o identificar casos similares.
- Los atributos generalmente tienen relaciones complejas, y no es claro qué medidas de similitud son apropiadas.
Medidas de distancia o similitud
Consideremos la distancia euclideana en dimensión alta. Si generamos una muestra centrada en el origen, las distancias al origen se ve cómo sigue:
library(tidyverse)
centro <- rep(0, 50)
puntos <- MASS::mvrnorm(n = 5000, mu = centro, Sigma = diag(rep(1, 50)))
distancias <- map_dbl(1:nrow(puntos), ~ sqrt(sum((centro - puntos[.x, ])^2)))
qplot(distancias, bins = 30) 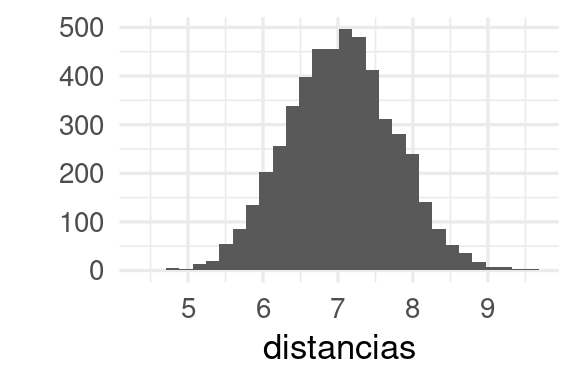
Y vemos que ningún punto está realmente cerca del origen, y las distancias varían alrededor de un valor fijo. Si consideramos todos los posibles pares de puntos, vemos que todos parecen estar más o menos igual de lejos unos de otros:
dist_pares <- dist(puntos) |> as.numeric()
qplot(dist_pares, bins = 30)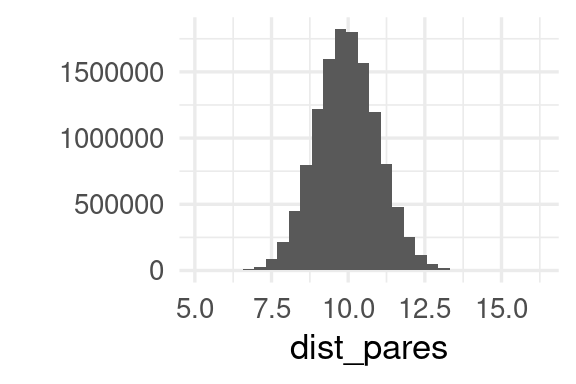
En dimensión alta, nuestra intuición muchas veces no funciona muy bien. Por ejemplo, supongamos que en una dimensión tenemos dos grupos claros:
library(tidyverse)
library(patchwork)
library(glue)
set.seed(10012)
x <- rnorm(100, c( -1,1), c(0.2,0.2))
datos <- tibble(id = 1:100, variable = "x", x = x) |>
mutate(grupo = id %% 2)
ggplot(datos, aes(x = x, fill = factor(grupo))) +
geom_histogram(bins = 30)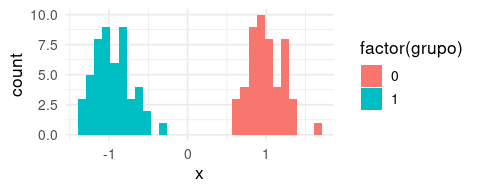
Podemos calcular las distancias entre pares:
distancias_pares <- datos |> select(-id, -grupo) |> dist() |> as.numeric()## Warning in dist(select(datos, -id, -grupo)): NAs introduced by coerciong_1 <- qplot(distancias_pares, bins = 30)Ahora agregamos 50 variables adiconales_
datos_aleatorios <- map_df(1:50, function(i){
datos |> select(id, grupo) |>
mutate(variable = glue("x_{i}"), x = rnorm(100, 0, 1))
})
datos_1 <- bind_rows(datos, datos_aleatorios) |>
pivot_wider(names_from = variable, values_from = x)Y vemos claramente que hay una estructura de grupos en los datos el la gráfica de la izquierda. Sin embargo, si agregamos variables ruidosas, la estructura no es clara y es difícil de recuperar:
distancias_pares_2 <- datos_1 |> select(-id, -grupo) |> dist() |> as.numeric()
g_2 <- qplot(distancias_pares_2, bins = 30)
g_1 + g_2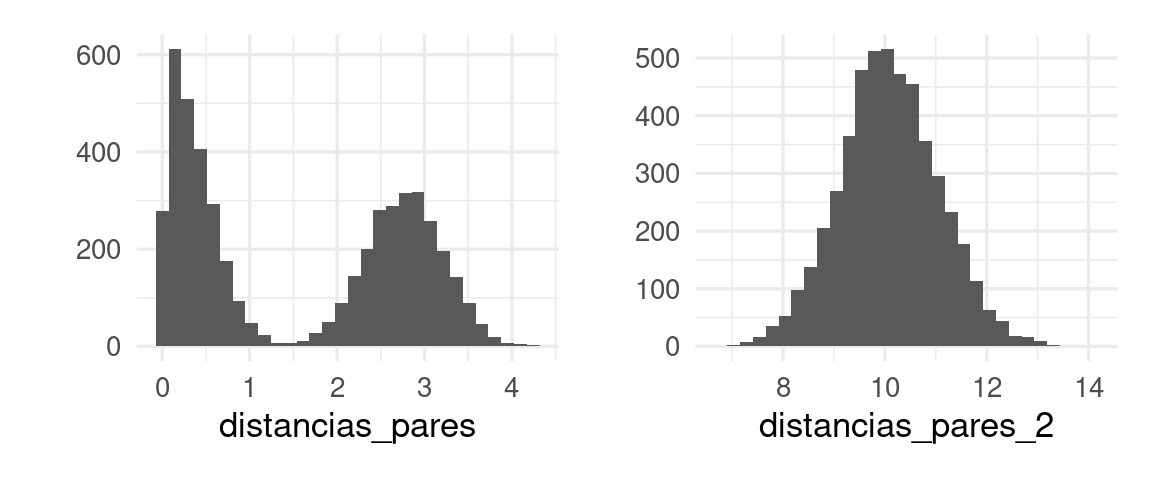
Si usamos un método simple de clustering, no recuperamos los grupos originales:
grupos_km <- kmeans(datos_1 |> select(contains("x")), centers = 2) |>
pluck("cluster")
table(grupos_km, datos_1$grupo)##
## grupos_km 0 1
## 1 38 29
## 2 12 21Tipos de soluciones
Proyección y búsqueda de marginales interesantes
En primer lugar, puede ser que aspectos útiles puedan extraerse de algunas marginales particulares \(P(X_1, X_2)\). Por ejemplo:
- Hay muchas variables ruidosas, en el sentido que no presentan estructuras interesantes o no son útiles para la tarea que nos interesa. (estas paso tiende a ser más guiado por teoría).
- Podemos buscamos regiones \(P(X_1 = x_1, X_2 = x_2)\) alrededor de las cuales se acumula alta probabilidad, o de otra manera: podemos buscar modas de marginales con alta densidad.
Aplicaciones: análisis de conjuntos frecuentes o canastas, selección de características según varianza.
Proyecciones globales
Muchas veces podemos reducir dimensionalidad si reexpresamos variables (ya sea linealmente o no), y luego proyectamos (descomposición en valores singulares, PCA, descomposición de matrices) a regiones de alta densidad.
Aplicaciones: construcción de índices resumen, sistemas de recomendación, indexado semántico latente en análisis de texto.
Descripción de estructura local
En algunos casos, los datos pueden ser del tipo donde la estructura local en pequeñas regiones del espacio de entradas es importante, y algunos casos tienden a acumularse en regiones particulares:
- Duplicados cercanos, búsqueda de vecinos cercanos.
- Análisis de centralidad en redes, búsqueda de comunidades.
- Métodos de reducción de dimensionalidad como t-sne y clustering
Inmersiones (embeddings)
Para algunos tipos de datos, la reducción de dimensionalidad debemos hacerla ad-hoc al problema. Por ejemplo,
- Redes convolucionales de clasificación de imágenes para obtener representaciones en dimensión baja de imágenes (similitud de imágenes).
- Construcción de representaciones donde palabras que ocurren en lugares similares son proyectadas a valores similares (inmersiones de palabras, redes neuronales para NLP).