2 Principios de aprendizaje supervisado

En esta sección examinaremos algunos principios teóricos y de metodología para el aprendizaje supervisado.

2.1 Población y pérdida

Supongamos que tenemos una población grande de observaciones potenciales de la forma

\[(x_1, x_2, \ldots, x_p, y) \]

Y para esa población nos interesa predecir una variable respuesta \(y\) numérica en términos de variables de entrada disponibles \(x = (x_1,x_2,\ldots, x_p)\):

\[(x_1, x_2, \ldots, x_p) \to y\]

El proceso que produce la salida \(y\) a partir de las entradas es típicamente muy complejo y dificíl de describir de forma mecanística (por ejemplo, el ingreso dadas características de los hogares, sus integrantes, condiciones económicas, etc).

Ejemplo

Para ilustrar esta discusión teórica, consideraremos datos simulados. La población está dada por el siguiente proceso generador de datos:

library(tidyverse)
library(tidymodels)
library(patchwork)
library(gt)
genera_datos <- function(n = 500, tipo = NULL){
  dat_tbl <- tibble(nse = runif(n, 0, 100)) |>
    mutate(estudio_años = floor(rnorm(n, 1.5 * sqrt(nse), 1))) |>
    mutate(estudio_años = pmax(0, pmin(17, estudio_años))) |> 
    mutate(habilidad = rnorm(n, 100 + 0.1 * nse, 1)) |> 
    mutate(z = 100 + (habilidad/100) * ( 20 * nse + 5 * (estudio_años))) |> 
    mutate(ingreso = pmax(0, 0.2*(z + rnorm(n, 0, 150))))
  obs_tbl <- dat_tbl |> 
    mutate(tipo = tipo, id = 1:n)
  obs_tbl |> select(id, tipo, x = estudio_años, y = ingreso)
}

Tenemos una sola entrada y una respuesta numérica, y una muestra se ve como sigue:

set.seed(1234)
datos_tbl <- genera_datos(n = 500, tipo = "entrena")
ggplot(datos_tbl, aes(x = x, y = y)) + geom_jitter(width = 0.3) +
  xlab("Años de estudio") + ylab("Ingreso anual (miles)")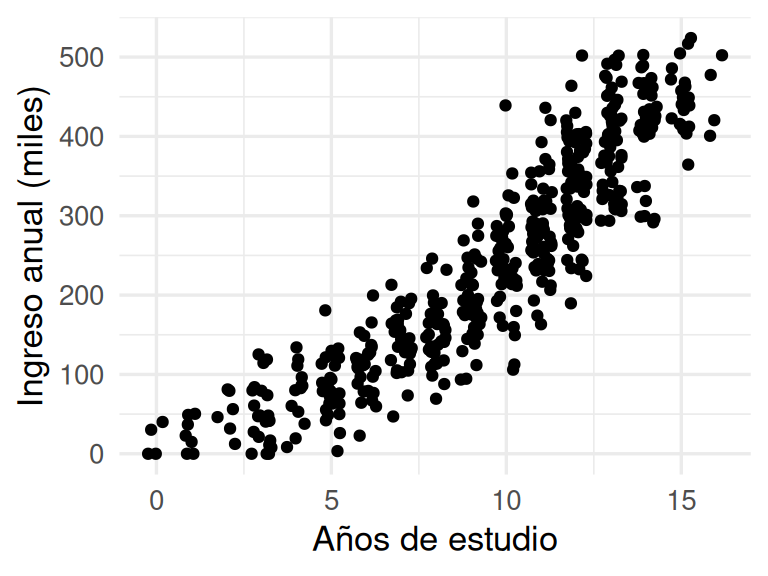

Buscamos construir una función \(f\) tal que si observamos cualquier \(x = (x_1, x_2, \ldots, x_p) \to y\), entonces nuestra predicción es

\[\hat{y} = f(x_1, x_2, \ldots, x_p) = f(x).\] Con esta regla o algoritmo \(f\) queremos predecir con buena precisión el valor de \(y\). Esta \(f\), como explicamos antes, puede ser producida de muy distintas maneras (experiencia, reglas a mano, datos, etc.)

Nuestra primera tarea es definir qué quiere decir predecir con buena precisión.

Para hacer esto tenemos que introducir una medida del error, que llamamos en general función de pérdida.

Función de pérdida y error de predicción

Si el verdadero valor observado es \(y\) y nuestra predicción es \(f(x)\), denotamos la pérdida asociada a esta observación como \[L(y, f(x))\] Para medir el desempeño general de la regla \(f\), consideramos su valor esperado, el error de predicción, que es el promedio sobre toda la población:

\[Err(f) = E[L(y, f(x))]\]

Este es el error que obtendríamos promediando las pérdidas sobre toda la población de interés.

Observación: Para fijar ideas, podríamos usar por ejemplo la pérdida absoluta \(L(y, f(x)) = |y - f(x)|\) o la pérdida cuadrática \(L(y, f(x)) = (y - f(x))^2\).

Observación: en aprendizaje automático, evaluación del error casi siempre es un error promedio. Esto es aceptable cuando no hay riesgos de errores graves, y cuando haremos un número considerable de predicciones en el futuro.

Al menos en teoría, podemos encontrar una \(f\) que minimiza esta pérdida:

Predictor óptimo

Para una población dada, el predictor óptimo (teórico) es

\[f^* = \underset{f}{\mathrm{argmin}} E[L(y, f(x))].\]

Es decir: el mínimo error posible que podemos obtener es \(Err(f^*)\). Para cualquier otro predictor \(f\) tenemos que \(Err(f) \geq Err(f^*).\)

Por ejemplo si usamos la pérdida cuadrática \(L(y, f(x)) = (y - f(x))^2\), entonces puede mostrarse que

\[f^*(x) = E(y | x)\] de forma que \(f^*\) es la media condicional de la \(y\) dado que sabemos que las entradas son \(x\). Si usáramos la pérdida absoluta \(L(y, f(x)) = |y - f(x)|\) entonces \[f^*(x) = \textrm{mediana}(y|x).\] Distintas funciones de pérdida dan distintas soluciones teóricas. Por ejemplo, si existen valores atípicos en \(y\) producidos por errores de registro o medición, usar la pérdida absoluta puede dar mejores resultados que la cuadrática, que tiende a dar mayor peso a errores grandes.

Observaciones:

Podemos ver nuestra tarea entonces como una de ajuste de curvas: queremos aproximar tan bien como sea posible la función \(f^*(x)\).
No es simple decidir qué función de pérdida debería utilizarse para un problema dado de predicción.
Generalmente es una combinación de costos/beneficios del problema que tratamos, conveniencia computacional, y cómo se comportan los errores de nuestros predictores bajo distintas pérdidas. Sin embargo, al principio del proceso de construcción de modelos es mejor escoger una métrica simple que capture a grandes rasgos el comportamiento que esperamos (pérdida cuadrática, absoluta o logarítmica por ejemplo).
Muchas veces es mejor considerar el problema de selección de la pérdida desde dos ángulos: el primero es computacional y de propiedades de la predicción, y el segundo tiene que ver con costos y beneficios asociados al problema que queremos resolver. Para el primero, alguna de las pérdidas estándar (como las que vimos arriba, cuadrática y absoluta, o logarítmica) es usualmente suficiente.
En el segundo ángulo (el de costos y beneficios, o desde el punto de vista de negocio o área de conocimiento), el análisis involucra más aspectos particulares del problema y generalmente tiene que hacerse de manera ad-hoc.

Ejemplo

Supongamos que nos interesa minimizar la pérdida cuadrática. Si tomamos una muestra muy grande (para este problema), podemos aproximar la predicción óptima directamente. Abajo graficamos nuestra muestra chica de datos junto con una buena aproximación del predictor óptimo. En este caso, hacemos simplemente el promedio de las \(y\) para cada valor de \(x\), que funciona razonablemente bien por la muestra grande y la dimensión baja del problema:

poblacion_tbl <- genera_datos(n = 50000, tipo = "poblacion")
# calcular óptimo
preds_graf_tbl <- poblacion_tbl |> 
  group_by(x) |> # condicionar a x
  summarise(.pred = mean(y)) |> # media en cada grupo
  mutate(predictor = "_óptimo")
# graficar con una muestra grande
ggplot(datos_tbl, aes(x = x)) +
  geom_jitter(aes(y = y), colour = "red") + 
  geom_line(data = preds_graf_tbl, aes(y = .pred, colour = predictor), 
    linewidth = 1.1) +
  xlab("Años de estudio") + ylab("Ingreso anual (miles)")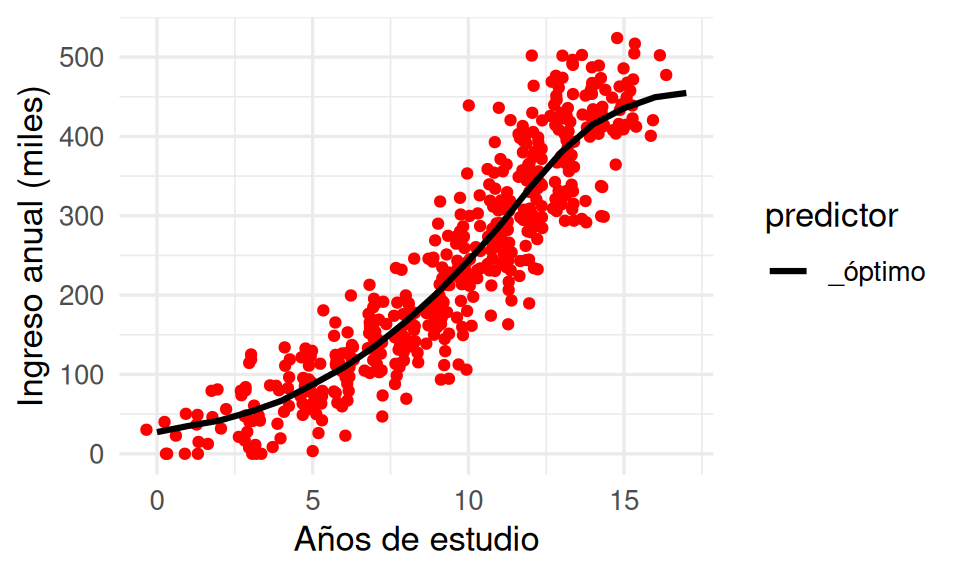

2.2 Estimando el desempeño y datos de prueba

Para obtener una estimación de la pérdida para una función \(f\) que usamos para hacer predicciones, podemos tomar una muestra de datos del proceso generador:

\[{\mathcal T} = \{(\mathbf{x}^{(1)}, \mathbf{y}^{(1)}), (\mathbf{x}^{(2)}, \mathbf{y}^{(2)}), \ldots, (\mathbf{x}^{(m)}, \mathbf{y}^{(m)})\},\]

Compararíamos entonces las respuestas observadas \(\mathbf{y^{(i)}}\) con las predicciones \(f(\mathbf{x^{(i)}})\). Ahora resumimos evaluando el error promedio sobre los datos de prueba. El error de prueba de \(f\) es

\[ \widehat{Err}(f) = \frac{1}{m} \sum_{i=1}^m L(\mathbf{y}^{(i)} , f(\mathbf{x}^{(i)}))\] Por ejemplo, si usamos la pérdida cuadrática,

\[ \widehat{Err}(f) = \frac{1}{m} \sum_{i=1}^m (\mathbf{y}^{(i)} - f(\mathbf{x}^{(i)}))^2\] Si \(m\) es grande, entonces tenemos por la ley de los grandes números que \[Err(f) \approx \widehat{Err} (f)\] Podemos también estimar el error de estimación de \(\widehat{Err}(f)\) con técnicas estándar, por ejemplo bootstrap o aproximación normal.

Obervación: nótese que en estos cálculos no es necesario hacer ningún supuesto acerca de \(f\), que en este argumento está fija y no utiliza la muestra de prueba.

Ejemplo: óptimo

Supongamos que \(f\) es el predictor óptimo que obtuvimos arriba (pero esto aplica para cualquier otra función \(f\) que usemos para hacer predicciones). Tomamos una muestra de prueba, y evaluamos usando la raíz de la pérdida cuadrática media:

prueba_tbl <- genera_datos(n = 2000, tipo = "prueba")
eval_tbl <- prueba_tbl |>  
  left_join(preds_graf_tbl, by = "x") 
resumen_tbl <- eval_tbl |>  
  group_by(predictor, tipo) |> 
  rmse(truth = y, estimate = .pred) 
fmt_resumen <- function(resumen_tbl){
  resumen_tbl |> 
    select(-.estimator) |> 
    pivot_wider(names_from = tipo, values_from = .estimate) |> 
    gt() |> 
    fmt_number(where(is_double), decimals = 0)
}
fmt_resumen(resumen_tbl)

predictor	.metric	prueba
_óptimo	rmse	49

Este es nuestro error de prueba. Como la muestra de prueba no es muy grande, podríamos usar un método estándar para estimar su precisión, por ejemplo con bootstrap.

Ejemplo: regla

Ahora probemos con otro predictor, por ejemplo, supongamos que estamos usando la regla de “cada año de escolaridad aumenta ingresos potenciales en 20 unidades”, un predictor construido con reglas manuales que es

f_regla <- function(x){
  20 * x
}

Abajo lo graficamos en comparación con el modelo óptimo:

años_x <- tibble(x = seq(0, 17, by = 0.5))
preds_regla_tbl <- años_x |> 
  mutate(.pred = f_regla(x), predictor = "regla")
preds_graf_tbl <- bind_rows(preds_regla_tbl, preds_graf_tbl)
ggplot(datos_tbl, aes(x = x)) +
  geom_point(aes(y = y), colour = "red", alpha = 0.2) +
  geom_line(data = preds_graf_tbl, aes(y = .pred, colour = predictor), size = 1.1)

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.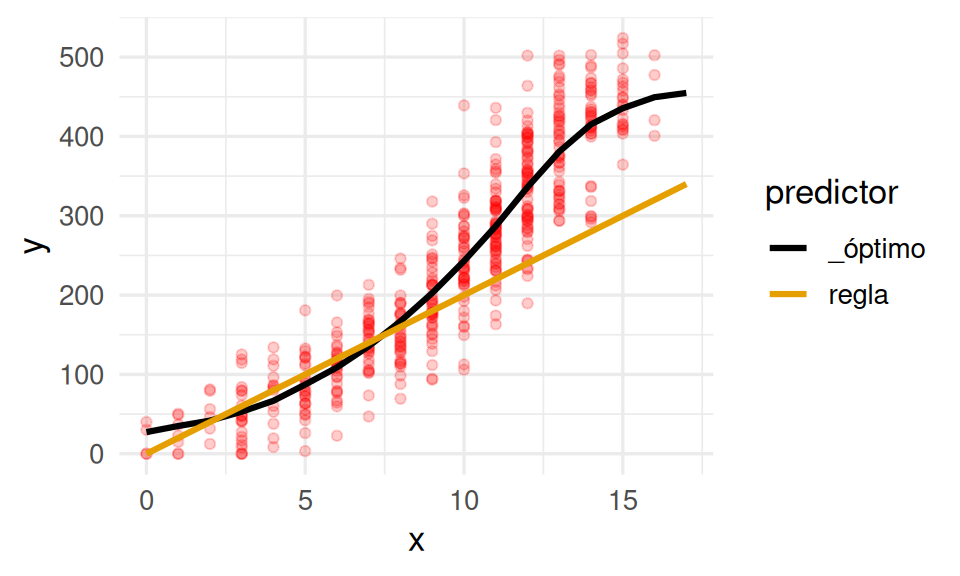

eval_tbl <- prueba_tbl |>  
  left_join(preds_graf_tbl, by = "x", relationship = "many-to-many") 
resumen_tbl <- eval_tbl |>  
  group_by(predictor, tipo) |> 
  rmse(truth = y, estimate = .pred) 
fmt_resumen(resumen_tbl)

predictor	.metric	prueba
_óptimo	rmse	49
regla	rmse	91

Observa que el error es considerablemente mayor que el error que obtuvimos con el predictor óptimo del ejemplo anterior.

2.3 Aprendizaje supervisado

En aprendizaje supervisado, buscamos construir la función \(f\) de manera automática usando datos, de forma que el error de predicción sea lo menor posible. Supongamos entonces que tenemos un conjunto de datos etiquetados (sabemos la \(y\) correspondiente a cada \(x\)):

\[{\mathcal L}=\{ (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}), \ldots, (x^{(N)}, y^{(N)}) \}\]

que llamamos conjunto de entrenamiento.

Un algoritmo de aprendizaje (aprender de los datos automáticamente) es una regla que asigna a cada conjunto de entrenamiento \({\mathcal L}\) una función \(\hat{f}\):

\[{\mathcal L} \to \hat{f} = f_{\mathcal L} \]

Una vez que construimos la función \(\hat{f}\), podemos hacer predicciones.

El desempeño del predictor particular \(\hat{f}\) se mide igual que antes: observamos otra muestra \({\mathcal T}\), que llamamos muestra de prueba,

\[{\mathcal T} = \{(\mathbf{x}^{(1)}, \mathbf{y}^{(1)}), (\mathbf{x}^{(2)}, \mathbf{y}^{(2)}), \ldots, (\mathbf{x}^{(m)}, \mathbf{y}^{(m)})\},\]

y calculamos el error de prueba. Si suponemos que \(m\) es suficientemente grande:

\[ \widehat{Err}(\hat{f}) = \frac{1}{m} \sum_{i=1}^m L(\mathbf{y}^{(i)} , \hat{f}(\mathbf{x}^{(i)})) \]

es una buena aproximación del error de predicción \(Err(\hat{f})\).

Adicionalmente, definimos otra cantidad de menor interés, el error de entrenamiento, como

\[\overline{err} = \frac{1}{N}\sum_{i=1}^N L(y^{(i)} , \hat{f}(x^{(i)})).\] que es una medida de qué tan bien se ajusta a \(\hat{f}\) a los datos con los que se entrenó \(\hat{f}\). Usualmente esta cantidad no es apropiada para medir el desempeño de un predictor, pues el algoritmo \(\hat{f}\) incluye las “respuestas” \(y_i\) en su construcción, de forma que tiende a ser una estimación optimista del error de predicción.

Ejemplo: vecinos más cercanos

Consideremos usar un método de \(k\)-vecinos más cercanos para resolver este problema. Este método es simple: si queremos hacer una predicción en las entradas \(x\), buscamos los puntos de entrenamiento con entradas \(x^{(i)}\) más cercanas a \(x\), que denotamos como \(N_k(x)\). Tomamos las \(y\) correspondientes a estas \(x\) y las usamos para hacer nuestra predicción:

\[f_2(x) = \frac{1}{k}\sum_{x^{(i)} \in N_k(x)} y^{(i)}\]

Primero obtendremos una muestra de entrenamiento:

set.seed(12)
entrena_tbl <- genera_datos(n = 20, tipo = "entrena")

En nuestro ejemplo, utilizaremos 2 vecinos más cercanos:

# modelo
modelo_kvecinos <- nearest_neighbor(
    neighbors = 2, 
    weight_func = "gaussian") |> 
  set_mode("regression") |> 
  set_engine("kknn")
# preprocesamiento
receta <- recipe(y ~ x, data = entrena_tbl |> select(x, y))
# flujo
flujo <- workflow() |> 
  add_recipe(receta) |> 
  add_model(modelo_kvecinos)
# Ajustamos flujo
flujo_ajustado_vecinos <- fit(flujo, entrena_tbl)

Hacemos predicciones y calculamos el error:

eval_tbl <- bind_rows(prueba_tbl, entrena_tbl) 
resumen_vmc_tbl <- 
  predict(flujo_ajustado_vecinos, eval_tbl) |> 
  mutate(predictor = "vecinos") |> 
  bind_cols(eval_tbl) |> 
  group_by(predictor, tipo) |> 
  rmse(truth = y, estimate = .pred) 
fmt_resumen(resumen_vmc_tbl)

predictor	.metric	entrena	prueba
vecinos	rmse	36	65

El error de prueba, que es el que nos interesa hacer chico, es considerablemente grande. Si graficamos podemos ver el problema:

preds_vmc <- predict(flujo_ajustado_vecinos, años_x) |> 
  bind_cols(años_x) |> mutate(predictor = "vecinos")
preds_graf_tbl <- bind_rows(preds_vmc, preds_graf_tbl |> 
  filter(predictor == "_óptimo"))
g_1 <- ggplot(entrena_tbl, aes(x = x)) +
  geom_line(data = preds_graf_tbl |> filter(predictor != "regla"), 
            aes(y = .pred, colour = predictor), size = 1.1) +
  geom_point(aes(y = y), colour = "red") +
  labs(subtitle = "Óptimo vs ajustado")
g_1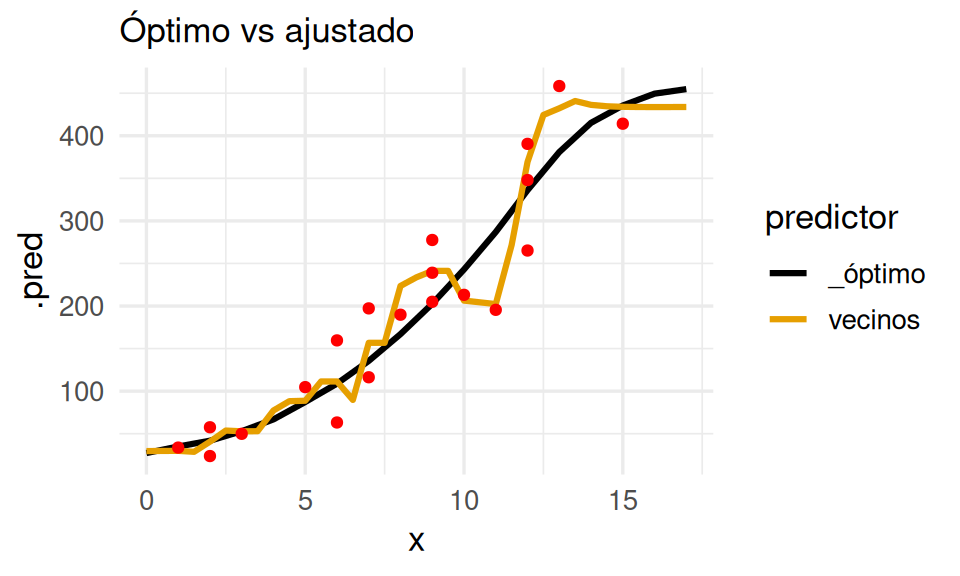

Donde vemos que este método intenta interpolar los datos, capturando ruido y produciendo variaciones que lo alejan del modelo óptimo. Esto lo notamos en lo siguiente:

Hay una brecha grande entre el error de entrenamiento y el error predictivo.
Esta estimación de vecinos más cercanos es muy dependiente de la muestra de entrenamiento que obtengamos, pues intenta casi interpolar los datos. Esto sugiere alta variabilidad de las predicciones dependiendo de la muestra particular de entrenamiento que utilizamos.
Decimos que este predictor está sobreajustado.

Ejemplo: regresión lineal

Ahora intentaremos con un modelo lineal. En este caso, utilizamos un predictor de la forma

\[f(x) = \beta_0 + \beta_1x\] Usamos la muestra de entrenamiento para encontrar la \(\beta_0\) y \(\beta_1\) que minimizar el error sobre los datos disponibles de entrenamiento, lo cual es un problema de optimización relativamente fácil. Usamos entonces \[\hat{f}(x) =\hat{\beta}_0 + \hat{\beta}_1 x\] para hacer nuestras predicciones.

modelo_lineal <- linear_reg() |> 
  set_mode("regression") |> 
  set_engine("lm")
flujo_lineal <- workflow() |> 
  add_recipe(receta) |> 
  add_model(modelo_lineal)
# Ajustamos
flujo_ajustado_lineal <- fit(flujo_lineal, entrena_tbl)

Hacemos predicciones y calculamos el error:

eval_tbl <- bind_rows(prueba_tbl, entrena_tbl) 
resumen_lineal_tbl <- 
  predict(flujo_ajustado_lineal, eval_tbl) |> 
  mutate(predictor = "lineal") |> 
  bind_cols(eval_tbl) |> 
  group_by(predictor, tipo) |> 
  rmse(truth = y, estimate = .pred) 
fmt_resumen(bind_rows(resumen_vmc_tbl, resumen_lineal_tbl))

predictor	.metric	entrena	prueba
vecinos	rmse	36	65
lineal	rmse	49	56

Y el desempeño de este método es mejor que vecinos más cercanos (ver columna de prueba).

preds_1 <- predict(flujo_ajustado_lineal, tibble(x = 0:17)) |> 
  bind_cols(tibble(x = 0:17, predictor = "lineal"))
preds_graf_tbl <- bind_rows(preds_1, preds_graf_tbl)
g_1 <- ggplot(datos_tbl, aes(x = x)) +
  geom_point(aes(y = y), colour = "red", alpha = 0.1) +
  geom_line(data = preds_graf_tbl |> filter(predictor %in% c("_óptimo", "lineal")), 
            aes(y = .pred, colour = predictor), size = 1.1) +
  labs(subtitle = "Óptimo vs ajustado")
g_1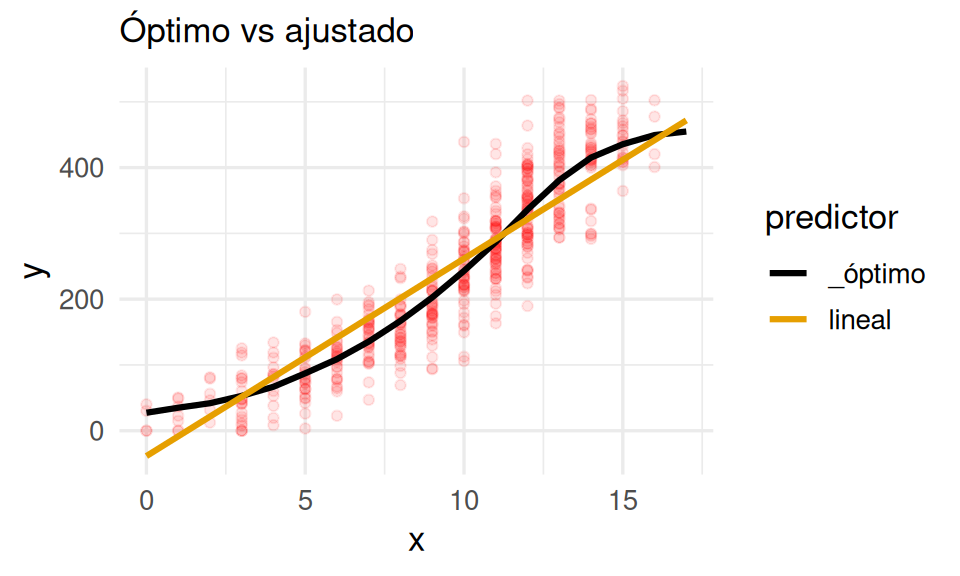

En este caso:

No hay brecha tan grande entre el error de entrenamiento y el error predictivo
Observamos patrones claros de desajuste: el predictor lineal no captura el patrón curvo que presentan los datos: en la parte media de las \(x\) tiende a producir predicciones demasiado altas y lo contario ocurre en los extremos
Decimos que esté modelo presenta subajuste.

2.4 Entendiendo el error de predicción

Para formalizar las observaciones y definiciones anteriores podemos recurrir a la teoría estadística. Aunque consideraremos aquí por facilidad el error cuadrático, los conceptos presentados nos darán una guía para entender cómo mejorar el desempeño de algoritmos de predicción en general.

Cconsideramos entonces los residuales de cada ajuste, para un caso de prueba:

\[\mathbf{y} - \hat{f_{\mathcal{L}}}(\mathbf{x})\] Esta cantidad puede tener un valor positivo o negativo grande, lo que indica errores grandes. Sea \(f^*\) el predictor óptimo, que en el caso de la pérdida cuadrática, como explicamos arriba, es \(f^*(x) = E[Y|X = x]\) . Entonces, en primer lugar:

\[\mathbf{y} - \hat{f_{\mathcal{L}}}(\mathbf{x}) = \underbrace{(f^* (\mathbf{x}) - \hat{f_{\mathcal{L}}}(\mathbf{x}))}_\text{reducible} + \underbrace{(\mathbf{y}- f^*(\mathbf{x}))}_\text{irreducible}.\] donde vemos que si las dos cantidades de la derecha están cercanas a cero, entonces el residual es cercano a cero (la predicción es precisa):

Error irreducible: no depende de nuestro algoritmo, sino de la información que tenemos en \(x\) para predecir \(y\). Si queremos hacer esté error más chico, necesitamos incluir otras variables \(x\) relevantes para predecir \(y\).
Error reducible: qué tan lejos nuestro método está del óptimo. Podemos mejorar este error seleccionando nuestro algoritmo de predicción \(\hat{f}\) (y el tamaño de la muestra de entrenamiento) de manera adecuada.

En nuestros dos ejemplos anteriores, el error reducible era considerablemente grande (como podemos verificar comparando con el predictor óptimo, que sólo sufre de error irreducible). Pero la razón por la que ese error reducible es grande es diferente en cada caso.

Si consideramos pérdida cuadrática, podemos calcular la pérdida promedio condicional a \(\mathbf{x}\) promediando sobre la condicional de \(\mathbf{y}\) dada \(\mathbf{x}\):

\[Err(\hat{f_{\mathcal{L}}}(\mathbf{x})) = E[(\mathbf{y} - \hat{f_{\mathcal{L}}}(\mathbf{x}))^2] = (f^* (\mathbf{x}) - \hat{f_{\mathcal{L}}}(\mathbf{x}))^2 + E[(\mathbf{y}- f^*(\mathbf{x}))^2]\] Que reescribimos como:

\[ Err(\hat{f_{\mathcal{L}}}(\mathbf{x})) = (f^* (\mathbf{x}) - \hat{f_{\mathcal{L}}}(\mathbf{x}))^2 + \sigma^2(\mathbf{x}) \]

Teóricamente es dificil decir algo acerca del primer término del lado derecho de esta ecuación. Sin embargo, podemos avanzar si tomamos el promedio sobre todas las muestras posibles de entrenamiento de tamaño \(n\) que podríamos usar para ajustar \(\hat{f_{\mathcal{L}}}(\mathbf{x})\). Tomando este valor esperado podemos demostrar que el error promedio se escribe como

\[ (f^*(x) - E(\hat{f_{\mathcal{L}}}(\mathbf{x})))^2 + \textrm{Var}(\hat{f_{\mathcal{L}}}(\mathbf{x})) + \sigma^ 2(\mathbf{x})\]

que reescribimos como

\[\textrm{Error(x)} = \textrm{Sesgo}^2(\hat{f_{\mathcal{L}}}(\mathbf{x})) + \textrm{Var}(\hat{f_{\mathcal{L}}}(\mathbf{x})) + \sigma^ 2(\mathbf{x})\]

El error reducible ahora se descompone en dos partes:

El error por sesgo: que se debe a que nuestro algoritmo sistemáticamente estima mal el valor óptimo.
El error por varianza: si las predicciones varían con la muestra, quiere decir que nuestro algoritmo es muy sensible a los datos de entrenamiento, y por lo tanto es difícil que se mantenga cerca del óptimo \(f^*(x)\).

En general, decimos que un algoritmo sufre de sobreajuste si el error por varianza es grande, y sufre de subajuste si el error por sesgo es grande.

En nuestros dos ejemplos, intuímos que vecinos más cercanos sufre más de sobreajuste y regresión lineal de subajuste, lo cual verificamos a continuación.

2.5 Ejemplo: fuentes de error

Vamos a ver qué sucede con nuestros dos métodos si utilizamos varias muestras:

set.seed(82)

modelo_kvecinos <- nearest_neighbor(
    neighbors = 2, 
    weight_func = "gaussian") |> 
  set_mode("regression") |> 
  set_engine("kknn")
flujo_vecinos <- workflow() |> 
  add_recipe(receta) |> 
  add_model(modelo_kvecinos)

ajustes <- map(1:5, function(rep){
  muestra_tbl <- sample_n(poblacion_tbl, 20) |> 
    mutate(tipo = "entrena")
  flujo_ajustado_vecinos <- fit(flujo_vecinos, muestra_tbl)
  flujo_ajustado_lineal <- fit(flujo_lineal, muestra_tbl)
  list(vmc = flujo_ajustado_vecinos, 
       lineal = flujo_ajustado_lineal)
})

Ahora podemos graficar para entender mejor qué está pasando:

datos_tbl <- map_df(1:length(ajustes), function(i){
  ajuste <- ajustes[[i]]
  preds_1 <- predict(ajuste$vmc, tibble(x = 0:17)) |> 
    bind_cols(tibble(x = 0:17, predictor = "vecinos"))
  preds_2 <- predict(ajuste$lineal, tibble(x = 0:17)) |> 
    bind_cols(tibble(x = 0:17, predictor = "lineal"))
  preds_graf_tbl <- bind_rows(preds_1, preds_2) |> 
    mutate(predictor = factor(predictor)) |> 
    mutate(rep = i)
  preds_graf_tbl
})


g_1 <- ggplot(datos_tbl, aes(x = x, y = .pred)) +
  geom_line(aes(group = rep, colour = factor(rep))) + facet_wrap(~predictor) +
  geom_line(data = preds_graf_tbl |> 
            filter(predictor == "_óptimo") |> select(-predictor), size = 1.1) +
  theme(legend.position = "none") 
g_1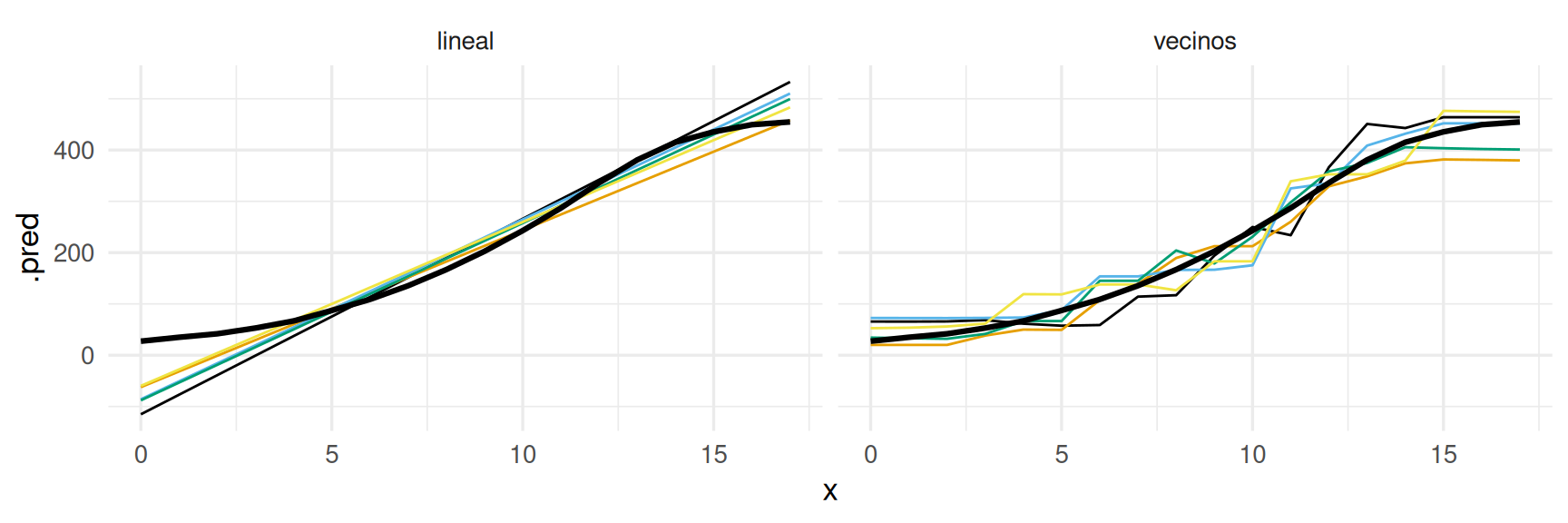

Esto patrón sugiere que, para las muestras que estamos considerando:

Nuestro método de vecinos más cercanos tiene capacidad para aprender patrones, pero tiene error considerable por sobreajuste.
Nuestro método lineal no varía mucho, pero tiene errores consistentes sobre todas las muestras. Su error se debe más a falta de capacidad o sesgo.

2.6 Diagnósticos básicos de sobreajuste y subajuste

Para que exista sobreajuste, la muestra debe poder empujar el algoritmo lejos del óptimo, en el esfuerzo por acercar los valores de la muestra de entrenamiento \(\hat{f}_{\mathcal L}(x^{(i)})\) a los respectivos \(y^{(i)}\). Por otro lado, cuando hay subajuste el algoritmo ajusta mal los valores observados en la muestra de entrenamiento.

Signos típicos de sobreajuste son:

El error de entrenamiento es considerablemente menor que el error de prueba. Aunque el error de entrenamiento es aceptable, el error de prueba es demasiado alto.
Los valores de \(\hat{f}_{\mathcal L}(\mathbf{x})\) dependen fuertemente de los valores individuales observados en la muestra de entrenamiento \(\mathcal{L}\) (lo cual idealmente no debería suceder, pues predicciones buenas no deberían cambiar mucho dependiendo de la muestra de entrenamiento).
Nuestro proceso \(\mathcal{L}\to \hat{f}_{\mathcal L}\) generalmente tiene un exceso de capacidad que permite al modelo aprender ruido en el conjunto de entrenamiento.
El tamaño de muestra de entrenamiento es relativamente chico (en relación con la complejidad del modelo).

Por otro lado, cuando existe subajuste,

El error de entrenamiento no es necesariamente lejano del error de prueba, y ambos son altos.
Los valores de \(\hat{f}_{\mathcal L}(\mathbf{x})\) son menos dependiendientes de los valores individuales observados en la muestra de entrenamiento \(\mathcal{L}\) (pues el modelo está cerca de saturar su capacidad, y no muy lejano a lo que obtendríamos con una muestra muy grande).
El proceso \(\mathcal{L}\to \hat{f}_{\mathcal L}\) tiene poca capacidad, y no puede aprender patrones claros y estables en los datos.
El tamaño de muestra de entrenamiento es relativamente grande (en relación con la complejidad del modelo).

Una algoritmo particular puede sufrir principalmente de sobreajuste o de subajuste, pero también puede sufrir de ambos problemas en distintas regiones del espacio de entradas donde queremos hacer predicciones.

Complejidad y error de predicción

Para un tamaño de muestra de entrenamiento fijo,

Métodos de predicción más flexibles o complejos tienden a sufrir más de sobreajuste, pues pueden sobreadaptarse fácilmente a datos observados.
Métodos de predicción más rígidos o simples tienden a sufrir más error por sesgo, pues tienen menos capacidad para aprender patrones.

Incrementar el tamaño de muestra generalmente mejora las predicciones, principalmente para algoritmos sobreajustados con muestra chica. Cuando el principal problema es subajuste, aumentar el tamaño de muestra puede ayudar menos.

2.7 Agregando más información y error irreducible

Podemos ver qué sucede cuando tenemos disponibles más variables relevantes. En este caso, probaremos con dos entradas:

genera_datos_2 <- function(n = 500, tipo = NULL){
  dat_tbl <- tibble(nse = runif(n, 0, 100)) |>
    mutate(estudio_años = floor(rnorm(n, 1.5 * sqrt(nse), 1))) |>
    mutate(estudio_años = pmax(0, pmin(17, estudio_años))) |> 
    mutate(habilidad = rnorm(n, 100 + 0.1 * nse, 1)) |> 
    mutate(z = 100 + (habilidad/100) * ( 20 * nse + 5 * (estudio_años))) |> 
    mutate(ingreso = pmax(0, 0.2*(z + rnorm(n, 0, 150))))
  obs_tbl <- dat_tbl |> 
    mutate(tipo = tipo, id = 1:n)
  obs_tbl |> select(id, tipo, x_1 = estudio_años, x_2 = nse,  y = ingreso)
}

entrena_tbl <- genera_datos_2(20, tipo = "entrena")
prueba_tbl <- genera_datos_2(500, tipo = "prueba")
receta_2 <- recipe(y ~ x_1 + x_2, data = entrena_tbl)
flujo_lineal <- workflow() |> 
  add_recipe(receta_2) |> 
  add_model(modelo_lineal)
# Ajustamos
flujo_ajustado_lineal <- fit(flujo_lineal, entrena_tbl)
predict(flujo_ajustado_lineal, bind_rows(entrena_tbl, prueba_tbl)) |> 
  bind_cols(bind_rows(entrena_tbl, prueba_tbl)) |>
  group_by(tipo) |> 
  rmse(truth = y, estimate = .pred) |> gt() |> 
  fmt_number(.estimate, decimals = 1)

tipo	.metric	.estimator	.estimate
entrena	rmse	standard	30.5
prueba	rmse	standard	37.0

Y vemos cómo inmediatamente redujimos el error de predicción: en este caso, aunque la variabilidad aumentó un poco (tenemos más parámetros que estimar vs el modelo con una sola variable), la reducción en el sesgo y en el error irreducible es tan grande que el desempeño es muy superior. Examina el caso de vecinos más cercanos.

2.8 Acerca de la estimación del error de predicción

Cuando usamos una muestra de prueba limitada, podemos evaluar la precisión de nuestra estimación del error de predicción usando por ejemplo el bootstrap. En nuestro ejemplo anterior podríamos hacer los siguiente:

library(infer)
preds <- predict(flujo_ajustado_lineal, bind_rows(prueba_tbl)) |> 
  bind_cols(prueba_tbl) 
preds |> 
  generate(reps = 1000, type = "bootstrap") |> 
  group_by(replicate, tipo) |> 
  rmse(truth = y, estimate = .pred) |> 
  select(replicate, tipo, stat = .estimate) |>
  get_ci(level = 0.90) |> 
  gt() |> fmt_number(where(is_double), decimals = 1)

lower_ci	upper_ci
35.1	38.6

2.9 Resumen

Tarea fundamental del análisis supervisado

Usando datos de entrenamiento \({\mathcal L}\), construimos una funcion \(\hat{f}\) para predecir. Estas funciones se ajustan usualmente intentando estimar directamente el predictor óptimo \(f^*(x)\) (si lo conocemos teóricamente), o indirectamente intentando minimizar la pérdida sobre el conjunto de entrenamiento.
Si observamos nuevos valores \(\mathbf{x}\), nuestra predicción es \(\hat{y} = \hat{f}(\mathbf{x})\).
Buscamos que cuando observemos nuevos casos para predecir, nuestro error de predicción sea bajo en promedio (\(Err\) sea bajo).
Usualmente estimamos \(Err\) mediante una muestra de prueba o validación \({\mathcal T}\).
Nos interesan métodos de construir \(\hat{f}\) que produzcan errores de predicción bajos.

Nótese que el error de entrenamiento se calcula sobre la muestra \({\mathcal L}\) que se usó para construir \(\hat{f}\), mientras que el error de predicción se estima usando una muestra independiente \({\mathcal T}\).
\(\hat{Err}\) es una estimación razonable de el error de predicción \(Err\) (por ejemplo, \(\hat{Err} \to Err\) cuando el tamaño de la muestra de prueba crece), pero \(\overline{err}\) típicamente es una estimación mala del error de predicción.
Nótese también que aunque generalmente podemos ajustar reduciendo el error de entrenamiento, lo que queremos es reducir el error de prueba: es decir, el error fuera de la muestra de entrenamiento.

Reduciendo el error de predicción

Para reducir el error de predicción, podemos:

Incluir variables relevantes que reduzcan el error irreducible
Reducir variabilidad usando métodos más estables o menos complejos
Reducir sesgo usando métodos más flexibles
Usar métodos con la estructura adecuada para el problema

Generalmente 2 y 3 están en contraposición, a lo que muchas veces se le llama equilibrio de varianza y sesgo. Los puntos 1 y 4 generalmente mejoran los resultados reduciendo tanto sesgo como variabilidad.

2.10 Muestras de validación y sobreajuste de prueba

Cuando probamos muchos métodos distintos, o varios profesionales intentan obtener buenas calificaciones en un conjunto de prueba, puede ser que aparezca sobreajuste al conjunto de prueba. Una manera de ver esto es que cuando hacemos una gran cantidad de intentos, y buscamos el mínimo error de prueba, es probable que los ganadores no generalizen tan bien a datos nuevos fuera de este conjunto de prueba, o dicho de otra forma, estamos de alguna manera usando los datos de prueba para entrenar. Adicionalmente, los métodos que utilizamos muchas veces tienen hiperparámetros que hay que afinar, lo que implica tener que hacer varias pruebas con datos fuera de los datos de entrenamiento (por ejemplo, un número apropiado de vecinos cercanos). Esto puede invalidar la estimación de error de prueba.

La solución para prevenir este sobreajuste es introducir una muestra de prueba adicional que llamamos muestra de validación. Por ejemplo, para un problema donde tenemos datos abundantes, podriamos dividir nuestros datos de la siguiente manera:

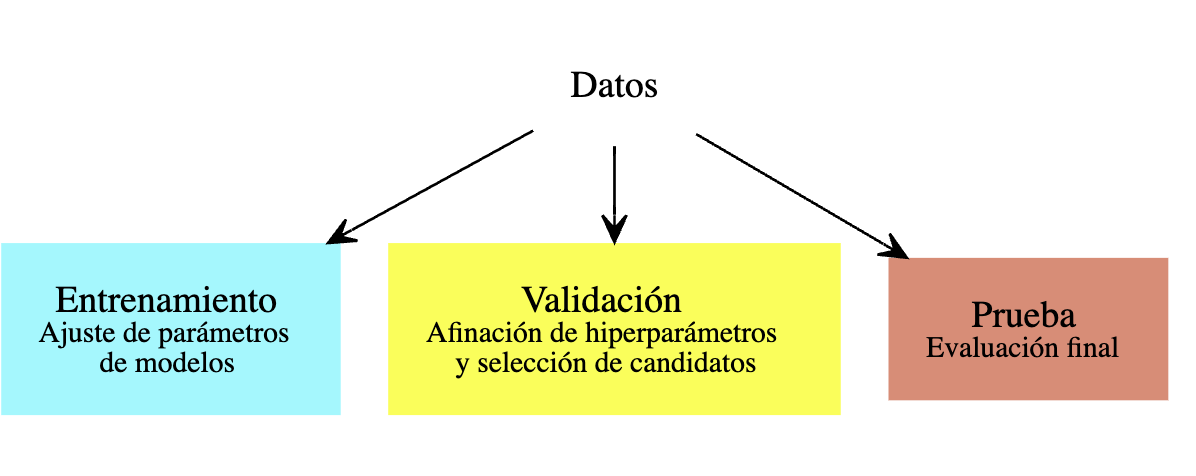
La razón de este proceso es que así podemos ir y venir entre entrenamiento y validación, buscando mejores enfoques y modelos, y no ponemos en riesgo la estimación final del error, o evaluación de calibración de intervalos o probabilidades. Por ejemplo, podemos dividir la muestra en 50-25-25 por ciento. Ajustamos modelos con el primer 50%, evaluamos y seleccionamos con el segundo 25% y finalmente, si es necesario, evaluamos el modelo final seleccionado con la muestra final de 25%.

El siguiente resumen explica las propiedades que requerimos en los distintos tipos de meustra:

Propiedades de entrenamiento-validación-prueba

No hay una regla general para decidir el tamaño del conjunto de entrenamiento. Generalmente conjuntos de datos más grandes y seleccionados apropiadamente dan mejores resultados.
Los conjuntos de validación y prueba deben ser preferentemente muestras aleatorias de las poblaciones para las que queremos hacer predicciones, para tener una estimación razonable (no sesgada por ejemplo) del desempeño futuro de nuestro modelo.
En cuanto a tamaño, en validación y prueba requerimos que sean de tamaño absoluto suficiente para tener una estimación con precisión suficientemente buena del error y del desempeño predictivo general de nuestros modelos (en el proceso de selección, con el conjunto de validación, y en la evaluación final, con el conjunto de prueba).
En validación y prueba, estamos haciendo una pregunta de inferencia: ¿de qué tamaño y bajo que diseño debe ser extraida la muestra de validación y prueba?

Nótese que en validación y prueba es donde la estadística es importante.

Por ejemplo: supongamos que hacemos un modelo para predecir impago. Quizá nuestro conjunto de entrenamiento tiene pocas personas de cierta región del país. Esto no quiere decir que no podamos aplicar nuestros métodos, siempre y cuando nuestra muesra de validación/prueba tenga suficientes ejemplos para asegurarnos de que nuestro desempeño no es malo en esas regiones (y por tanto produce resultados indeseables en la toma de decisiones).

Para decidir de antemano los tamaños de validación y prueba, tenemos que tener una idea de qué tanto varía el error de caso a caso (la varianza), si queremos hacer estimaciones en subgrupos de datos (que requerirán tamaño de muestra suficiente también), y cuánto es aceptable como error de estimación del desempeño predictivo, que generalmente no queremos que sea más del 25%, por ejemplo. En caso de usar muestras relativamente chicas de validación o prueba, es necesario estimar el error de estimación del desempeño.

2.11 Resolver problemas con aprendizaje automático

En este curso nos concentraremos en la construcción, evaluación y mejora de modelos predictivos. Para que estas ideas funcionen en problemas reales, hay más aspectos a considerar que no discutiremos con tanto detalle, pues en general están muy ligados al problema particular de predicción que nos interesa (y muchas veces son considerablemente más difíciles de la teoría y los algoritmos):

Para entender exactamente cuál es el problema que queremos resolver se requiere trabajo analítico considerable, y también trabajo en entender aspectos del área o negocio donde nos interesa usar aprendizaje máquina. Muchas veces es fácil resolver un problema muy preciso, que tenemos a la mano, pero que más adelante nos damos cuenta de que no es útil.
El punto anterior indentificar las métricas que queremos monitorear y mejorar, lo cual no siempre es claro. Hablaremos de este aspecto sólo desde un punto vista técnico. Optimizar métricas incorrectas es poco útil en el mejor de los casos, y en los peores pueden causar daños. Evitar esto requiere monitoreo constante de varios aspectos del funcionamiento de nuestros modelos y sus consecuencias.
¿Cómo poner en producción modelos y mantenerlos? Un flujo apropiado de trabajo, que comienza con pipelines de preproceso y heurísticas simples, para después utilizar modelos de aprendizaje automático, seguido de monitoreo y entrenamiento continuo son cruciales para tener éxito con este enfoque.